343. 整數拆分

給定一個正整數?n，將其拆分為至少兩個正整數的和，并使這些整數的乘積最大化。 返回你可以獲得的最大乘積。

示例 1:

• 輸入: 2
• 輸出: 1
• 解釋: 2 = 1 + 1, 1 × 1 = 1。

示例?2:

• 輸入: 10
• 輸出: 36
• 解釋: 10 = 3 + 3 + 4, 3 ×?3 ×?4 = 36。
• 說明: 你可以假設?n?不小于 2 且不大于 58。

本題需要注意的是，至少拆成2個正整數的和，而不是正好是2個正整數。

1. 確定dp數組以及下標的含義：dp[i]為整數i拆分后的最大乘積
2. 確定遞推公式：假如將i拆分為j和i-j，這里j不只是代表一個數字而是一可能由j個整數組成的乘積。如果從1遍歷到j，有兩種途徑可以得到dp[i]，一個是dp[i]=j*(i-j)，另一個是dp[i]=j*dp[i-j]，這里dp[i-j]代表i-j這個數字被拆分后的最大值。
3. dp數組如何初始化：本題將i拆成0是沒有意義的，所以不考慮，1拆開只能是1和0，也是沒有意義的，所以從2開始初始化，2可以拆成1 + 1，因此dp[2]=1
4. 確定遍歷順序：既然初始化是從2開始的，所以i從3開始遍歷，j從1開始遍歷，到i停止。
5. 舉例推導dp數組：沒法通過簡單計算舉例。

class Solution {public int integerBreak(int n) {int[] dp=new int[n+1]; dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=Math.max(dp[i], Math.max(j*dp[i-j], j*(i-j)));}}return dp[n];}
}

??本題的優化思路：其實將對于j的遍歷條件改為: j<i-1可以節省一步計算，因為如果讓j=i-1，其實在 j = 1的時候，這一步就已經拆出來了，屬于重復計算，所以 j < i - 1。

更優化一步，可以這樣：

for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}

因為拆分一個數i使之乘積最大，比如i=x+(i-x) dp[i]=x(i-x)=xi-x^2，這時是一個向下的拋物線，最大點為x/2

96.不同的叉搜索樹

給定一個整數 n，求以 1 ... n 為節點組成的二叉搜索樹有多少種？

示例:

這道題要求能構造多少二叉搜索樹。二叉搜索樹是有一定規律的，其中序遍歷是有序的。按照示例所給，可以先從1開始遍歷，看以i為根節點能構造出多少子樹。其實一開始還是沒有什么思路，主要是遞推公式不太好想，所以準備按照五部曲依次思考一下：

1. 確定dp數組以及下標的含義：dp[i]為有i個節點時能構造的二叉搜索樹個數。
2. 確定遞推公式：目前還沒有什么思路。
3. dp數組如何初始化：若n=1，則dp[1]毫無疑問是1，若n=2，則有兩種構造方法，一種是以1為根節點，左子樹為空，右子樹為2；一種是以2為根節點，左子樹為1，右子樹為空，所以dp[2]=2；n=3就是示例中所給情況，可以看到，如果以1為根節點，則左子樹一定為空的，右子樹有兩種可能，分別是以2和3為子樹根節點。若以2為根節點，則左右子樹各有一個節點，有一種可能，若以3為根節點，則右子樹為空，左子樹有兩種可能，分別是以1和2為子樹根節點。

當分析到如何初始化的時候，已經漸漸有了關于推導遞推公式的雛形，接下來可以捋一下思路：

當n=1時：只有一個節點，不附圖了

當n=2時：如下

當n=3時，有三種大的情況：

1. 以1為根節點：因為此題本質求的是樹的形狀的可能性，所以跟具體的數值關系不大，如果把1去掉來看，可以看到，其實剩下的形狀和n=2的時候是一樣的：
2. 以2為根節點：左邊節點1，右邊節點3
3. 以3為根節點：去掉3，剩下的形狀和n=2的時候也是一樣的：

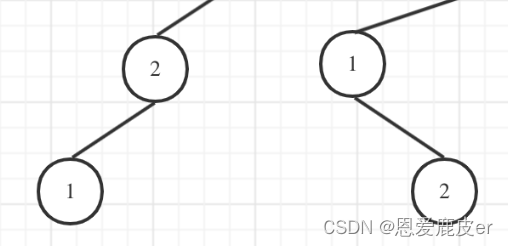
因此

• 有2個元素的搜索樹數量就是dp[2]。
• 有1個元素的搜索樹數量就是dp[1]。
• 有0個元素的搜索樹數量就是dp[0]。

可以這樣推導：

1. 以1為頭節點的搜索樹個數=右子樹有2個元素搜索樹數量*左子樹有0個元素搜索樹數量
2. 以2為頭節點的搜索樹個數=右子樹有1個元素搜索樹數量*左子樹有1個元素搜索樹數量
3. 以3為頭節點的搜索樹個數=右子樹有0個元素搜索樹數量*左子樹有2個元素搜索樹數量

那么n=3時，dp[3]就是上面三種情況的搜索樹個數之和，即dp[3]=dp[2]*dp[0]+dp[1]*dp[1]+dp[0]*dp[2] ，

拓展到i就是：不斷地累加：dp[以j為頭結點左子樹節點數量]*dp[以j為頭結點右子樹節點數量]，j的范圍為[1, i]

所以遞推公式為：dp[i]+=dp[j-1]*dp[i-j]，因此下面完整的五部曲為：

1. 確定dp數組以及下標的含義：有i個節點時能構造的二叉搜索樹個數
2. 確定遞推公式：dp[i]+=dp[j-1]*dp[i-j]
3. dp數組如何初始化：要注意，從定義上來講，空節點也是一棵二叉樹，也是一棵二叉搜索樹，所以dp[0]=1，這個我一開始弄錯了。dp[1]=1
4. 確定遍歷順序：i從1到n，j從1到i
5. 舉例推導dp數組：無法手動舉更多例子

class Solution {/**確定dp數組以及下標的含義：有i個節點時能構造的二叉搜索樹個數確定遞推公式：dp[i]+=dp[j-1]*dp[i-j]dp數組如何初始化：dp[1]=1，dp[2]=2確定遍歷順序：i從3到n，j從1到i*/public int numTrees(int n) {int[] dp=new int[n+1];dp[0]=1;dp[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
}