分位數回歸的長短期神經記憶網絡介紹：
QRLSTM（Quantile Regression Long Short-Term Memory）分位數回歸神經網絡是一種結合了長短期記憶（LSTM）神經網絡和分位數回歸的模型。這種神經網絡結構旨在對數據的不同分位數進行回歸預測，而不僅僅是預測均值。分位數回歸的長短期記憶神經網絡結合了LSTM的序列建模能力和分位數回歸的非參數特性，可以更全面地了解數據的分布情況，在金融領域、氣象預測等需要對不確定性進行建模的領域有著廣泛的應用。
通過訓練QRLSTM模型，可以得到不同分位數下的預測結果，從而更好地理解數據的分布情況，并能夠提供更全面的風險評估和決策支持。
分位數回歸根據是不同分位數下自變量的變化情況，以便于更好的根據不同分位點下的信息進行分析解釋。當我們不僅希望研究響應變量的期望均值，而且希望能探索響應 變量的全局分布，普通的線性回歸就不再起作用，這時候就需要分位數回歸了。1978年 Koenker和Bassett提出了分位數回歸的概念，彌補了最小二乘法估計存在的缺陷，處理了其在有離群值、多峰值的樣本的擬合，解決了最小二乘法完成無法比如異方差、尖峰等多種問題數據的分析的相關問題，可以描述響應變量的全局特征，可以挖掘到更為豐富的信息，另外分位數回歸估計采用的是加權的最小絕對離差和（weighted lest absolute deviation，WLAD）法進行穩健估計，使得存在誤差的模型上的估計方法依舊可以使用。 許啟發等提出了一種改進的分位數，這種改進后的條件分位數和傳統的均值回歸方法相比能夠大幅提高預測的精確度。事實上，均值回歸是特殊的分位數回歸，就是分為點為 0.5的情況，所以改進后的條件分位數除了這一點還有很多分位點，可以更好地描繪負荷在不同分位點的分布情況，且該方法還能推廣延伸到條件概率分布，是非參數統計方法之一。

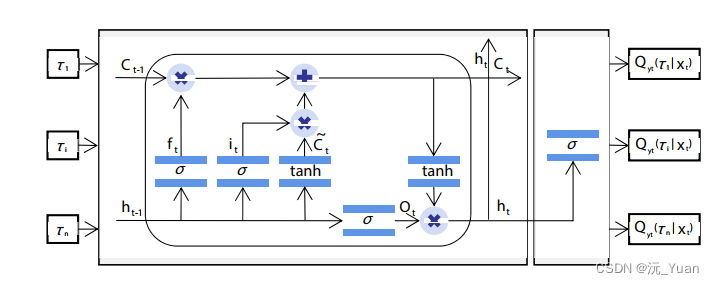
圖源來自論文：A hybrid carbon price prediction model based-combinational estimation strategies of quantile regression and long short-term memory
QRLSTM網絡搭建：

%   for i = 0.05:0.15:0.95 % 90%置信區間layers = [sequenceInputLayer([L, 1, 1], "Name", "sequence")                 % 建立輸入層，輸入數據結構為[f_, 1, 1]flattenLayer("Name", "flatten")                                    % 網絡鋪平層lstmLayer(lstmnumber,'Name','lstm1',"OutputMode", "last")                    % lstm層fullyConnectedLayer(1, "Name", "fc")                               % 全連接層quanRegressionLayer('out',i)];                      % 分位數回歸層%%  參數設置
options = trainingOptions('adam', ...      % Adam 梯度下降算法'MaxEpochs', 100, ...                 % 最大迭代次數'InitialLearnRate', 1e-2, ...          % 初始學習率為0.01'LearnRateSchedule', 'piecewise', ...  % 學習率下降'LearnRateDropFactor', 0.1, ...        % 學習率下降因子 0.1'LearnRateDropPeriod', 90, ...        % 經過90次訓練后 學習率為 0.01 * 0.1'Shuffle', 'every-epoch', ...          % 每次訓練打亂數據集'Verbose', 1);

訓練結果：



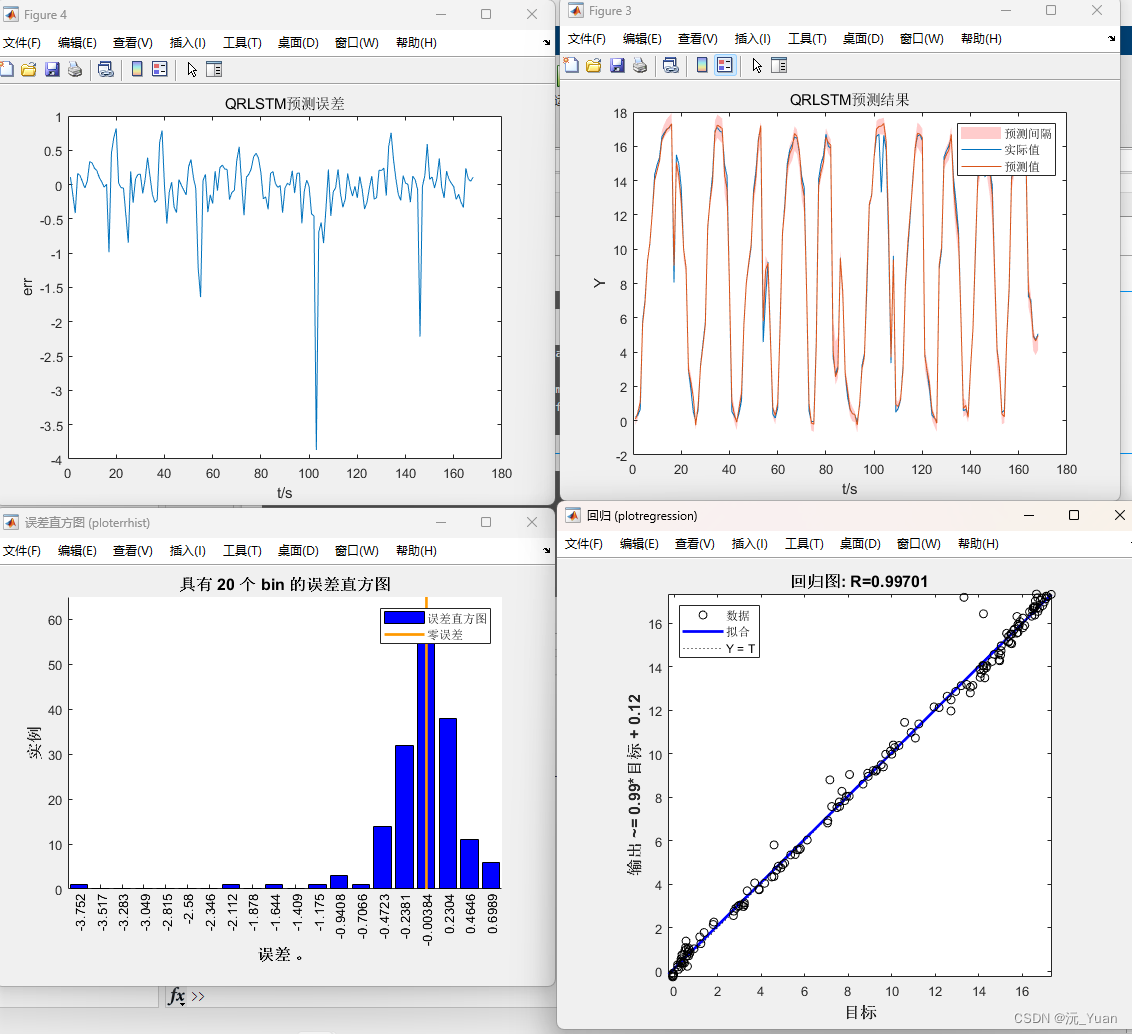
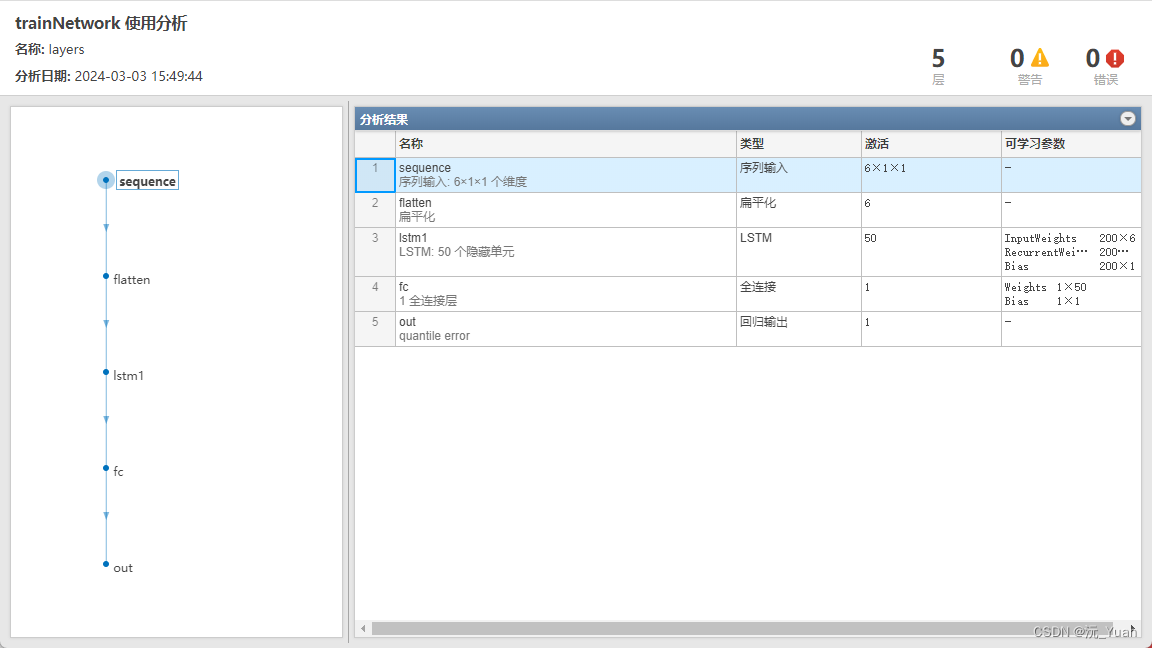
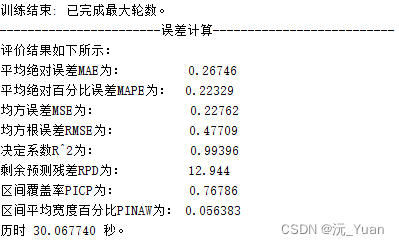
完整代碼獲取：QRLSTM代碼