系列文章目錄

代碼隨想錄算法訓練營第一天|數組理論基礎，704. 二分查找，27. 移除元素
代碼隨想錄算法訓練營第二天|977.有序數組的平方 ，209.長度最小的子數組 ，59.螺旋矩陣II
代碼隨想錄算法訓練營第三天|鏈表理論基礎，203.移除鏈表元素，707.設計鏈表，206.反轉鏈表
代碼隨想錄算法訓練營第四天|24. 兩兩交換鏈表中的節點，19.刪除鏈表的倒數第N個節點，面試題 02.07. 鏈表相交，142.環形鏈表II，總結
代碼隨想錄算法訓練營第五天|哈希表理論基礎，242.有效的字母異位詞，349. 兩個數組的交集，202. 快樂數，1. 兩數之和
代碼隨想錄算法訓練營第六天|454.四數相加II，383. 贖金信，15. 三數之和，18. 四數之和，總結
代碼隨想錄算法訓練營第七天|344.反轉字符串，541. 反轉字符串II，卡碼網：54.替換數字，151.翻轉字符串里的單詞，卡碼網：55.右旋轉字符串
代碼隨想錄算法訓練營第八天|28. 實現 strStr()，459.重復的子字符串，字符串總結，雙指針回顧
代碼隨想錄算法訓練營第九天|理論基礎，232.用棧實現隊列，225. 用隊列實現棧
代碼隨想錄算法訓練營第十天|20. 有效的括號，1047. 刪除字符串中的所有相鄰重復項，150. 逆波蘭表達式求值
代碼隨想錄算法訓練營第十一天|239. 滑動窗口最大值，347.前 K 個高頻元素，總結
代碼隨想錄算法訓練營第十二天|理論基礎，遞歸遍歷，迭代遍歷，統一迭代
代碼隨想錄算法訓練營第十三天|層序遍歷10，226.翻轉二叉樹，101.對稱二叉樹
代碼隨想錄算法訓練營第十四天|104.二叉樹的最大深度，559.n叉樹的最大深度，111.二叉樹的最小深度，222.完全二叉樹的節點個數
代碼隨想錄算法訓練營第十五天|110.平衡二叉樹，257. 二叉樹的所有路徑，404.左葉子之和
代碼隨想錄算法訓練營第十六天|513.找樹左下角的值，112. 路徑總和，113.路徑總和ii，106.從中序與后序遍歷序列構造二叉樹，105.從前序與中序遍歷序列構造二叉樹
代碼隨想錄算法訓練營第十七天|654.最大二叉樹，617.合并二叉樹，700.二叉搜索樹中的搜索，98.驗證二叉搜索樹
代碼隨想錄算法訓練營第十八天|530.二叉搜索樹的最小絕對差，501.二叉搜索樹中的眾數，236. 二叉樹的最近公共祖先
代碼隨想錄算法訓練營第十九天|235. 二叉搜索樹的最近公共祖先，701.二叉搜索樹中的插入操作，450.刪除二叉搜索樹中的節點
代碼隨想錄算法訓練營第二十天|669. 修剪二叉搜索樹，108.將有序數組轉換為二叉搜索樹，538.把二叉搜索樹轉換為累加樹，總結篇
代碼隨想錄算法訓練營第二十一天|回溯算法理論基礎，77. 組合
代碼隨想錄算法訓練營第二十二天|216.組合總和III，17.電話號碼的字母組合
代碼隨想錄算法訓練營第二十三天|39. 組合總和，40.組合總和II，131.分割回文串
代碼隨想錄算法訓練營第二十四天|93.復原IP地址，78.子集，90.子集II
代碼隨想錄算法訓練營第二十五天|491.遞增子序列，46.全排列，47.全排列 II
代碼隨想錄算法訓練營第二十六天|332.重新安排行程，51. N皇后，37. 解數獨，總結
代碼隨想錄算法訓練營第二十七天|貪心算法理論基礎，455.分發餅干，376. 擺動序列，53. 最大子序和
代碼隨想錄算法訓練營第二十八天|122.買賣股票的最佳時機II，55. 跳躍游戲，45.跳躍游戲II
代碼隨想錄算法訓練營第二十九天|1005.K次取反后最大化的數組和，134. 加油站，135. 分發糖果
代碼隨想錄算法訓練營第三十天|860.檸檬水找零，406.根據身高重建隊列，452. 用最少數量的箭引爆氣球
代碼隨想錄算法訓練營第三十一天|435. 無重疊區間，763.劃分字母區間，56. 合并區間
代碼隨想錄算法訓練營第三十二天|738.單調遞增的數字，968.監控二叉樹，總結
代碼隨想錄算法訓練營第三十三天|動態規劃理論基礎，509. 斐波那契數，70. 爬樓梯，746. 使用最小花費爬樓梯
代碼隨想錄算法訓練營第三十四天|62.不同路徑，63. 不同路徑 II
代碼隨想錄算法訓練營第三十五天|343. 整數拆分，96.不同的二叉搜索樹
代碼隨想錄算法訓練營第三十六天|背包理論基礎，416. 分割等和子集
代碼隨想錄算法訓練營第三十七天|1049. 最后一塊石頭的重量 II，494. 目標和，474.一和零
代碼隨想錄算法訓練營第三十八天|完全背包，518. 零錢兌換 II，377. 組合總和 Ⅳ
代碼隨想錄算法訓練營第三十九天|70. 爬樓梯 （進階），322. 零錢兌換，279.完全平方數
代碼隨想錄算法訓練營第四十天|139.單詞拆分，多重背包介紹，背包問題總結篇！

---

198.打家劫舍

題目鏈接： 198.打家劫舍
題目內容： 你是一個專業的小偷，計劃偷竊沿街的房屋。每間房內都藏有一定的現金，影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警。給定一個代表每個房屋存放金額的非負整數數組，計算你 不觸動警報裝置的情況下 ，一夜之內能夠偷竊到的最高金額。
視頻講解： 動態規劃，偷不偷這個房間呢？| LeetCode：198.打家劫舍

動態規劃問題的五步曲：

• 確定dp數組（dp table）以及下標的含義：考慮下標i（包括i）以內的房屋，最多可以偷竊的金額為dp[i]

• 確定遞推公式：dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])

• dp數組如何初始化：dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1])

• 確定遍歷順序：從前到后遍歷

• 舉例推導dp數組

class Solution:def rob(self, nums: List[int]) -> int:if len(nums) == 0:return 0if len(nums) == 1:return nums[0]dp=[0]*len(nums)dp[0]=nums[0]dp[1]=max(nums[0],nums[1])for i in range(2,len(nums)):dp[i]=max(dp[i-1],dp[i-2]+nums[i])return dp[-1]

213.打家劫舍II

題目鏈接： 213.打家劫舍II
題目內容： 你是一個專業的小偷，計劃偷竊沿街的房屋，每間房內都藏有一定的現金。這個地方所有的房屋都 圍成一圈 ，這意味著第一個房屋和最后一個房屋是緊挨著的。同時，相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警 。給定一個代表每個房屋存放金額的非負整數數組，計算你 在不觸動警報裝置的情況下 ，今晚能夠偷竊到的最高金額。
視頻講解： 動態規劃，房間連成環了那還偷不偷呢？| LeetCode：213.打家劫舍II

與打家劫舍1的區別：打家劫舍II中的房屋連成環了，第一個房屋和最后一個房屋是緊挨著的。
對于一個數組，成環的話主要有如下三種情況：

• 情況一：考慮不包含首尾元素
• 情況二：考慮包含首元素，不包含尾元素
• 情況三：考慮包含尾元素，不包含首元素

而情況二 和 情況三 都包含了情況一了，所以只考慮情況二和情況三就可以了。

動態規劃問題的五步曲：

• 確定dp數組（dp table）以及下標的含義：爬到有i個臺階的樓頂，有dp[i]種方法

• 確定遞推公式：dp[i] += dp[i - j]

• dp數組如何初始化：dp[0] = 1，下標非0的dp[j]初始化為0

• 確定遍歷順序：這是背包里求排列問題，即：1、2 步 和 2、1 步都是上三個臺階，但是這兩種方法不一樣！所以需將target放在外循環，將nums放在內循環。每一步可以走多次，這是完全背包，內循環需要從前向后遍歷。

• 舉例推導dp數組

class Solution:def rob(self, nums: List[int]) -> int:if len(nums)==0:return 0if len(nums)==1:return nums[0]#情況二result1=self.robRange(nums,0,len(nums)-2)#情況三result2=self.robRange(nums,1,len(nums)-1)return max(result1,result2)def robRange(self,nums,start,end):if end==start:return nums[start]#初始化prev_max=nums[start] curr_max=max(nums[start],nums[start+1])for i in range(start+2,end+1):temp=curr_maxcurr_max=max(prev_max+nums[i],curr_max)prev_max=tempreturn curr_max

337.打家劫舍III

題目鏈接： 337.打家劫舍III
題目內容： 小偷又發現了一個新的可行竊的地區。這個地區只有一個入口，我們稱之為 root 。除了 root 之外，每棟房子有且只有一個“父“房子與之相連。一番偵察之后，聰明的小偷意識到“這個地方的所有房屋的排列類似于一棵二叉樹”。 如果 兩個直接相連的房子在同一天晚上被打劫 ，房屋將自動報警。給定二叉樹的 root 。返回 在不觸動警報的情況下 ，小偷能夠盜取的最高金額 。
視頻講解： 動態規劃，房間連成樹了，偷不偷呢？| LeetCode：337.打家劫舍3

動態規劃其實就是使用狀態轉移容器來記錄狀態的變化，這里可以使用一個長度為2的數組，記錄當前節點偷與不偷所得到的的最大金錢。

遞歸三部曲：

• 確定遞歸函數的參數和返回值：要求一個節點 偷與不偷的兩個狀態所得到的金錢，那么參數為當前節點，返回值就是一個長度為2的數組。這里的返回數組就是dp數組。

dp數組（dp table）以及下標的含義：下標為0記錄不偷該節點所得到的的最大金錢，下標為1記錄偷該節點所得到的的最大金錢。所以本題dp數組就是一個長度為2的數組！（在遞歸的過程中，系統棧會保存每一層遞歸的參數）

• 確定終止條件：在遍歷的過程中，如果遇到空節點的話，很明顯，無論偷還是不偷都是0，所以就返回[0,0]（這也相當于dp數組的初始化）
• 確定遍歷順序：后序遍歷。因為要通過遞歸函數的返回值來做下一步計算。
  通過遞歸左節點，得到左節點偷與不偷的金錢。
  通過遞歸右節點，得到右節點偷與不偷的金錢。
• 確定單層遞歸的邏輯：
  • 如果是偷當前節點，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]
  • 如果不偷當前節點，那么左右孩子就可以偷，至于到底偷不偷一定是選一個最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1])
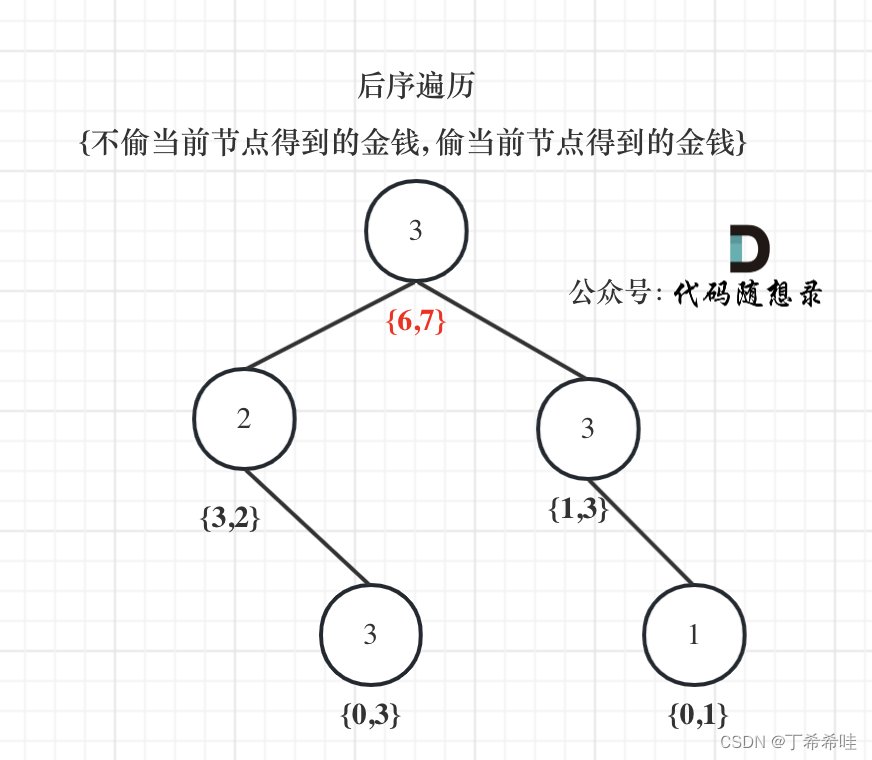
  • 最后當前節點的狀態就是{val2, val1}; 即：{不偷當前節點得到的最大金錢，偷當前節點得到的最大金錢}
• 舉例推導dp數組

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:dp=self.traversal(root)return max(dp)def traversal(self,node):#遞歸終止條件if not node:return (0,0)#左節點left=self.traversal(node.left)#右節點right=self.traversal(node.right)#不偷當前節點var1=max(left[0],left[1])+max(right[0],right[1])#偷當前節點var2=node.val+left[0]+right[0]return (var1,var2)