前綴和算法題（區間次方和、小藍平衡和、大石頭的搬運工、最大數組和）

一、前綴和的原理和特點

prefix表示前綴和，前綴和由一個用戶輸入的數組生成。對于一個數組a[]（下標從1開始），我們定義一個前綴和數組prefix[]，滿足：

prefix有一個重要的特性，可以用于快速生成prefix:

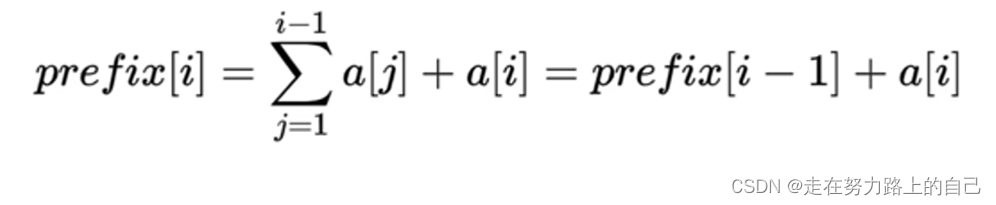
prefix可以O(1)的求數組a[]的一段區間的和:

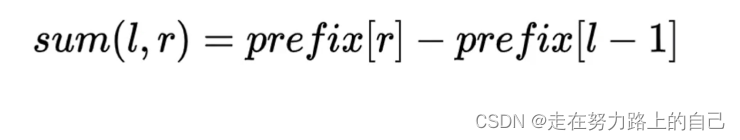
但是注意，prefix是一種預處理算法，只適用于a數組為靜態數組的情況，即a數組中的元素在區間和查詢過程中不會進行修改。

如果需要實現“先區間修改，再區間查詢”可以使用差分數組，如果需要“一邊修改，一邊查詢”需要使用樹狀數組或線段樹等數據結構。

二、實現前綴和

利用前面講過的特性:prefix[i]= prefix[i - 1] + a[i]我們的數組下標均從1開始，a[0]=0，從前往后循環計算即可。

for(int i = 1;i <= n; ++ i)
prefix[i]= prefix[i - 1] + a[i];

求區間和:
sum(L, R) = prefix[R]-prefix[L - 1]

三、例題

（一、區間次方和）

用戶登錄

問題描述
給定一個長度為 n 的整數數組 a 以及 m 個查詢。
每個查詢包含三個整數 l,r,k 表示詢問 l~r ,之間所有元素的 k 次方和。
請對每個查詢輸出一個答案，答案對 1e9+7取模。
輸入格式
第一行輸入兩個整數 n,m 其含義如上所述。
第二行輸入 n 個整數 a[1], a[2],…, a[n]。
接下來 m 行，每行輸入三個整數 l,r,k 表示一個查詢。
輸出格式
輸出 m 行，每行一個整數，表示查詢的答案對 1e9+7 取模的結果。

由于k比較小，所以我們可以處理出五個數組分別表示不同的次方，例如a[3][]中的元素都是數組a中元素的3次方。再對五個數組預處理出前綴和，對于每次詢問利用前綴和的性質可O(1)解決。

#define  _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>using namespace std;using ll = long long;
const ll p = 1e9 + 7;
const int N = 1e5 + 9;
ll a[6][N], prefix[6][N];
// 設置a[6]的原因:
// 由于 k 較小(1 ~ 5), 可以直接計算各個數的 1 ~ k次方int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n, m; cin >> n >> m;// 輸入兩個整數 n,m // n 表示 a[] 數組中有 n 個元素for (int i = 1; i <= n; ++i)cin >> a[1][i]; // 輸入 n 個整數for (int i = 2; i <= 5; ++i)for (int j = 1; j <= n; ++j)a[i][j] = a[i - 1][j] * a[1][j] % p;// 求 a[]各個數的 1 ~ 5的次方和for (int i = 1; i <= 5; ++i)for (int j = 1; j <= n; ++j)prefix[i][j] = (prefix[i][j - 1] + a[i][j]) % p;// 求 a[j] 的前綴和取余while (m--){int l, r, k; cin >> l >> r >> k;cout << (prefix[k][r] - prefix[k][l - 1] + p) % p << '\n';// 求數組a[]的(l, r)的和:}return 0;
}

（二、小藍平衡和）

問題描述
平衡串指的是一個字符串，其中包含兩種不同字符，并且這兩種字符的數量相等。
例如，ababab和 aababb 都是平衡串，因為每種字符各有三個，而 ababab和 aaaab 都不是平衡串，因為它們的字符數量不相等。
平衡串在密碼學和計算機科學中具有重要應用，比如可以用于構造哈希函數或者解決一些數學問題。
小鄭拿到一個只包含 L、Q 的字符串，他的任務就是找到最長平衡串，且滿足平衡串的要求，即保證子串中 L、Q 的數量相等。
輸入格式
輸入一行字符串，保證字符串中只包含字符 L、Q.
輸出格式
輸出一個整數，為輸入字符串中最長平衡串的長度。

將L看做1，Q看做-1，只有當某個區間的和為0時，字符串是平衡的。
我們可以預處理出前綴和，然后枚舉所有區間(這一步的時間復雜度是O(n^2)的)，得到所有平衡區間的長度最后取大輸出即可。

#define  _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>using namespace std;
const int N = 1010;char s[N];int prefix[N];int main()
{cin >> s + 1;// 從數組s的第2個位置開始讀取字符串（即跳過s[0]），這樣字符串的下標就從1開始了  int n = strlen(s + 1);// 計算字符串的長度(從 s[1] 開始計算)for (int i = 1; i <= n; ++i)prefix[i] = prefix[i - 1] + (s[i] == 'L' ? 1 : -1);// 求各個 (1, i) 的前綴和, 如果是 'L' 則加一int ans = 0;for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j)// 遍歷所有可能出現平衡串的串if (prefix[j] - prefix[i - 1] == 0)ans = max(ans, j - i + 1);// 得到最大值		cout << ans << '\n';return 0;
}

（三、大石頭的搬運工）

用戶登錄

問題描述
在一款名為”大石頭的搬運工“的游戲中，玩家需要操作一排 n 堆石頭，進行n -1輪游戲。
每一輪，玩家可以選擇一堆石頭，并將其移動到任意位置。
在n-1輪移動結束時，要求將所有的石頭移動到一起(即所有石頭的位置相同)即為成功。
移動的費用為石頭的重量乘以移動的距離。例如，如果一堆重量為2 的石頭從位置 3 移動到位置 5，那么費用為 2 x(5 -3)= 4。
請計算出所有合法方案中，將所有石頭移動到一起的最小費用。
可能有多堆石頭在同一個位置上，但是一輪只能選擇移動其中一堆。
輸入格式
第一行一個整數 n，表示石頭的數量。
接下來幾行，每行兩個整數 w;和pi，分別表示第之個石頭的重量和初始位置。
輸出格式
輸出一個整數，表示最小的總移動費用。

解法一：

#include <bits/stdc++.h>
// 包含所有標準庫// 絕對值表達式 |x-1| + |x-2| + |x-6| + |x-13| 取最小值時，x取中位數時最小。
// 在一組石頭"坐標-重量"對應的情況下，找到一個位置x，使得移動所有石頭到這個位置的總成本最小（成本定義為每個石頭的重量乘以其到x的距離）。using Pair = std::pair<int, int>;
// Pair類型用來存儲石頭的重量和初始位置using LL = long long; // 長整型，用來處理可能的大數字void solve(const int& Case) {int n; std::cin >> n; // n是石頭的數量std::vector<Pair> a(n); // Pair的向量，存儲石頭的重量和初始位置LL sw = 0; // sw是所有石頭的總重量for (auto& [w, p] : a) std::cin >> w >> p, sw += w; // 輸入每個石頭的重量和位置，并更新總重量swstd::sort(a.begin(), a.end()); // 按石頭的位置進行排序LL nw = 0; // nw是當前處理過的石頭的總重量int x = 0; // x是使得總成本最小的位置// 遍歷排序后的石頭，尋找滿足nw * 2 < sw <= nw + w * 2的xfor (const auto& [w, p] : a) {if (nw * 2 < sw && sw <= (nw + w) * 2) {x = p; // 當前位置p是滿足條件的xbreak;}nw += w; // 更新當前處理過的石頭的總重量nw}LL ans = 0; // 總成本for (const auto& [w, p] : a) {ans += (LL)w * std::abs(p - x); // 計算每個石頭移動到x的成本并累加到ans}std::cout << ans << '\n'; // 輸出總成本
}int main() {std::ios::sync_with_stdio(false); // 同步標準C++和C的流，通常可以加速輸入輸出std::cin.tie(nullptr); // 解綁cin和cout的綁定，通常可以加速輸入輸出std::cout.tie(nullptr);int T = 1; // 測試用例的數量，默認為1for (int i = 1; i <= T; ++i) solve(i); // 處理每一個測試用例return 0;
}

?解法二：

解題思路

首先，我們需要明白在這個問題中，每一次移動的石頭的位置并不影響后續的移動，也就是說，無論我們怎么移動石頭，最后的總費用只依賴于每個石頭最后的位置，而與移動的順序無關。這個性質使得我們可以逐一考慮每個石頭最后的位置，并比較得出最小的總費用。

然后，我們需要分析一下如何計算每一種放置石頭的方式的總費用。一種直觀的方法是，對于每個石頭，我們都計算它被移動到目標位置的費用，然后將這些費用加總。但這樣的計算方式在本題的數據范圍下是無法接受的。我們需要尋找一種更優的方法。

這里，我們可以運用前綴和的思想。考慮到石頭移動的費用與其重量和距離有關，我們可以先將石頭按位置排序，然后計算每個石頭移動到任一位置的費用，再利用前綴和的方法將這些費用累加起來。具體地，我們可以定義兩個數組 pre?和?nex，其中?pre[i]?表示前?i?個石頭都移動到第?i?個石頭的位置的總費用，nex[i]?表示第?i?個石頭之后的所有石頭都移動到第?i?個石頭的位置的總費用。這樣，對于每個石頭，我們就可以在?O(1)?的時間內算出所有石頭都移動到它的位置的總費用。

時間復雜度分析

整個過程中，排序的時間復雜度是?O(nlogn)，計算 pre?和?nex?的時間復雜度是 O(n)，查找 pre+nex?的最小值的時間復雜度是 O(n)，所以總的時間復雜度是 O(nlogn)。

#include <iostream>
#include <cstring>
#include <algorithm>#define x first // 簡化pair中位置的訪問
#define y second // 簡化pair中重量的訪問using namespace std;typedef long long LL;
typedef pair<int, int> PII; 
// pair類型用來存儲石頭的重量和初始位置 const int N = 1e5 + 10;int n; // n, 表示石頭的數量
PII q[N]; // 存儲每個石頭的位置和重量的數組
LL pre[N], nex[N];// 前綴和數組,后綴和數組int main()
{cin >> n; // n, 表示石頭的數量for (int i = 1; i <= n; ++i)cin >> q[i].y >> q[i].x;// 輸入 重量 w 和 初始位置 psort(q + 1, q + n + 1);// 按石頭的位置進行排序LL s = 0; // 統計總重量for (int i = 1; i <= n; ++i){pre[i] = pre[i - 1]; // 計算當前石頭前的總成本pre[i] += s * (q[i].x - q[i - 1].x);// 累加前綴和s += q[i].y;// 更新總重量}s = 0; // 重置總重量, 用于計算后綴和for (int i = n; i >= 1; --i){nex[i] = nex[i + 1]; // 計算當前石頭后的總成本nex[i] += s * (q[i + 1].x - q[i].x);// 累加后綴和s += q[i].y;// 更新總重量}LL res = 1e18;for (int i = 1; i <= n; ++i)res = min(res, pre[i] + nex[i]);// 找到移動所有石頭的最小總成本cout << res << endl;return 0;
}

（四、最大數組和）

用戶登錄

問題描述
小明是一名勇敢的冒險家，他在一次探險途中發現了一組神秘的寶石，這些寶石的價值都不同。但是，他發現這些寶石會隨著時間的推移逐漸失去價值，因此他必須在規定的次數內對它們進行處理。
小明想要最大化這些寶石的總價值。他有兩種處理方式
1.選出兩個最小的寶石，并將它們從寶石組中刪除。
2.選出最大的寶石，并將其從寶石組中刪除。
現在，給你小明手上的寶石組，請你告訴他在規定的次數內，最大化寶石的總價值是多少。
輸入格式
第一行包含一個整數 t，表示數據組數。
對于每組數據，第一行包含兩個整數幾和ん，表示寶石的數量和規定的處理次數。
第二行包含 n 個整數 a1,a2,…., an，表示每個寶石的價值。
輸出格式
對于每組數據，輸出一個整數，表示在規定的次數內，最大化寶石的總價值。

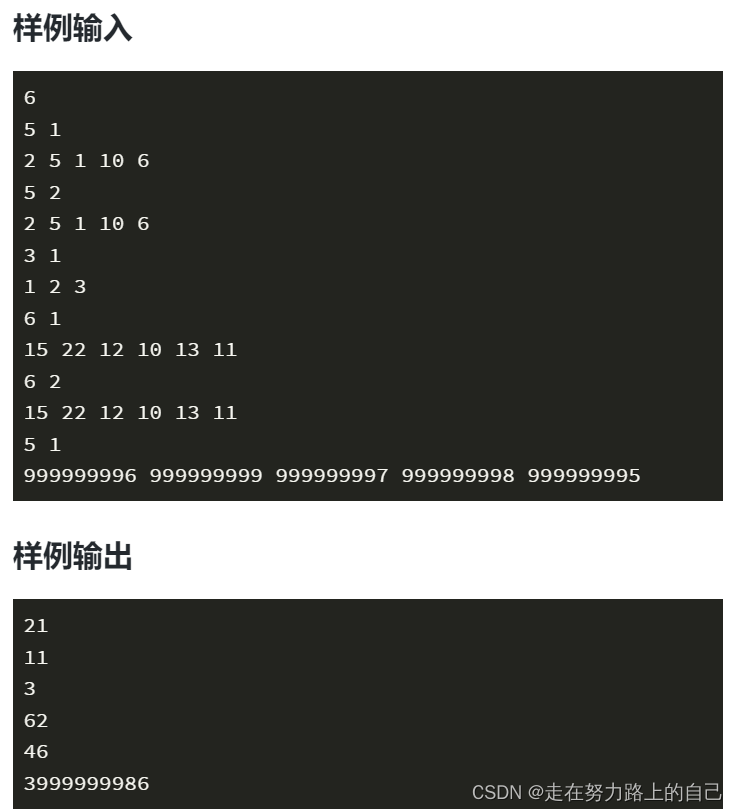
樣例輸入：

6 5 1 2 5 1 10 6 5 2 2 5 1 10 6 3 1 1 2 3 6 1 15 22 12 10 13 11 6 2 15 22 12 10 13 11 5 1 999999996 999999999 999999997 999999998 999999995

樣例輸出：

21 11 3 62 46 3999999986?

解法一：

解題思路

首先，我們想到了一種貪心的解法，每次刪除價值和更小的兩個寶石或者刪除價值最大的寶石，根據哪種操作可以刪除價值更小的寶石。然而，這種方法甚至在示例上都不適用，我們需要更優的解法。

注意到操作的順序并不重要：刪除兩個最小的寶石然后再刪除最大的寶石與先刪除最大的寶石然后再刪除兩個最小的寶石的操作是相同的。因此，我們可以假設刪除了最小兩個寶石的操作次數為?𝑚m，當我們刪除兩個最小的寶石時，剩下的寶石組成的數組就是從中刪除了?2𝑚2m?個最小寶石和?(𝑘?𝑚)(k?m)?個最大寶石的寶石數組。

如何快速計算剩余元素的總和？首先，對原始數組進行排序不會影響結果，因為最小寶石始終在數組的開頭，最大寶石則在數組的末尾。也就是排序后，每次操作要么刪除左邊的兩個元素，要么刪除右邊的一個元素。因此，如果我們刪除?2𝑚?個最小寶石和?(𝑘?𝑚) 個最大寶石，則剩余的元素組成的段在排序后的數組中從位置?(2𝑚+1) 到位置?(𝑛?(𝑘?𝑚)) ，可以從左到右遍歷?m，使用前綴和在 O(1)?時間內計算其總和。總的時間復雜度 O(k)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{int t;cin >> t;// 輸入整數 t, 表示數據組數while (t--) {int n, k;cin >> n >> k;// 輸入 n, 表示寶石的數量// 輸入 k, 表示規定的處理次數vector<ll> a(n), prefix(n + 1, 0);// 數組 a 用來存儲每個寶石的價值// prefix 用來存儲前綴和, 初始化為 0for (int i = 0; i < n; i++) cin >> a[i];sort(a.begin(), a.end());// 排序寶石的價值for (int i = 1; i <= n; i++) prefix[i] = prefix[i - 1] + a[i - 1];// 計算前綴和, 用于快速計算任意區間寶石的總價值ll ans = 0;int pos = 0;// ans 最大化寶石價值// pos 表示當前考慮的寶石區間的起始位置while (k >= 0) {ans = max(ans, prefix[n - k] - prefix[pos]);// 從剩下的寶石中選擇價值最大的 n-k 個寶石pos += 2; // 跳過兩個寶石, 因為每次處理我們都是取一對寶石k--;}cout << ans << "\n";}return 0;
}

解法二：

#include <bits/stdc++.h>/*
前綴和。
求出前綴和后，枚舉操作一的次數，即可獲得當前的答案，取 max 即可。
時間復雜度 O(n)
*/// 排序后, 留下開的寶石一定是連續的一段
// 可以發現, 這連續的一段一共只有 k + 1 種
// 枚舉刪除最大的刪除了多少個, 則立刻知道留下來的寶石是哪些
// 不能直接求和
// 前綴和可以解決using LL = long long;void solve(const int &Case) {int n, k;std::cin >> n >> k;std::vector<int> a(n);for (auto &x: a)std::cin >> x;std::sort(a.begin(), a.end());std::vector<LL> pre(n + 1); //注意long long for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] + a[i - 1]; //求前綴和LL ans = 0;for (int i = 0; i <= k; i++) { // 枚舉刪除最小的操作用了幾次// 設 i = 0, 可以發現留下來的是 1 2 3 ... n - k// 設 i = k, 可以發現留下來的是 2 * k ... n - 1ans = std::max(ans, pre[n - (k - i)] - pre[2 * i]);}std::cout << ans << '\n';
}//2 ^ 10 約等于 1000
//2 ^ 30 約等于 10^10
//計算機一秒跑 2 * 10^8int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T = 1;std::cin >> T;for (int i = 1; i <= T; i++)solve(i);return 0;
}

今天就先到這了！！！