題目描述

現有一棵由?n?個節點組成的無向樹，節點編號從?0?到?n - 1?，共有?n - 1?條邊。

給你一個二維整數數組?edges?，長度為?n - 1?，其中?edges[i] = [ai, bi]?表示樹中節點?ai?和?bi?之間存在一條邊。另給你一個整數數組?restricted?表示?受限?節點。

在不訪問受限節點的前提下，返回你可以從節點?0?到達的?最多?節點數目。

注意，節點?0?不?會標記為受限節點。

示例 1：

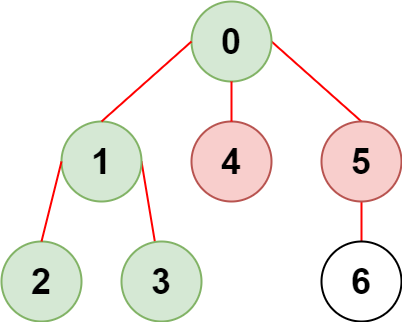
輸入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
輸出：4
解釋：上圖所示正是這棵樹。
在不訪問受限節點的前提下，只有節點 [0,1,2,3] 可以從節點 0 到達。

示例 2：

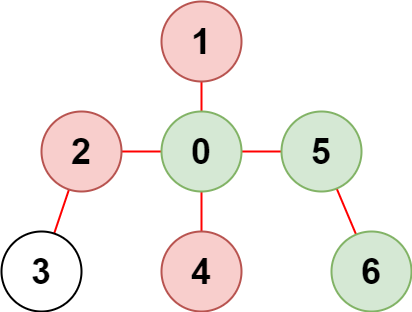
輸入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
輸出：3
解釋：上圖所示正是這棵樹。
在不訪問受限節點的前提下，只有節點 [0,5,6] 可以從節點 0 到達。

解題思路

本題并不難，解題主要是抓住題意，因為受限節點不可以訪問，所以我們可以直接將受限節點涉及到的邊直接排除在外，而后在驗證節點是否受限時，如果一個個查顯然時間復雜度過高，這時我們可以使用Set，減少查詢的時間復雜度。而后進行一次dfs就可以了，而后我們還需要知道，因為這是一棵樹，所以節點不會重復訪問，所以我們直接++即可。

代碼如下

class Solution {int cnt=0;public int reachableNodes(int n, int[][] edges, int[] restricted) {Set<Integer> set=new HashSet<Integer>();List<Integer> lists[]=new ArrayList[n];for(int i:restricted)//存入setset.add(i);for(int i=0;i<n;i++)lists[i]=new ArrayList<>();for(int i=0;i<n-1;i++){int x=edges[i][0];int y=edges[i][1];if(set.contains(x)||set.contains(y))//不進行邊加入continue;lists[x].add(y);lists[y].add(x);}boolean flag[]=new boolean[n];flag[0]=true;dfs(0,lists,flag);return cnt;}public void dfs(int p,List<Integer> lists[],boolean flag[]){cnt++;//不會重復直接++List<Integer> list=lists[p];for(int i=0;i<list.size();i++){int l=list.get(i);if(!flag[l]){flag[l]=true;dfs(l,lists,flag);flag[l]=false;}}}
}