Top-k問題
- 方法一:堆排序(升序)(時間復雜度O(N*logN))
- 向上調整建堆(時間復雜度:O(N * logN) )
- 向下調整建堆(時間復雜度:O(N) )
- 堆排序代碼
- 方法二:直接建堆法(時間復雜度:O(N+k×logN) ≈ O(N))
- 方法三:建一個k個數的小堆(時間復雜度O(k+(N-k)×logk)≈O(N))
方法一:堆排序(升序)(時間復雜度O(N*logN))
升序堆排序的一般思路就是將給定的一組數據放在堆得數據結構當中去,然后進行不斷被的取堆頂元素放在數組當中,不斷地pop(刪除)。但是這種方法太麻煩了,自己還要手寫一個堆的數據結構以及一些接口函數,還要創建數組等,顯然不是最優解。
接上文的寫的兩種調整方式,向上調整和向下調整。 詳細見
思路:
①可以用向上調整或者向下對原數組進行調整,也就是建一個大堆(排升序大堆后面講為啥)
②接下來利用堆刪除的原理,將堆頂的數據和數組最后一個交換(也就是將堆頂和堆尾的數據進行交換),然后就相當于最大的數放在了最后一個位置,所以最后一個位置的數據確定了,接下來對剩下的數據進行向下調整,再重復以上操作。
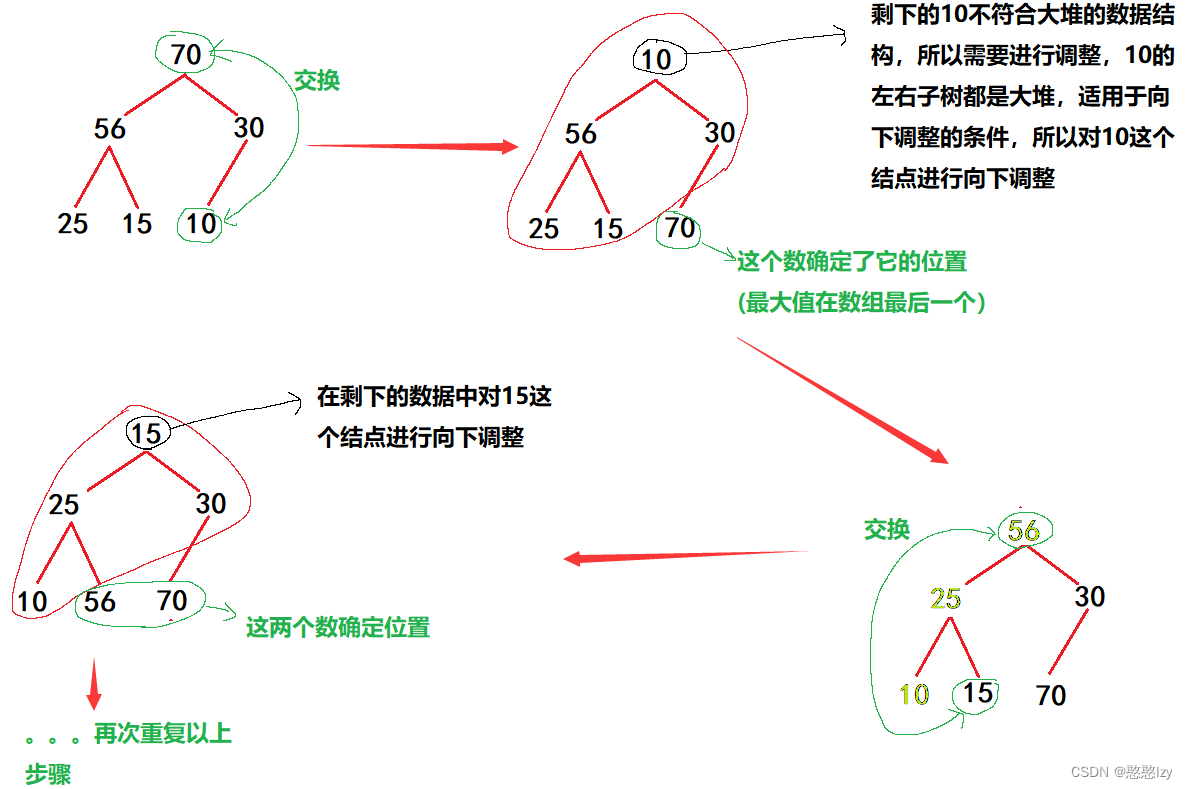
ps:排升序建大堆而不是小堆的原因,反證思路來看,若建小堆的話,最小的數據在第一個,第一個數據確定了,但是剩下的數據很暖再重新調整成為一個新的小堆的數據結構,所以排升序建小堆很難是實現
向上調整和向下調整都可以完成建堆的操作,但是他們的時間復雜度有所不同,接下來講一下他們的取舍。
向上調整建堆(時間復雜度:O(N * logN) )
for (int i = 1; i < n; i++){AdjustUp(a, i);}
因為堆是完全二叉樹,而滿二叉樹也是完全二叉樹,此處為了簡化使用滿二叉樹來證明(時間復雜度本來看的就是近似值,多幾個節點不影響最終結果):
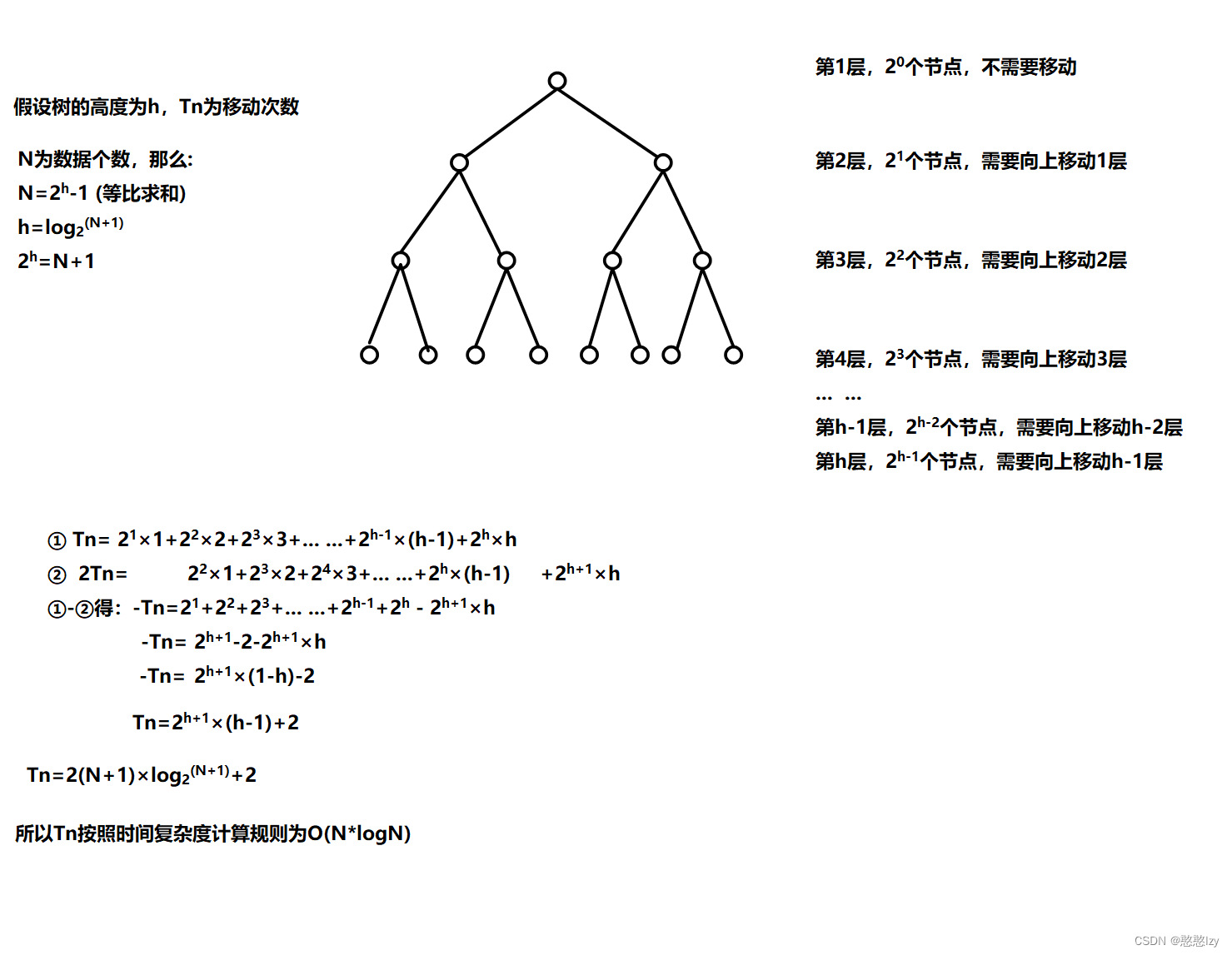
向下調整建堆(時間復雜度:O(N) )
for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);//a是堆的數組,n是防止數組越界的數組數據個數,i是開始向下調整的位置}
向下調整建堆得思路:從第一個非葉子結點開始從數組得后面向前面一個一個進行調整

復雜度證明:
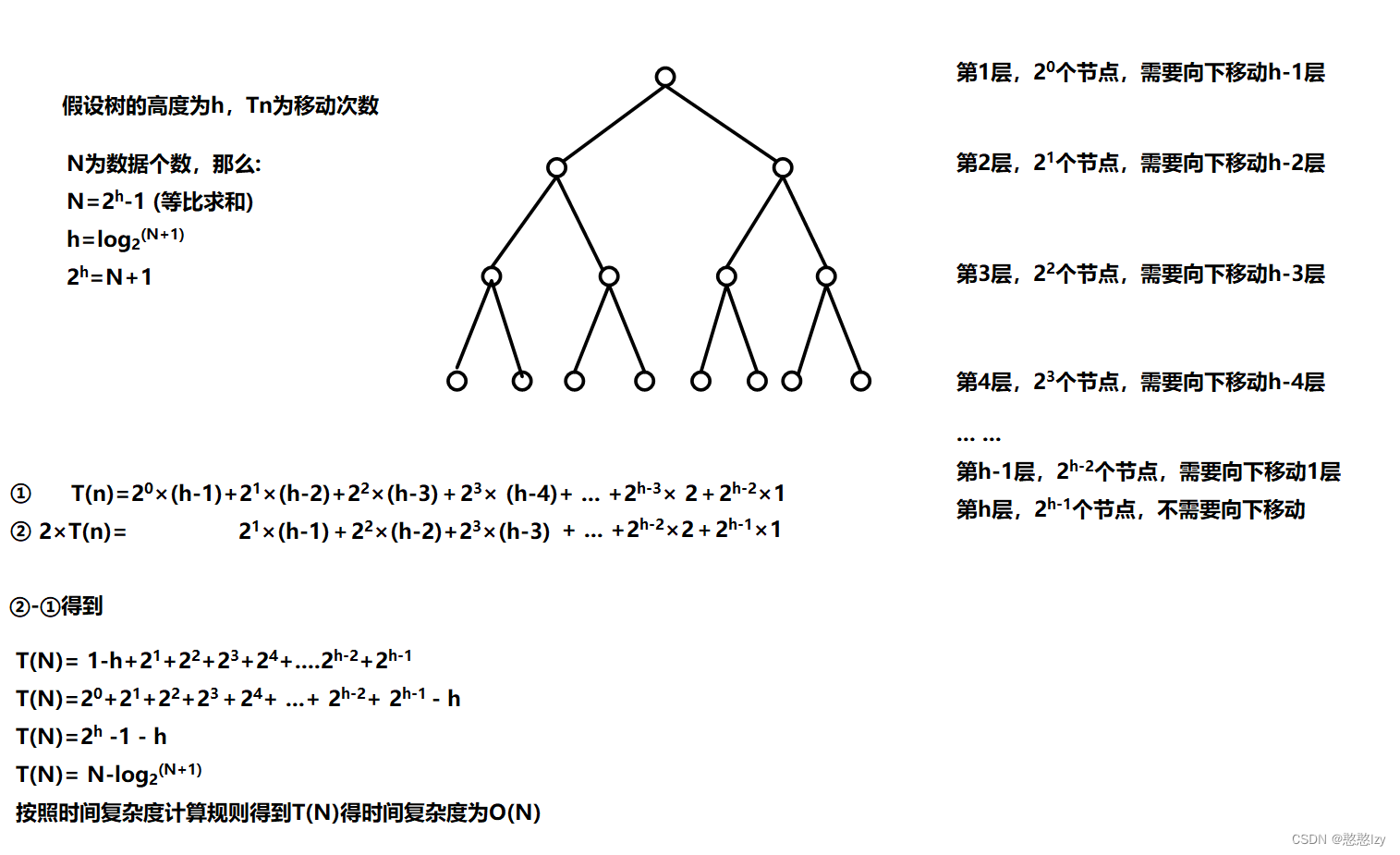
看到這里很容易發現向下調整方法建堆得時間復雜度更加合適
堆排序代碼
// 對數組進行堆排序
void HeapSort(int* a, int n)
{//思路:向上調整方法建堆建堆//>這里排升序要建大堆,因為建小堆的話,接下來排升序第一個數據好處理,//但是剩下的數據重新排成堆的話關系全都亂了//所以這時候建大堆,和刪除的思路一樣,首先交換堆頂和堆尾,這時候最大的數據放到了最后一個位置//然后將前面n-1個數據看成新的堆進行向下調整,然后再找次大的數放在倒數第二的位置//建堆有兩種方式 向上調整建堆和向下調整建堆,時間復雜度分別為O(N*logN)和O(N)//向上調整建堆 建堆時間復雜度 O(N*logN)/*for (int i = 1; i < n; i++){AdjustUp(a, i);}*///向下調整建堆 時間復雜度為O(N)//向下調整的條件是調整節點的左右子樹都為大堆或者小堆//所以從下邊開始進行向下調整(大堆),這時候大的數會慢慢上浮,最先調整的位置不能是葉子節點,那樣會重復很多操作//應該從最后一個父親節點開始進行向下調整 最后一個父親節點的下標為 (n-1)/2,然后按數組下標的順序遞減進行調整for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);//a是堆的數組,n是防止數組越界的數組數據個數,i是開始向下調整的位置}while (--n) //排序的時間復雜度為O(N*logN){//此處為--n的原因:一共有n個數據,循環一次確定一個數據的位置,循環n-1次之后就可以確定n-1個數據的位置,// 前面已經確定了n-1個位置,最后一個數據的位置也已經確定,所以當n=0的時候的那一次循環可以不需要進行就可以// //此時n已經自減1,所以此時n就為堆尾數據,且n為下一個新堆的數據個數,所以后面向下調整直接傳參nSwap(&a[0], &a[n]);//交換堆頂和堆尾的數據AdjustDown(a, n, 0);//n為新堆的數據個數}//總結:堆排序的時間復雜度為O(N*logN),因為堆排序有兩個步驟①建堆②排序//建堆向上調整建堆的時間復雜度為O(N*logN),向下調整建堆的時間復雜度為O(N),相對較快,//但是排序的時間復雜度都為O(N*logN),所以決定了堆排序的時間復雜度為O(N*logN)。
}
方法二:直接建堆法(時間復雜度:O(N+k×logN) ≈ O(N))
思路:有了堆排序中的向下調整建堆法,可以將這N個數建一個小堆,然后取堆頂元素打印,然后Pop(刪除)k次這樣稍微簡單些,但是當數據個數N太大得時候,對內存得要求很大,會占用很多內存,因為這種方法中,需要在堆區中創建一個N個數據的動態1數組,然后將數據放在數組當中去,因為如果在N很大的情況下,有可能你的設備內存并沒有那么大。所以這是這種方法的缺點。
一般數據都是放在磁盤或者文件中,所以我接口函數可以傳文件流
//創建隨機n個數據
void CreatData(int n)
{int k = 10;srand((unsigned int)time(NULL));//調用rand()的返回值形成隨機數必須調用srand函數//srand函數的形參為unsigned int類型的,且形參為不斷變化的數才可以生成為隨機數//所以形參傳參為時間戳函數time,time函數的形參得傳NULLconst char* file = "data.txt";FILE* pf = fopen(file, "w");if (pf == NULL){perror("fopen fail\n");return;}else{printf("打開成功\n");}for (int i = 0; i < n; i++){fprintf(pf, "%d\n", rand() % 10000);}fclose(pf);//關閉文件pf = NULL;
}//打印n個數據中最大的k個數據
void PrintTop1(const char* file, int k, int n)//n是數據個數
{FILE* pf = fopen(file, "r");if (pf == NULL){perror("PrintTop fopen fail");return;}//1.把n個數建大堆int* top = (int*)malloc(sizeof(int) * n);//創建一個動態數組存放堆的數據if (top == NULL){perror("top malloc fail\n");return;}//讀取n個數放在堆當中去for (int i = 0; i < n; i++){fscanf(pf, "%d", &top[i]);}//向下調整建大堆for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(top, n, i);}//打印 k次堆頂元素for (int i = 0; i < k; i++){printf("%d ", top[0]);//打印堆頂元素Swap(&top[0], &top[n - i]);AdjustDown(top, n - i - 1, 0);//這里交換后的那個數據不能算入內}
}
//測試CreatData(10000000);//創建數據
PrintTop1("data.txt", 10,10000000);//這里測試時候可以直接只改PrintTop1中n的大小,因為前面CreatData創建數據會花費很多時間,導致第二個函數并不能直接運行//CreatData(10000000);//創建數據
//PrintTop1("data.txt", 10, 100000000);//CreatData(10000000);//創建數據
//PrintTop1("data.txt", 10, 1000000000);代碼先放在這里,接下來我來驗證:
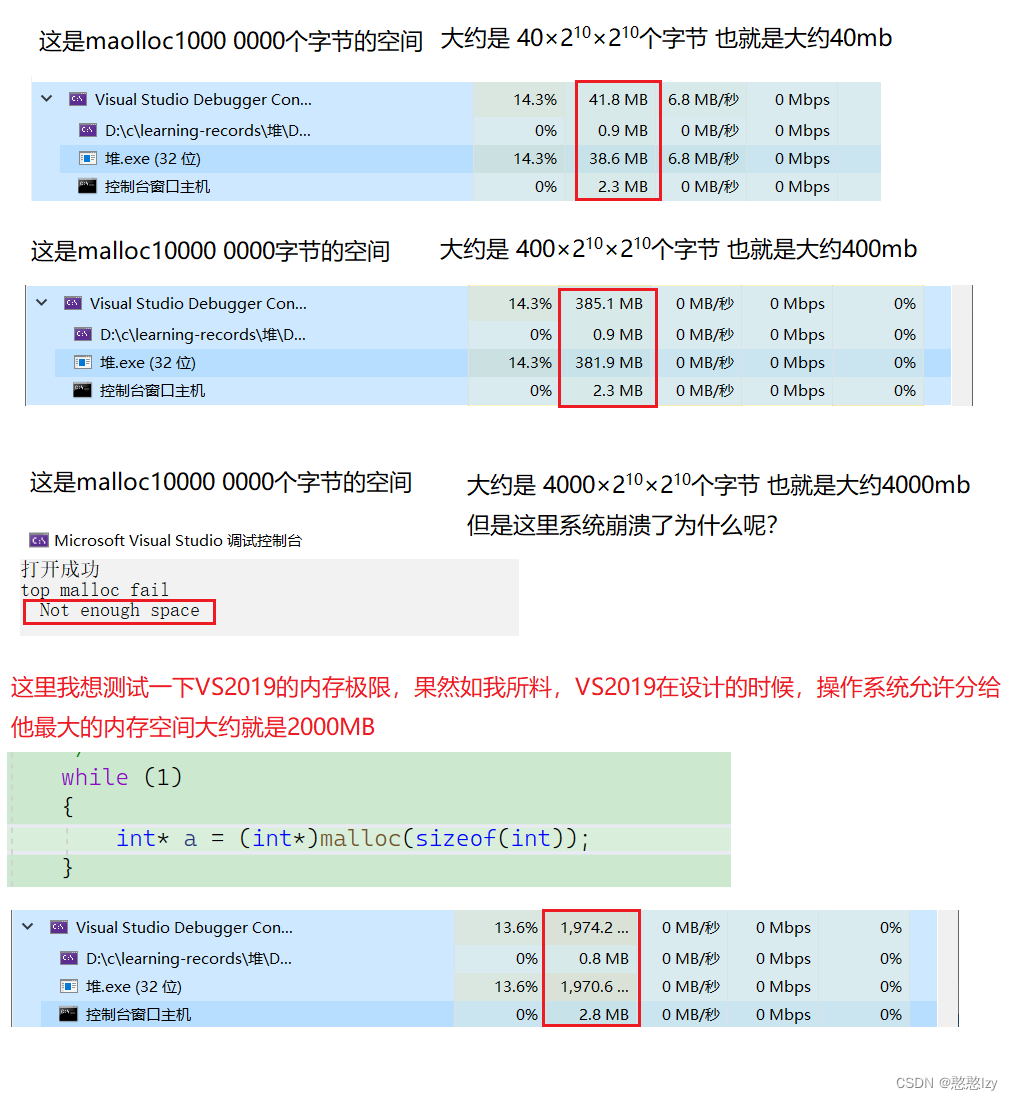
所以這種方法當數據N很大的時候并不可取
方法三:建一個k個數的小堆(時間復雜度O(k+(N-k)×logk)≈O(N))
思路:取前k個數建立一個k個數的小堆,然后遍歷剩下的所有數據,并和堆頂進行比較,只要比堆頂大就和堆頂交換,然后進行調整,然后進行循環,遍歷結束之后也就證明這k個數為所要求的k個數。例如:
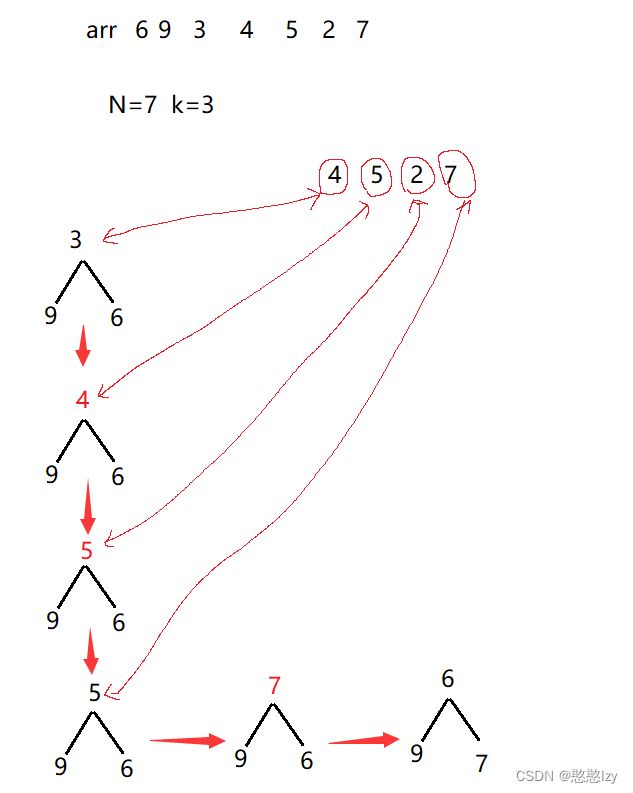
代碼:
//小堆的向下調整 和大堆的向下調整一樣
void AdjustDownSmall(HPDateType* a, int n, int parent)//向下調整(小堆) 時間復雜度O(logN)
//向下調整的條件是調整節點的左右子樹都為大堆或者小堆
//思路為從下標為parent位置開始向下的孩子節點不斷比較進行調整,直到最后一個數據,
//所以需要傳參堆的有效數據個數n
{int leftchild = parent * 2 + 1;while (leftchild < n)//{int rightchild = parent * 2 + 2;if (rightchild < n && a[leftchild] > a[rightchild]){//判斷一下該父親節點是否有右孩子,防止數組越界//默認左孩子小于右孩子//若右孩子小于左孩子則交換下標Swap(&leftchild, &rightchild);}if (a[parent] > a[leftchild]){Swap(&a[parent], &a[leftchild]);//若不符合堆的要求則交換parent = leftchild;//將原父親數據對應下標也賦值過來leftchild = parent * 2 + 1;//新的孩子的下標}else//若符合堆的要求就退出循環{break;}}
}//Top-k 問題 取前k個較大的數
void PrintTop(const char* file, int k)//把文件傳進來和需要找的前k個數
{FILE* pf = fopen(file, "r");if (pf == NULL){perror("PrintTop fopen fail");return ;}//1.把前k個數建小堆int* top = (int*)malloc(sizeof(int) * k);//創建一個動態數組存放堆的數據if (top == NULL){perror("top malloc fail\n");return;}//從文件中讀取k個數據放在數組中for (int i = 0; i < k; i++){fscanf(pf, "%d", &top[i]);}for (int i = (k - 1) / 2; i >= 0; i--){AdjustDownSmall(top, k, i);}//2.遍歷剩下的n-k個數并與堆頂作比較,若比堆頂大則交換然后再進行向下調整int val = 0;int ret = fscanf(pf, "%d", &val);while (ret != EOF){if (val > top[0]){Swap(&val, &top[0]);AdjustDownSmall(top, k, 0);}ret = fscanf(pf, "%d", &val);}//打印數組for (int i = 0; i < k; i++){printf("%d\n", *(top+i));//printf("%d\n", top[i]);//會報錯C6385//像數組一樣在連續內存空間存儲的多個數據才使用下標法//這種應該是編譯器問題 具體不清楚}free(top);top = NULL;fclose(pf);pf = NULL;
}
分析:對比時間復雜度方法二和方法三的時間復雜度都差不多,方法三在N為很大的情況下,所用內存空間是取決于k的,因為k一般是一個很小的數一般不會很大,導致內存崩潰。
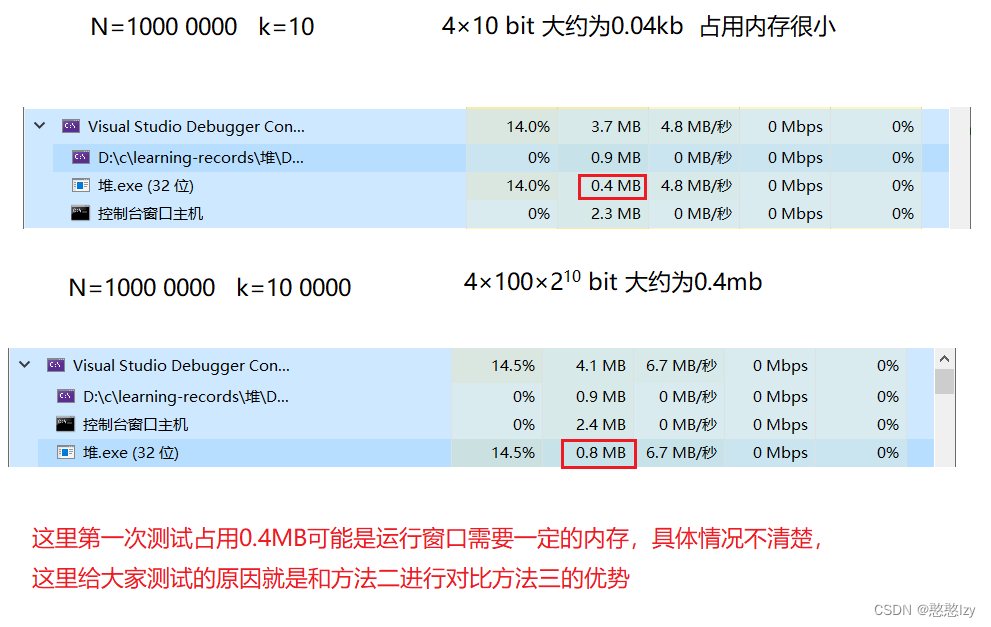
方法二 方法三自己實測其實時間上,對于1000 0000個數據的時候運行的時候都會大約等待個5 6秒,所以他們的時間復雜度大差不差,優勢在于空間的使用。







)
)




)





