目錄

一、什么是遞歸

1.1.遞歸的思想

1.2.遞歸的限制條件

二、舉例體會

2.1.求n的階乘?

2.2.順序打印整數的每一位

2.3.斐波那契數列

三、遞歸與迭代

---

一、什么是遞歸

在學習C語言的過程中，我們經常會跟遞歸打交道，什么是遞歸呢？它其實是一種解決問題的方法，遞歸遞歸，顧名思義，遞推和回歸。在C語言中，函數自己調用自己就是遞歸，我們可以把它想成生活中的俄羅斯套娃。

下面請看最簡單的遞歸代碼：

#include <stdio.h>
int main()
{printf("hehe\n");main();//main函數中?調?了main函數return 0;
}

在上面的代碼中，我們看到了main函數里再次調用了main函數，我們可以想象，這個程序會一直調用下去，直到，內存不夠導致棧溢出（Stack overflow）。

1.1.遞歸的思想

遞歸的思想用一個詞來講就是“大事化小”。

其中遞代表遞推，歸代表回歸。

1.2.遞歸的限制條件

剛剛我們看到，一直調用main函數的話，會造成死遞歸，因此，我們在使用遞歸時需要注意一些必要條件。

1.遞歸存在限制條件，當超過這個限制條件時遞歸就應該停止

2.每次遞歸應該越來越接近這個限制條件。?

接下來我們舉幾個例子來讓大家體會一下這兩個必要條件。

二、舉例體會

2.1.求n的階乘?

?個正整數的階乘（factorial）是所有?于及等于該數的正整數的積，并且0的階乘為1。

?

自然數n的階乘寫作 n! 。

經分析可知n! = n * (n-1) * (n-2)... * 3 * 2 * 1,而（n-1)! = (n-1) * (n-2) *...* 3 * 2 * 1。

所以n! = n * (n-1)!。

我們要求n的階乘，只需要求n和n-1的階乘的乘積，問題也就變成了求n-1的階乘。經過一次遞歸，我們就從n變到n-1，那遞歸的次數足夠了，我們就可以到最后的1的階乘。那怎么得到n的階乘呢，我們剛剛一步一步得到1的階乘，那我們再一步一步乘回去，最終得到n的階乘。

上述思路就是所謂的遞歸，也就是把一個較大的問題轉換為與原問題相似的小問題。

當n = 0時，n! = 1。我們可以得到遞推公式：

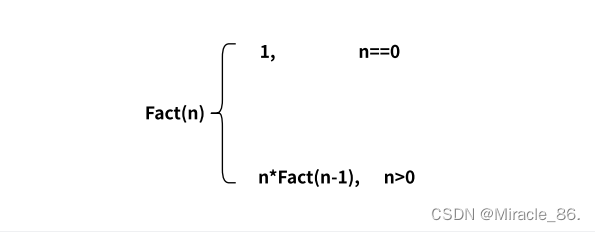
代碼如下：

函數部分

int Fact(int n)
{if(n==0)return 1;elsereturn n*Fact(n-1);
}

總體

#include <stdio.h>
int Fact(int n)
{if(n==0)return 1;elsereturn n*Fact(n-1);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fact(n);printf("%d\n", ret);return 0;
}

測試結果

2.2.順序打印整數的每一位

輸入一個整數n，順序打印其每一位。

input : 1234

output : 1 2 3 4

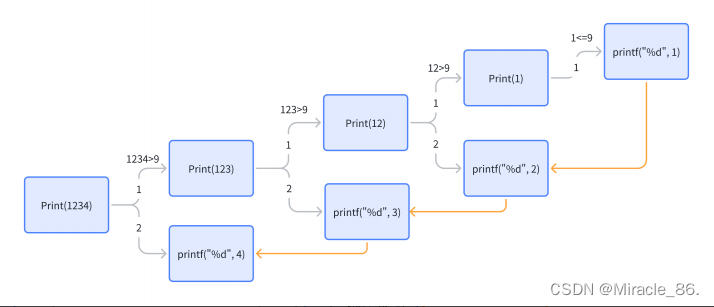
分析可知，1234/10 = 123，而1234%10 = 4。那我們可以巧妙的利用上述特性，得到1234的每一位。但是出現一個問題，我們獲得的數字的順序是倒著的，這該怎么辦呢。我們可以仔細品味一下遞歸，遞推和回歸，先遞推再回歸。

我們就可以先進行/10的操作，再打印%10的余數，如下：

void Print(int n)
{if(n>9){Print(n/10);}printf("%d ", n%10);
}

畫圖推演一下：

代碼如下：

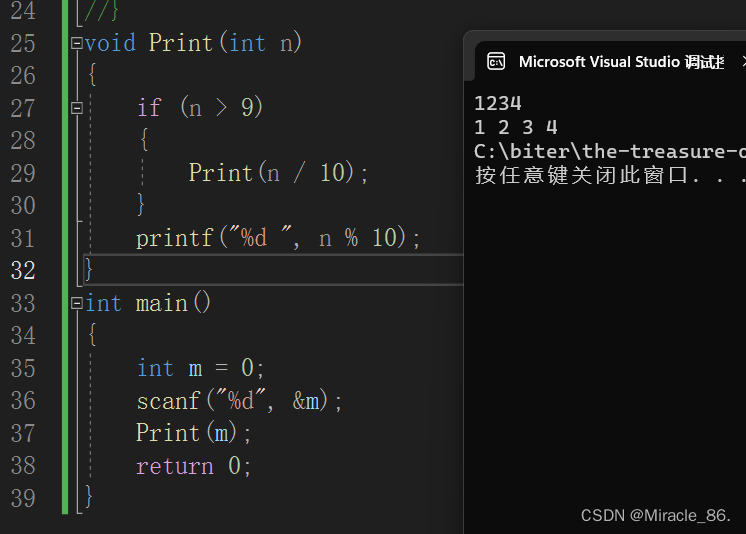
#include<stdio.h>
void Print(int n)
{if (n > 9){Print(n / 10);}printf("%d ", n % 10);
}
int main()
{int m = 0;scanf("%d", &m);Print(m);return 0;
}

運行結果：

2.3.斐波那契數列

斐波那契數列（Fibonacci sequence），又稱黃金分割數列，因數學家萊昂納多·斐波那契（Leonardo Fibonacci）以兔子繁殖為例子而引入，故又稱“兔子數列”，其數值為：1、1、2、3、5、8、13、21、34……?

其遞推公式為

用遞推寫出代碼很簡單：

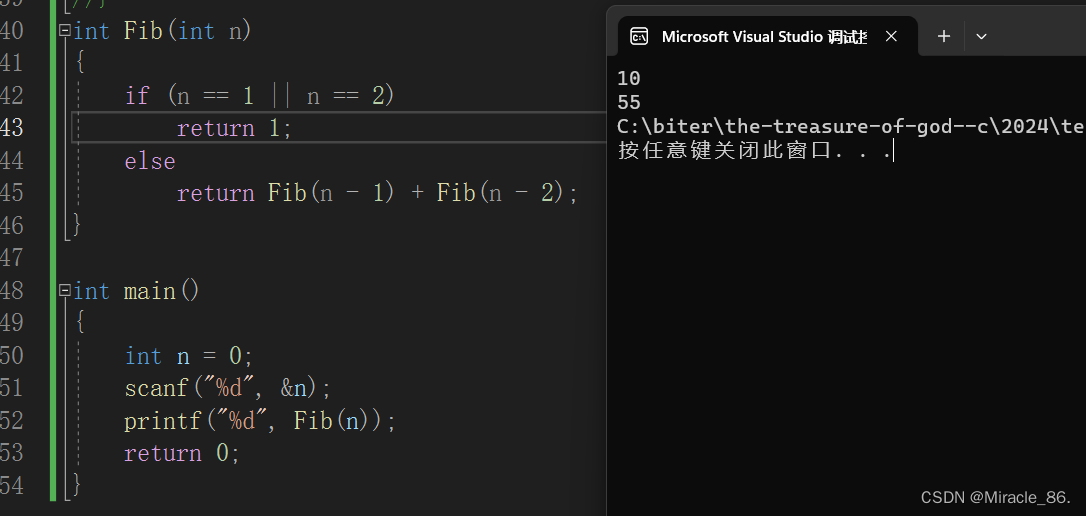
#include<stdio.h>int Fib(int n) 
{if (n == 1 || n == 2)return 1;else return Fib(n - 1) + Fib(n - 2);
}int main()
{int n = 0;scanf("%d", &n);printf("%d", Fib(n));return 0;
}

運行結果：

那如果讓你不用遞歸的方法，你會怎么做呢？?

我們可以創建三個變量，就像兩個數互相交換那樣，將a賦值1，b賦值1，c為a與b的和。

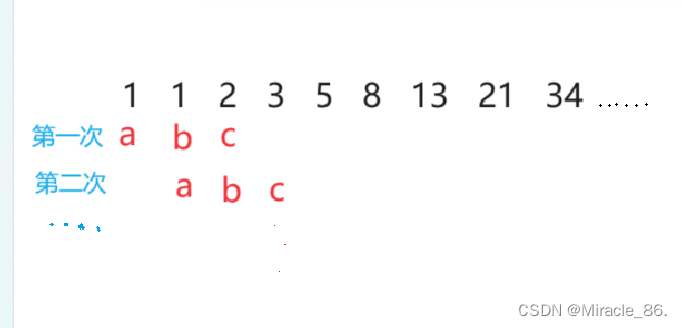
n大于二之后才開始循環，所以我們可以這么寫：

int Fib(int n) 
{int a = 1, b = 1,c = 0;while (n>2){c = a + b;a = b;b = c;n--;}return b;
}

?一個接著一個交換值，直到n等于2，退出循環，此時c的值賦給了b,而我們在n小于等于2的時候，求不出來c，而b的值正好是1，所以我們返回b的值。

三、遞歸與迭代

上面我們說了什么是遞歸，這又來個迭代，什么叫迭代呢？說白了通常就是循環。

比如剛才計算階乘，我就不想用遞歸，那我就循環n次，也可以解決問題，并且該方法效率比遞歸高。

我們遇到的許多問題用遞歸解釋的原因是因為，它比非遞歸好想好解釋，但這些問題往往迭代比遞歸的效率更高。

我們說當一個問題非常復雜，難以用迭代的方式來解決時2，這時候遞歸實現的簡潔性便可以補償運行時的開銷。

就像剛剛的例三，求斐波那契數列，使用迭代的方法就更加有效率。

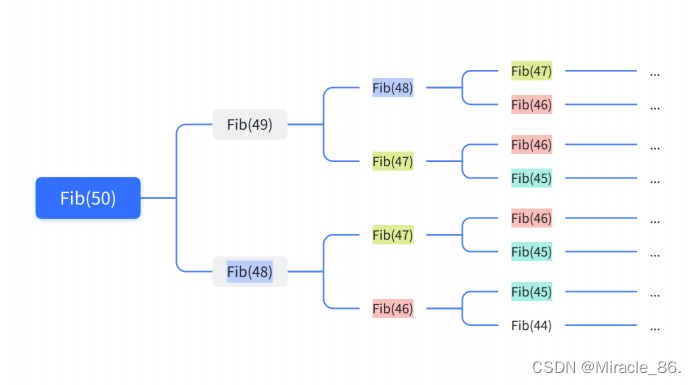
如圖所示，遞歸層次越深，冗余計算越多，我們可以簡單測試一下

#include <stdio.h>
int count = 0;
int Fib(int n)
{if(n == 3)count++;//統計第3個斐波那契數被計算的次數if(n<=2)return 1;elsereturn Fib(n-1)+Fib(n-2);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret); printf("\ncount = %d\n", count);return 0;
}

?來看結果

這才是40,可想而知50會是多大的天文數字。

而迭代的方式，我們只需要前后一步一步相加即可。

---

最后總結一下，遞歸是一個很好的解決問題方式，在編程學習中，我們會經常用到它，但是它也不是萬能的，還是需要我們多動腦思考。

我相信，我們總會找到解決辦法的。