TGD 是我們定義的一種新的“變化率表征”，對連續函數而言是一種新的“廣義導數”，對離散序列而言是一種新的差分。TGD 是一個名字，一個代號。在基于 TGD 的圖像邊緣檢測以及視頻邊緣檢測中，我們發現輸入序列卷積 TGD 算子得到的響應結果，帶來了邊緣檢測的優異結果。為此，我們猜測，信號的 TGD 值能夠被視作一種特征，即「 TGD 特征 」，并且做很多其他事，服務很多 CV 計算機視覺任務。至于能做什么，不知道，既然不知道，那就交給神經網絡作為特征好了。為此則有了本章節“當神經網絡遇到 TGD 特征（When TGD features meet Neural Network）”。感興趣的朋友歡迎閱讀詳見前面的章節：

理論部分：

TGD 第一篇：初心——我想要為“階梯函數”求導。

TGD 第二篇：破局——去除導數計算中的無窮小極限。

TGD 第三篇：革新——卷積計算導數的高效之路。

TGD 第四篇：初瞰——抗噪有效的定性計算。

TGD 第五篇：飛升——給多元函數的導數計算加上全景雷達。

TGD 第六篇：落地——離散序列的 TGD 計算。

傳統計算機視覺應用部分：

TGD 第七篇：一維應用——信號去噪和插值。

TGD 第八篇：二維應用——圖像邊緣檢測。

TGD 第九篇：三維應用——視頻邊緣檢測。

一、實驗背景

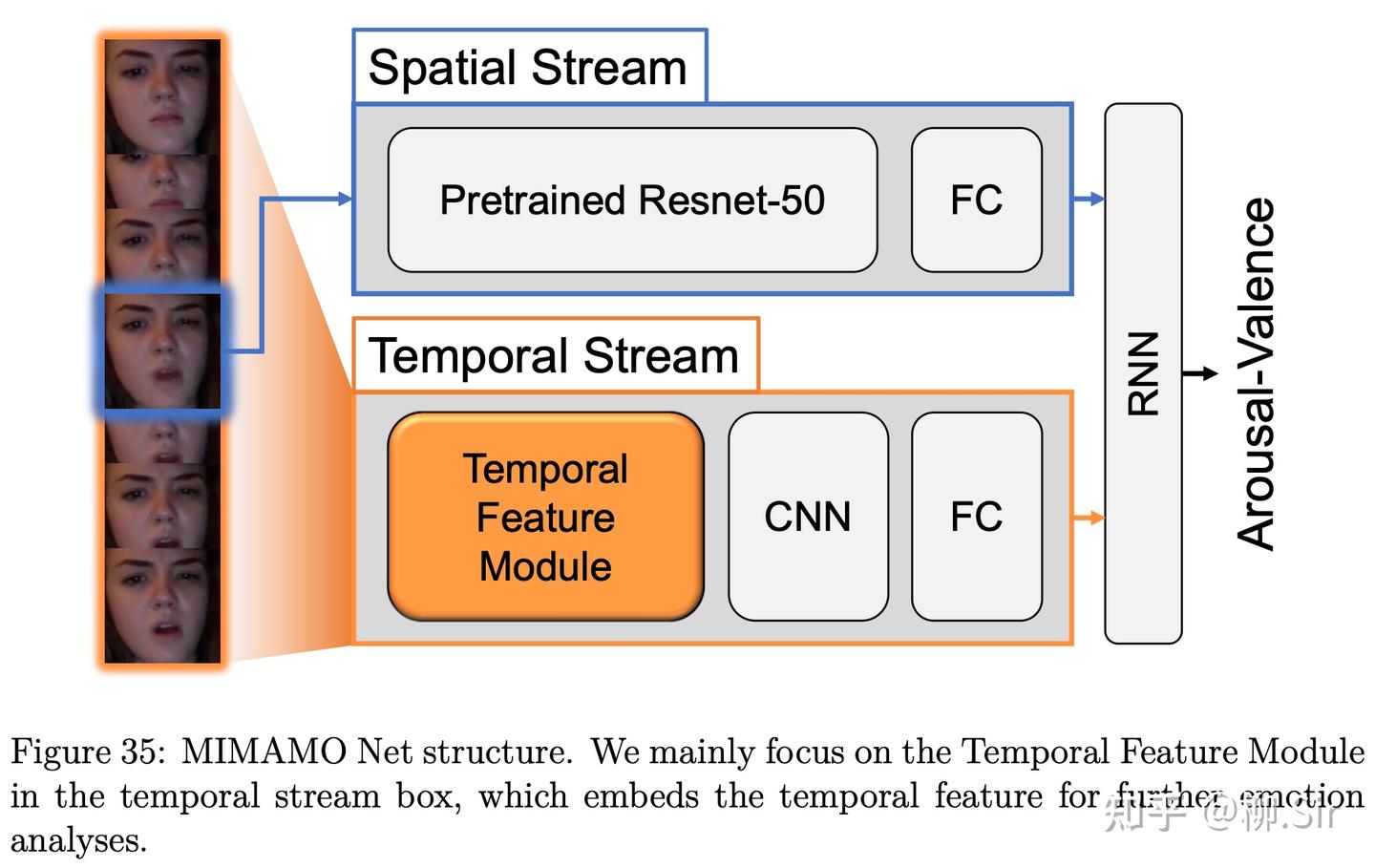
2021 年春，我選修了孫延奎老師開設的《小波分析及其工程應用》，課程非常好，并且在課程上遇到了“官佳智”大佬，當時大作業要求用小波做想做的任何事。當時是 2021 年春夏之交，經過調研和論文搜索，官佬找到了 AAAI2020 剛剛入選的一篇文章 MIMAMO Net¹（Micro-Macro-Motion Net）。并找到了其 Github 鏈接，基于此開展實驗。該工作將連續視頻幀作為輸入，反正經過“吧啦吧啦吧啦”²得到了一組特征，來表征連續幀之間的時序特征，并將該時序特征引入深度神經網絡中，在“視頻人臉情感識別任務”中取得了 SOTA 的表現。MIMAMO 框架如下圖所示，模型輸入是連續幀圖像。在對每一幀的預測過程中，Spatial stream 由預訓練的 Resnet50 網絡提取該靜態幀的結構特征，Temporal stream 用相位差特征作為輸入，利用一個多層 CNN 進行編碼，最后多幀的空間特征（Spatial Feature）和時序特征（Temporal Feature）拼接后經過 RNN 編碼輸出 valence-arousal 的預測結果。他的大作業就是把 MIMAMO 中的傅立葉相位差特征變成小波系數做差得到的特征。

大作業答辯的時候，聽了官佬的答辯，我說相鄰兩幀直接做差不好，我的研究就是離散序列如何計算變化率！于是就和他交流了 TGD 的思想（當初的取名還叫做窗導數，Window Derivative，所以后面的一些圖中會看到「WD」）。為此，這個實驗是在官佬的大作業基礎上繼續做出來的，下面的實驗當時由官大佬主導完成。

首先讓我們分析一下“視頻人臉情感識別任務”和TGD的適配性，即根據輸入視頻中人物的面部動作、微表情等特征，判斷人物實時的情感狀態。而臉部在時間維度上的像素值的變化，恰好能夠表征人臉面部器官、肌肉等變化特征。在時間方向的一階TGD響應中，紅色為未來將出現運動的部分，藍色部分為過去消失運動的部分；在時間方向的二階TGD響應中，藍色為當前即將運動的部分，紅色為過去和未來運動的部分，顏色越鮮艷變化速度越快。之前的實驗應用已經看到TGD能夠表征時間上的像素變化，那么將其放入神經網絡，會帶來什么驚喜呢？

二、實驗設置

【TGD 算子】我們基于正交構造法，使用高斯權重分布函數構造三維一階和二階 TGD 算子，求導方向為時間軸方向。

【數據集】與 MIMAMO 論文保持一致，實驗使用數據集是 Aff-Wild³。該數據集包含了一共 $298$ 段從 Youtube 收集的、表達了人們情感變化的長視頻。這些視頻中一共有 $200$ 個不同的人物，包含了不同的種族、膚色、性別，總時長超過了 $30$ 小時。這些視頻的每一幀都由 $8$ 位不同的人員在 valence-arousal 連續空間（取值范圍 $[?1,1]$ ） 進行了標注，任意一幀圖像的 valence （情感是多么積極或消極、正向或負向) 和 arousal （情感的強度） 值共同表現了當前時刻人物的情感特征。

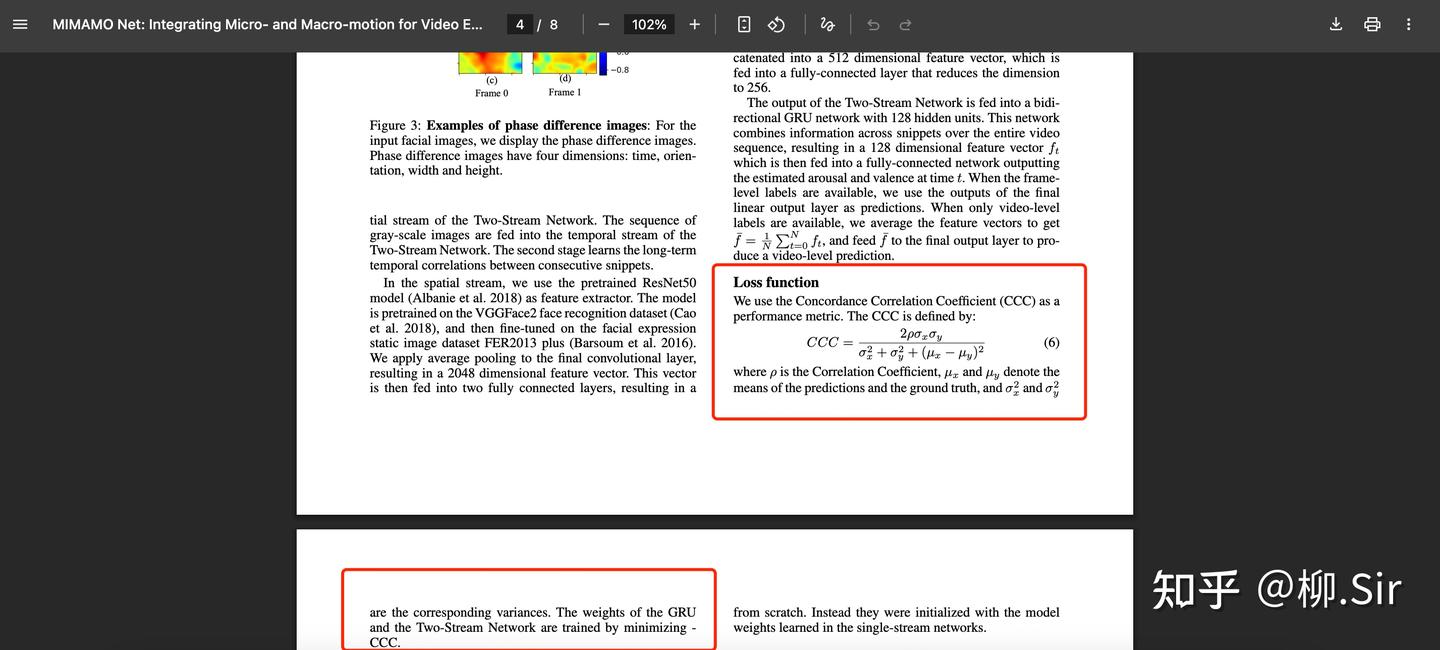
【評價指標和損失函數】與 MIMAMO 論文保持一致，實驗中評價指標為一致性相關系數 Concordance Correlation Coe?icient (CCC)，并且損失函數為最小化負一致性相關系數。

【對比設置】為了驗證「 TGD 特征 」在的性能，我們僅僅在上圖所示的 MIMAMO Net 的網絡架構替換輸入的時序特征（Temporal Feature），保持其他網絡結構不動，展開實驗。也是結合了剛上完的小波課程，我們嘗試直接在 RGB 域（即不對原始輸入幀進行變換）和小波域，利用三維 TGD 構建更為高效的面部時序特征。實驗共設置了七組時序特征作為對比：

• 第一組：FT 相位差特征，即 MIMAMO 論文初始配置
• 第二組：小波系數直接做差，Wavelet Transform Difference（Wavelet-Diff）: 利用 Haar 小波變換獲得每一幀的小波系數，使用連續幀之間的小波系數差作為時序特征。
• 第三組：小波系數+高斯平滑求導，Wavelet Transform & Gaussian Derivative (Wavelet-GD)：利用 Haar 小波變換獲得每一幀的小波系數，對幀內小波系數進行二維高斯平滑，且替換相鄰幀差為卷積一維高斯一階和二階導數卷積核作為時序特征（這組實驗的設置和圖像邊緣檢測中的對比設置一致，告訴大家高斯平滑在變化率表征中不好用）。
• 第四組：小波系數+ TGD，Wavelet Transform & TGD(Wavelet-TGD)：利用 Haar 小波變換，替換相鄰幀差為卷積時間方向一階和二階三維 TGD 算子作為時序特征。
• 第五組：連續幀直接做差，Frame Difference(Frame-Diff)：直接利用連續幀之間的差值直接作為時序特征。
• 第六組：連續幀+ 高斯平滑求導，Frame & Gaussian Derivative (Frame-GD)：對幀內進行高斯平滑，且替換相鄰幀差為卷積一維高斯一階和二階導數卷積核作為時序特征。
• 第七組：連續幀+ TGD，Frame & TGD (Frame-TGD)：替換相鄰幀差為卷積時間方向一階和二階三維 TGD 算子作為時序特征。

原始 MIMAMO 通過連續 $13$ 幀經兩個方向帶通濾波和降采樣獲得 $48$ 個相位差特征。針對第五至第七組實驗設置， $13$ 個連續幀經幀間直接做差得到 $12$ 個時序特征；對于高斯平滑求導，幀內使用 $7\times 7$ 的高斯平滑核 (高斯方差 $\delta =1$ )，時間方向使用長度為 $11$ 的高斯一階導算子和二階導算子(高斯方差 $\delta =1.7$ ))，可獲得 $3$ 個一階以及 $3$ 個二階導數特征，合計 $6$ 個時序特征；對于 TGD，三維 TGD 算子卷積核尺寸為 $7\times 7\times 11$ ，由于使用正交構造法，等效于幀內進行 $7\times 7$ 高斯積分平滑核進行平滑（高斯方差 $\delta =1$ ），時間方向高斯方差取 $\delta =1.7$ ，可獲取到 $3$ 個一階 TGD 以及 $3$ 個二階 TGD 特征，合計 6 個 TGD 時序特征。而在小波域中（第二至第四組實驗設置），水平和豎直方向的高低頻特征分別計算，所以得到 4 倍于第五至第七組實驗設置的特征數量。

從時空梯度特征的角度來看，對于一秒 $20$ 幀的視頻，兩幀直接做差的方法得到的單個特征僅使用了 0.05s 內的運動信息，計算得到的數值極易受噪聲影響。相較而言，TGD 算子對連續 $11$ 幀進行卷積計算，單個特征能使用 0.5s 內的信息，在時間維度上具有更大的跨度（ $10$ 倍于兩幀做差的算法），能夠一定程度上實現降噪。

為了和 MIMAMO 保持一致，時序特征被設置為與神經網絡訓練解耦合的步驟，即在訓練神經網絡前完成時序特征的計算和存儲。但是值得指出的是，TGD 計算其實是用三維卷積核卷積連續幀。為此，TGD 算子的數值其實可以作為三維卷積層的初始化卷積核參數，構造的卷積層能直接作為神經網絡的一部分在初始階段進行特征提取。每組實驗都運行了三次取平均值。

三、實驗結果和分析

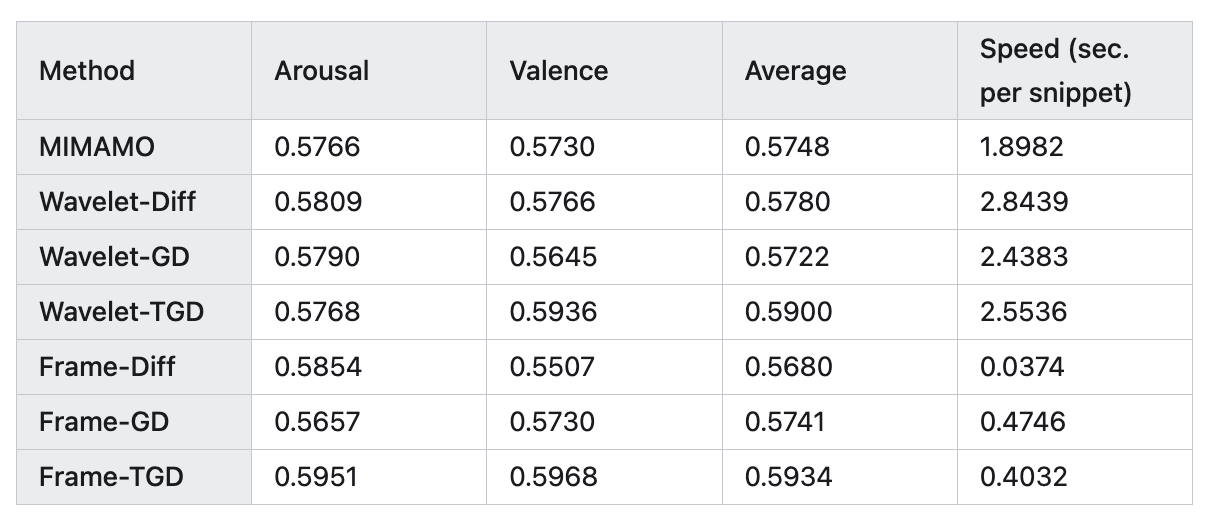
定量的實驗結果上表所示，TGD 最優！

實驗看起來小波系數直接做差，比 MIMAMO 論文中的傅立葉系數濾波后做差還要好，然后小波系數的 TGD 作為時序特征，性能還有提升。原始幀直接做差可能不如小波系數（Wavelet-Diff）和傅立葉系數做差（MIMAMO），更令我驚訝的是，直接原始幀的 TGD 作為時序特征，效果最好！并且TGD特征生成速度是傅立葉變換和小波變換的 $4.7$ 倍和 $6.2$ 倍。

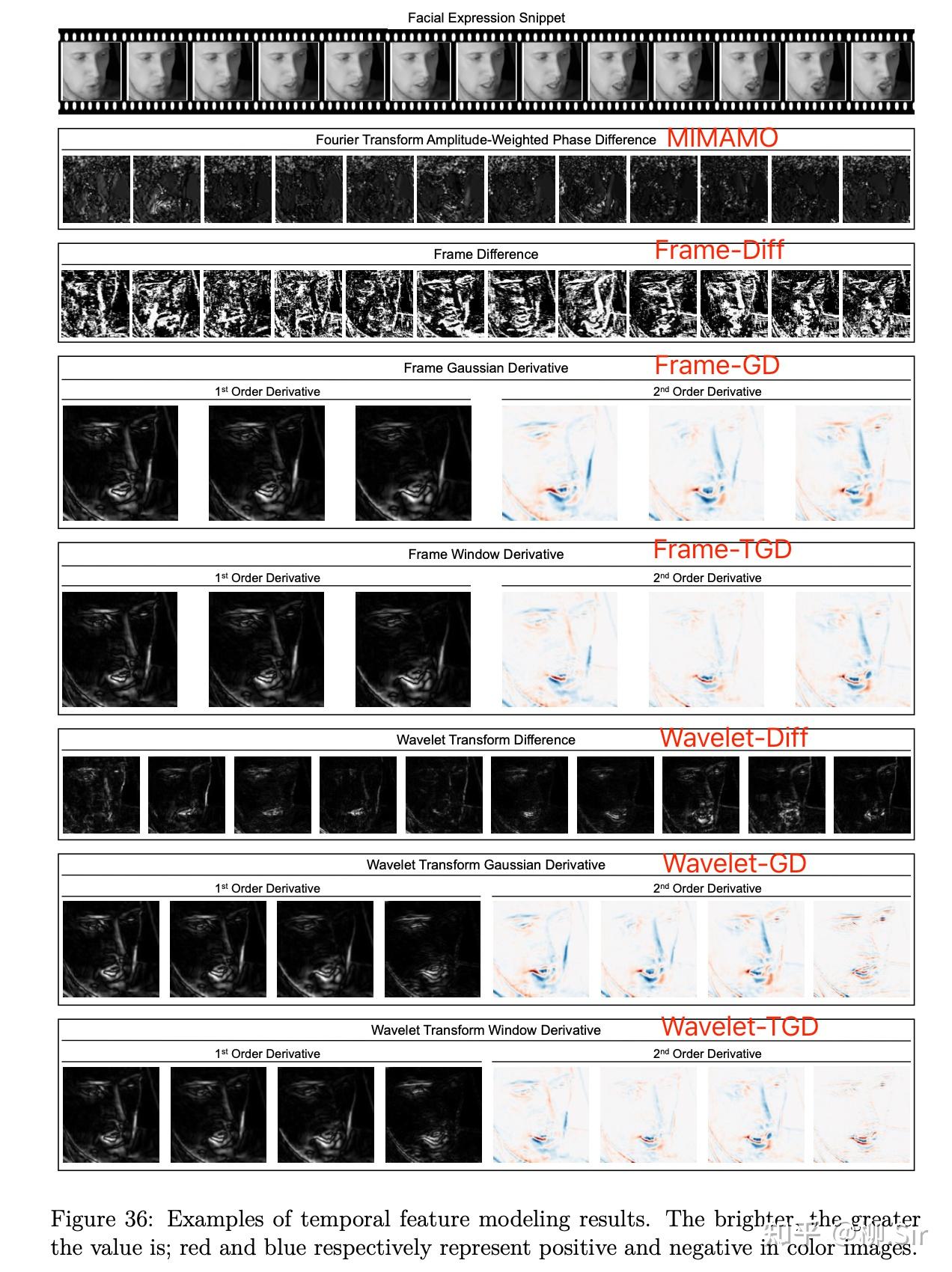
除了定量的比較，我們還可視化了不同輸入時序特征（圖中 Window Derivative 就是 TGD），首行為連續 $13$ 個輸入幀；第二行為 MIMAMO 的輸入時序特征，因為是傅立葉變換的相位，基本看不出來幾何屬性， 可解釋性較差 ；第三到第八行的可視化結果則展現了人的面部變化特征，更直觀，具有更強的可解釋性。第三行為連續兩幀直接做差，受到了極大的噪聲影響；第四到第八行看起來效果差不多，小波低頻系數和高斯平滑求導、TGD 都能實現一定的去噪，并且捕捉面部變化的部分。

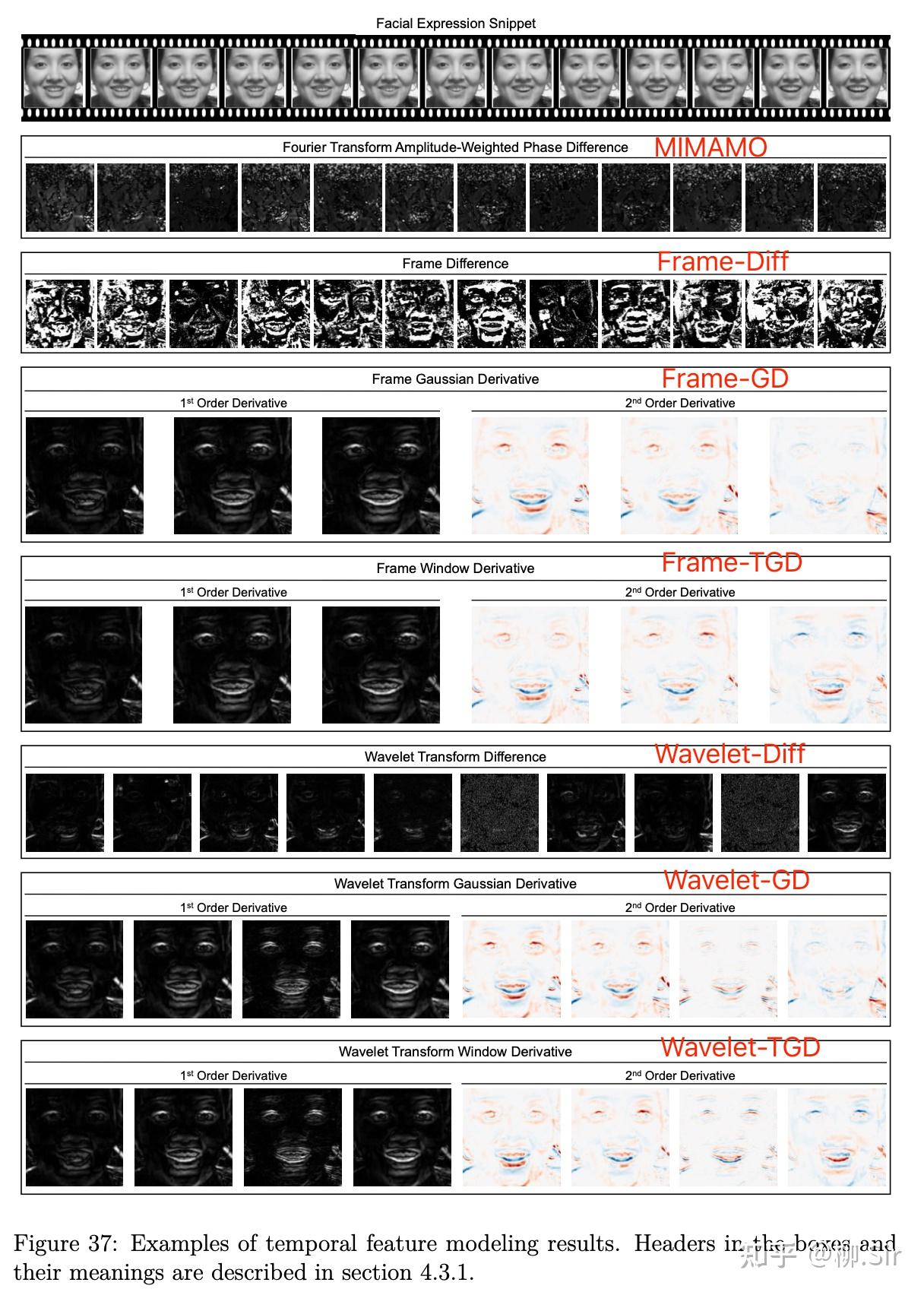
既然看不出什么差別，我就再往后看一層。下圖可視化了不同的時序特征經過神經網絡第一層卷積層后的激活圖（activation map）。MIMAMO 確實可解釋性太差，Frame-Diff 的結果依舊存在很多噪聲。無論是幀像素值還是其小波系數，高斯平滑求導以及 TGD 得到的激活圖中都可見清晰的人臉運動輪廓，然而兩者對比，TGD 得到的激活圖對運動區域的定位更“干凈”更精確，而高斯平滑求導由于定位漂移等缺點，生成的時序特征會一定程度上誤導神經網絡，從而會出現一些奇奇怪怪的“不干凈”的激活圖，我認為這些“不干凈”的激活圖是用來矯正彌補高斯平滑求導帶來的信息失真的。這也是為什么 Frame-GD 不如 Frame-TGD，Wavelet-GD 不如 Wavelet-TGD 的原因。

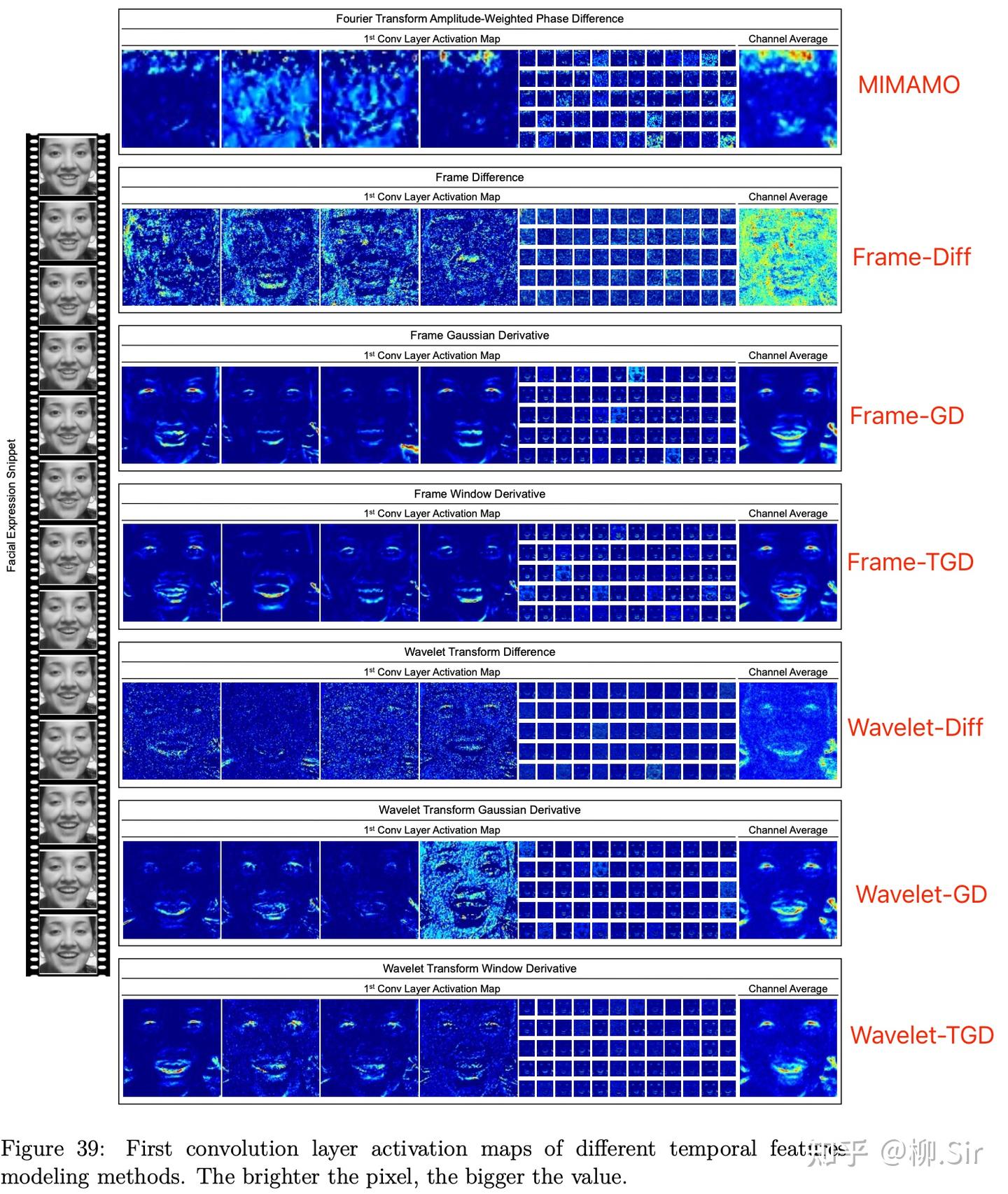
四、結語

本次實驗其實是 2021 年的故事，對比研究和分析在當時可能還微微有所貢獻，對于推動今天“視頻人臉情感識別任務”發展基本沒有什么貢獻。應用的每一個篇章我都會強調，做這些實驗的目的不是解決某個具體問題，不是刷榜和SOTA。

馬克思提出： 生產工具是衡量生產力發展水平的客觀標志，生產工具的改進和變革直接反映生產力水平，但需通過人的勞動實現。 TGD 就是一個新的生產工具，用來表征函數和信號變化率，TGD的提出將提升生產力水平，但還需要諸多研究者接續在下游任務中應用實現。我想做的，就是告訴大家TGD這個新的生產工具是有實際使用價值的，希望引起大家的共鳴，僅此而已。

誠然，在如今端到端大語言模型（LLM）的時代，幾乎沒有研究者再來關注一個一個微小的任務，在小眾的數據集上刷指標刷排名。我想要指出的是，哪怕“遇事不決，量子力學；難題有疑，強化學習”，Deepseek-R1 等具有思維鏈的大模型的出現，使得我們人類可以以簡單地結果為導向，讓 LLM 以黑盒形式自己去思考挖掘需要哪些特征，需要如何提取這些特征。但是， 會嚴重加速“人類的懶惰性“ ！

我其實非常喜歡傳統計算機視覺，喜歡去理解當年如何建模這個問題的過程，如何讓問題回歸到數學或者物理的領域去，回歸到筆尖紙張上面去。盡管大模型具有自動特征提取和處理功能， 特征工程（具有數學依據的人工特征） 依然是十分重要和必要的。這部分能力不能丟，因為這其實也是人類發現問題、分析問題、解決問題的能力。

當算力和數據集有限的時候，我們的神經網絡模型不可能太復雜，導致模型的特征空間和解空間不大，這時候特征工程還能和神經網絡抗衡一下。隨著算力和數據集的提升，神經網絡參數越來越多，特征空間和解空間越來越大，這時候人類沒有 LLM 表現好，一方面是我們的特征空間和解空間就沒有LLM大，另一方面是我們暫時還沒有比 LLM 先找到一個更優解。

我不是讓大家從大模型時代往回走，而是說： 大模型時代，算力發展、數據標注和基礎理論都很重要！

我的原文地址：TGD第十篇：當神經網絡遇到TGD特征

---

1. D. Deng, Z. Chen, Y. Zhou, and B. E. Shi. MIMAMO net: Integrating micro- and macro-motion for video emotion recognition. In The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020, pages 2621–2628. AAAI Press, 2020. ??

2. 大概來說就是，首先獲得輸入幀經傅立葉變換后的頻域系數，將系數經過水平和豎直兩個方向的帶通濾波，再轉換到時域空間得到濾波后的相位，再將相鄰幀之間的相位做差表征時間維度的變化屬性。 ??

3. S. Zafeiriou, D. Kollias, M. A. Nicolaou, A. Papaioannou, G. Zhao, and I. Kotsia. Aff-wild: valence and arousal’in-the-wild’challenge. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pages 34–41, 2017. ??