奇異信號:信號與系統分析中,經常遇到函數本身有不連續點(跳變電)或其導函數與積分有不連續點的情況,這類函數稱為奇異函數或奇異信號,也稱之為突變信號。以下為一些常見奇異函數。
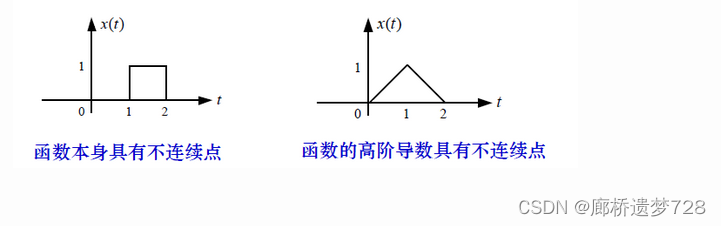
?單位斜變信號
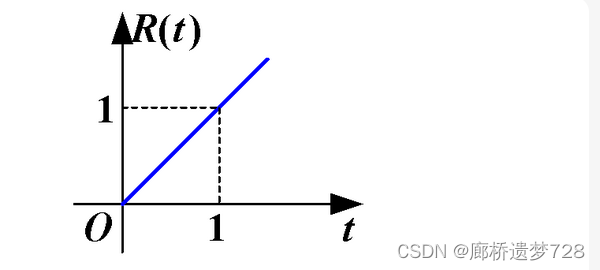
斜變信號也稱為斜坡信號或斜升信號,指某一時刻隨時間正比例增長的信號。如果增長率為1,就稱為單位斜變函數。
圖像與表達式如下:
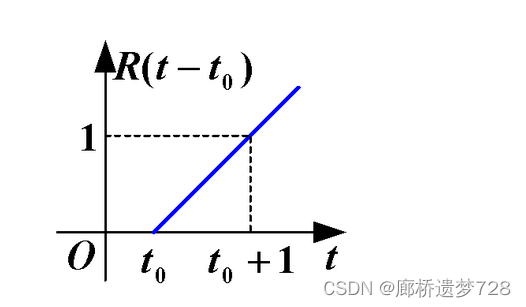
將起點移至t0,圖像與表達式為:
單位階躍函數
物理背景
在t=0時刻對某一電路接入單位電源,并且無限保持下去。單位階躍函數通常以符號u(t)表示。
表達式為:
如果電源接入時間延遲到t0,則為一個“延時的階躍函數”。即將起點移至t0,表達式為:
圖像分別如下所示,在跳變點處,函數值未定義(各不相同);或者在跳變處規定函數值為1/2
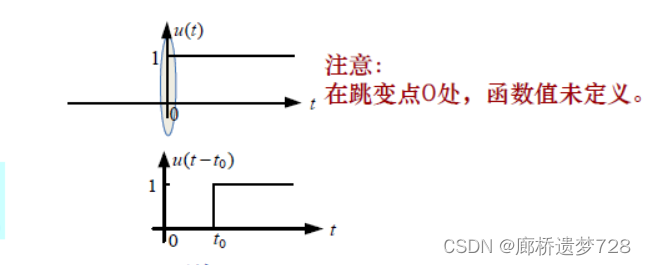
規定函數取極限的定義
給定一個如下的函數,求極限,便能得到階躍函數。

幾種定義
第一種定義:自變量為0時函數值不確定或不定義。
第二種定義:自變量為0時函數值為1/2。
第三種定義:自變量為0時,函數值為1。
階躍函數的性質(作用)
斜變函數求導
單位斜變函數的導數等于單位階躍函數,即df (t)/dt=u(t)。
表示矩形脈沖
用階躍信號及其延時信號之差來表示矩形脈沖。
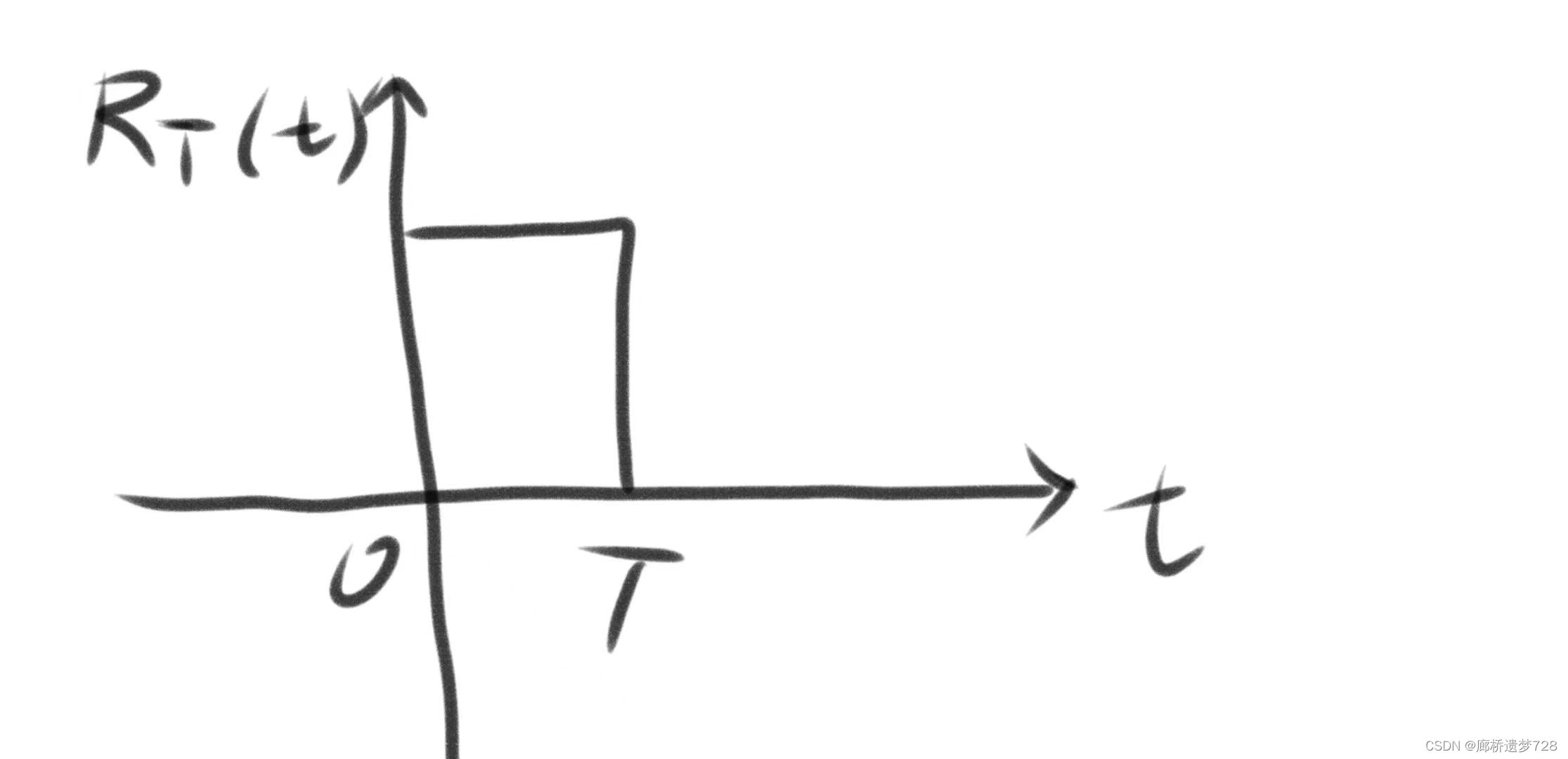
對于如下信號用RT(t)來表示,下標T表示矩形脈沖出現在0到T時刻之間。公式可表示為:RT(t)=u(t) - u(t-T)。
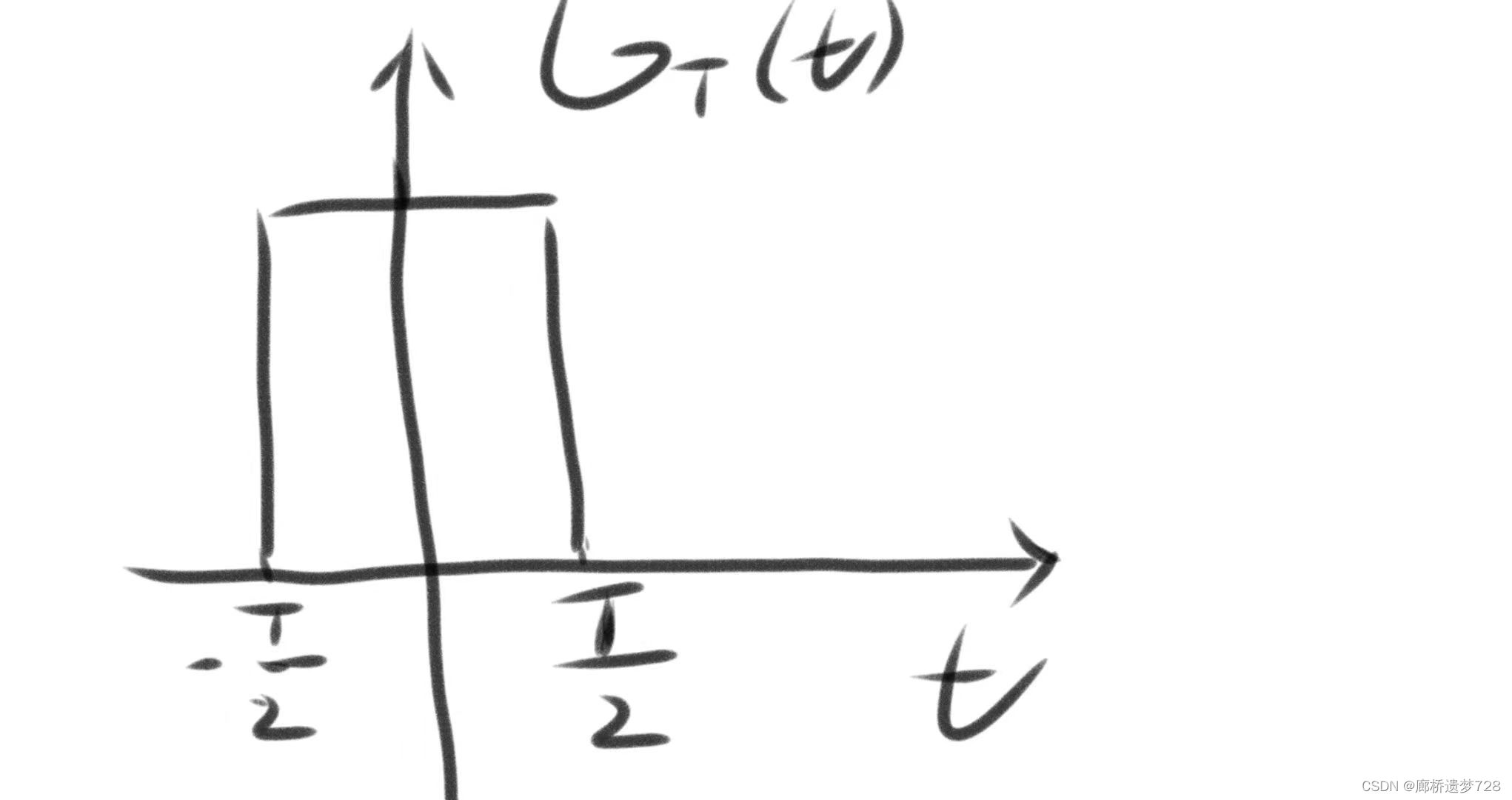
如果矩形脈沖對于縱坐標左右對稱,則以符號GT(t)來表示:GT(t)=u(t+T)-u(t-T)。下標表示其寬度。
表示分段常量信號

表示信號作用區間
利用階躍函數的單邊特性,即信號在某接入時刻t0以前的幅度為0。

積分
單位沖激信號
物理背景
某些物理現象需要用一個時間極短,但取值極大的函數來表示。例如中瞬間作用的沖擊力,電學中的電擊閃電等。沖激函數可用不同的方式來定義。圖形如下:
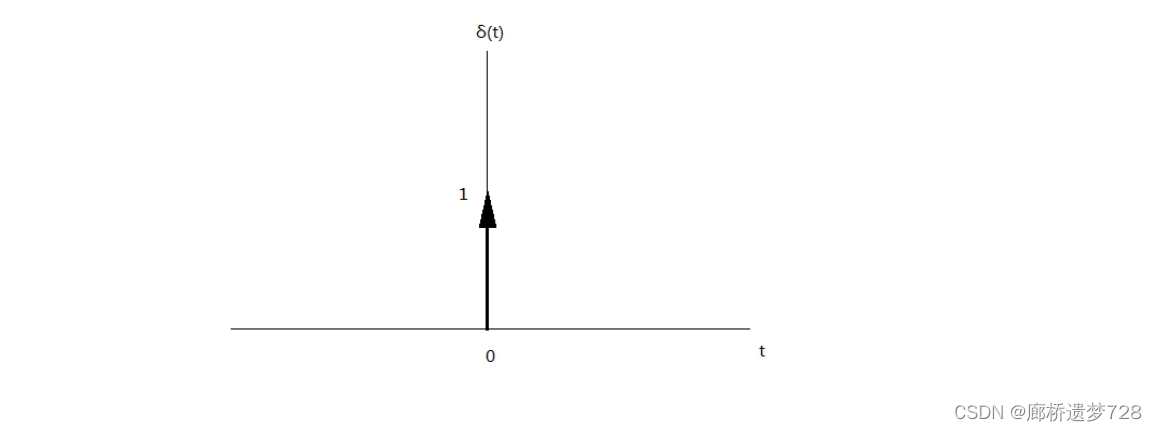
規定函數取極限定義
首先以矩形脈沖為例。有一個寬為 ,高位
的矩形脈沖,當保持矩形脈沖面積不變,而使寬趨近于0時,脈沖幅度必定為無窮大,此極限情況即為沖激函數,常記作:
如果矩形脈沖的面積不是固定為1,而是E,表示一個沖激強度為E倍單位值的沖激函數。(用圖形表示時,強度E注于箭頭旁)
規則函數系列的選型不限于矩形脈沖,也可用以下形式:三角形脈沖、雙邊指數脈沖、鐘形信號、Sa(t)信號(抽樣信號)等。
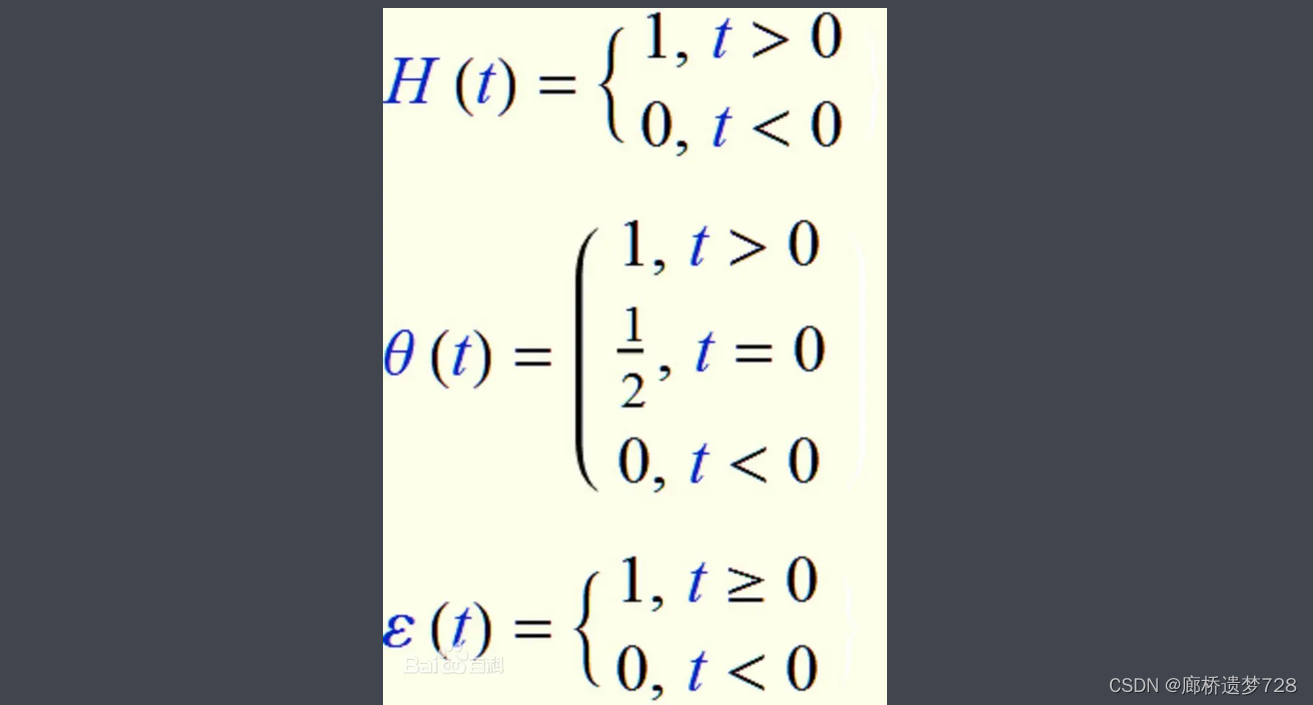
方法追加并顯示數據)





![[機緣參悟-158] :西游記中的“佛” 、“道”之爭](http://pic.xiahunao.cn/[機緣參悟-158] :西游記中的“佛” 、“道”之爭)





)
——堆排序)


)


