🔥 LeetCode 熱題 HOT 100

這里記錄下刷題過程中的心得，其實算法題基本就是個套路問題，很多時候你不知道套路或者模板，第一次嘗試去做的時候就會非常懵逼、沮喪和無助。而且就算你一時理解并掌握了，過一段時間往往會絕望的發現你又不會了。所以過遍數就非常重要，我目前配合 anki? 來復習。

?LC001two_sum 兩數之和（簡單）

. - 力扣（LeetCode）

題目：

給定一個整數數組?nums?和一個整數目標值?target，請你在該數組中找出?和為目標值?target? 的那?兩個?整數，并返回它們的數組下標。

解法：

使用HashMap 是比較常規的解法，這里有個技巧是只通過一遍循環就能解決問題。從頭開始遍歷，然后順便把元素放入HashMap，這樣就不用先遍歷一遍初始化HashMap。

public int[] twoSum(int[] nums, int target) {Map<Integer, Integer> cache = new HashMap<>();for (int i = 0; i < nums.length; i++) {int value = target - nums[i];if (cache.containsKey(value)) {return new int[]{ i, cache.get(value) };}cache.put(nums[i], i);}return null;}

LC002add_two_numbers 兩數相加（中等）

題目：

給你兩個 非空 的鏈表，表示兩個非負的整數。它們每位數字都是按照 逆序 的方式存儲的，并且每個節點只能存儲 一位 數字。

請你將兩個數相加，并以相同形式返回一個表示和的鏈表。

你可以假設除了數字 0 之外，這兩個數都不會以 0 開頭。

解法：

鏈表題通常的操作是先增加一個前置pre 節點，這樣就能大大方便后續的操作。因為最后你要返回頭節點，這個時候pre.next 就是。

這道題核心難點是對進位的處理，因此需要有一個變量表示每次的進位，同時在最后還要對進位進行判斷，這點特別容易遺漏。剩下的就是一些細節的處理，有一些為null 的情況需要處理，這點也非常容易踩坑。

 public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode pre = new ListNode(0);ListNode cur = pre;//表示進位int carry = 0;while (l1 != null || l2 != null) {int left = l1 == null ? 0 : l1.val;int right = l2 == null ? 0 : l2.val;int sum = left + right + carry;carry = sum / 10;sum = sum % 10;cur.next = new ListNode(sum);cur = cur.next;l1 = l1 == null ? null : l1.next;l2 = l2 == null ? null : l2.next;}if (carry == 1) {cur.next = new ListNode(carry);}return pre.next;}

LC003longest_substring 無重復字符的最長子串 （中等）

. - 力扣（LeetCode）

題目：

給定一個字符串 s ，請你找出其中不含有重復字符的 最長子串的長度

解法：

典型的滑動窗口策略，窗口的左右下標剛開始都是0，首先需要一個緩存用于存放已經遍歷過的字符。右下標開始遍歷，并跟緩存中的字符比較，存在就說明遇到重復的了，這個時候左右下標構成的字符串就是非重復的字符串，然后當前元素進緩存，左下標往前。這里需要注意要設置一個起始點，在每次判斷更新最大長度的時候需要記錄下這個起始點下標，不然最后輸出的時候沒辦法定位。

public int lengthOfLongestSubstring(String s) {Map<Character, Integer> cache = new HashMap<>();int left = 0, max = 0;for (int i = 0; i < s.length(); i++) {final char key = s.charAt(i);if (cache.containsKey(key)) {// 這里+1 說明遇到重復字母，left 標往前挪動了一位left = Math.max(left, cache.get(key) + 1);}cache.put(key, i);max = Math.max(max, i - left + 1);}return max;}

這里有個優化性能的小技巧，因為字符由由英文字母、數字、符號和空格組成，因此可以用asc2 表示，這樣可以用int[128] 代替HashMap。

LC004median_of_two?尋找兩個正序數組的中位數 （困難）

. - 力扣（LeetCode）

題目：

給定兩個大小分別為 m 和 n 的正序（從小到大）數組 nums1 和 nums2。請你找出并返回這兩個正序數組的 中位數 。

算法的時間復雜度應該為 O(log (m+n)) 。

解法：

難點在于復雜度要求為log，這個典型折半查找的思路了。

根據中位數的定義，當 m+n是奇數時，中位數是兩個有序數組中的第 (m+n)/2 個元素，當 m+n 是偶數時，中位數是兩個有序數組中的第 (m+n)/2 個元素和第 (m+n)/2+1 個元素的平均值。因此，這道題可以轉化成尋找兩個有序數組中的第 k 小的數，其中 k 為 (m+n)/2 或 (m+n)/2+1。

剩下的問題就是怎么在兩個數組中找第k個數，并且還要是log 的復雜度。這里直接給結論，先比較兩個數組中k/2 位置的2個數，小的那一個所在數組前k/2 就可以舍棄了，同樣的思路接著找剩下的k/2，當然這里有很多細節和邊界需要考慮。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {int length1 = nums1.length, length2 = nums2.length;int totalLength = length1 + length2;//個數為奇數的情況if (totalLength % 2 == 1) {int midIndex = totalLength / 2;double median = getKthElement(nums1, nums2, midIndex + 1);return median;} else {//個數偶數的情況int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;double median =(getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;return median;}}/*** 注意這里的k是第k位，并不是下標k** @param nums1* @param nums2* @param k* @return*/public int getKthElement(int[] nums1, int[] nums2, int k) {/* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 進行比較* 這里的 "/" 表示整除* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共計 k/2-1 個* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共計 k/2-1 個* 取 pivot = min(pivot1, pivot2)，兩個數組中小于等于 pivot 的元素共計不會超過 (k/2-1) + (k/2-1) <= k-2 個* 這樣 pivot 本身最大也只能是第 k-1 小的元素* 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把這些元素全部 "刪除"，剩下的作為新的 nums1 數組* 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把這些元素全部 "刪除"，剩下的作為新的 nums2 數組* 由于我們 "刪除" 了一些元素（這些元素都比第 k 小的元素要小），因此需要修改 k 的值，減去刪除的數的個數*/int length1 = nums1.length, length2 = nums2.length;int index1 = 0, index2 = 0;while (true) {// 邊界情況if (index1 == length1) {return nums2[index2 + k - 1];}if (index2 == length2) {return nums1[index1 + k - 1];}if (k == 1) {return Math.min(nums1[index1], nums2[index2]);}// 正常情況int half = k / 2;int newIndex1 = Math.min(index1 + half, length1) - 1;int newIndex2 = Math.min(index2 + half, length2) - 1;int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];if (pivot1 <= pivot2) {k -= (newIndex1 - index1 + 1);index1 = newIndex1 + 1;} else {k -= (newIndex2 - index2 + 1);index2 = newIndex2 + 1;}}}

getKthElement 可以用遞歸的方法改寫下，這樣能精簡不少。

LC005longest_palindromic?最長回文子串 （中等）

. - 力扣（LeetCode）

題目：

給你一個字符串 s，找到 s 中最長的回文子串。如果字符串的反序與原始字符串相同，則該字符串稱為回文字符串。

解法：

這里用了動態規劃，動態規劃的難點在于動態方程的推導，動態方程很多時候又取決于動態數組的定義，只能說多接觸不同類型的題目來增長這方面的經驗。

針對這道題定義了boolean 類型的2維數組，dp[i][j] 表示s[i][j]是否為回文。

然后就是2層循環不斷推進的過程。

public String longestPalindrome(String s) {final int len = s.length();if (len < 2) {return s;}int begin = 0, max = 1;//dp[i][j] 表示s[i][j]是否為回文boolean[][] dp = new boolean[len][len];final char[] charArray = s.toCharArray();for (int j = 0; j < len; j++) {for (int i = 0; i <= j; i++) {if (charArray[j] == charArray[i]) {//只有3個的時候，只要兩邊相等就是回文if (j - i < 3) {dp[i][j] = true;} else {//大于3個的時候就要看進一步的情況dp[i][j] = dp[i + 1][j - 1];}}//如果是回文就看下是否當前最大if (dp[i][j] && j - i + 1 > max) {begin = i;max = j - i + 1;}}}return s.substring(begin, begin + max);}

LC011container_with?盛最多水的容器 （中等）

. - 力扣（LeetCode）

題目：

給定一個長度為 n 的整數數組 height 。有 n 條垂線，第 i 條線的兩個端點是 (i, 0) 和 (i, height[i]) 。找出其中的兩條線，使得它們與 x 軸共同構成的容器可以容納最多的水。返回容器可以儲存的最大水量。

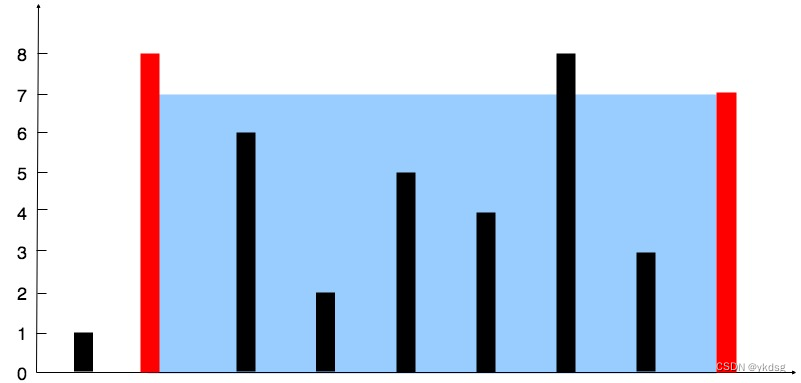
解法：

套路題，用雙指針左右夾逼法求解。一開始左右指針在兩邊頭尾，這個時候寬度是最大的，高是兩邊最矮的那個，然后進一步從矮的那邊往中間靠近。

public int maxArea(int[] height) {int left = 0, right = height.length - 1;int max = 0;while (left < right) {int high = Math.min(height[left], height[right]);int wide = right - left;max = Math.max(max, high * wide);if (height[left] < height[right]) {left++;} else {right--;}}return max;}

未完待續