參考資料：用python動手學統計學

????????概率分布為泊松分布、聯系函數為對數函數的廣義線性模型叫作泊松回歸。解釋變量可以有多個，連續型和分類型的解釋變量也可以同時存在。

1、案例說明

? ? ? ? 分析不同氣溫與啤酒銷量的關系。構造不同氣溫下的銷量的數學模型，其線性預測算子如下：

? ? ? ? 如果聯系函數為對數函數，則啤酒銷量與氣溫的關系如下：

? ? ? ? 對兩邊取指數，變形如下：

2、導入庫

# 導入庫
# 用于數值計算的庫
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于繪圖的庫
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 用于估計統計模型的庫
import statsmodels.formula.api as smf
import statsmodels.api as sm

3、數據準備

beer_num=[ 6, 11,  2,  4,  2,  2,  3,  5,  6,  7,  6, 11,  4, 16,  4, 13,  5,  7,  3,  5, 14, 22,  7, 11, 18, 17,  2,  2,  4, 16]
temp=[17.5, 26.6,  5. , 14.1,  9.4,  7.8, 10.6, 15.4, 16.9, 21.2, 17.6, 25.6, 11.1, 31.3,  5.8, 25.1, 17.5, 21.8,  9.2, 10.9, 29. , 34. , 14.4, 25.8, 31.3, 31.8,  7.6,  6.2, 10.1, 31.3]
beer=pd.DataFrame({'beer_num':beer_num,'temp':temp
})
beer.head()

4、泊松回歸擬合

mod_pois=smf.glm('beer_num~temp',data=beer,family=sm.families.Poisson()).fit()
mod_pois.summary()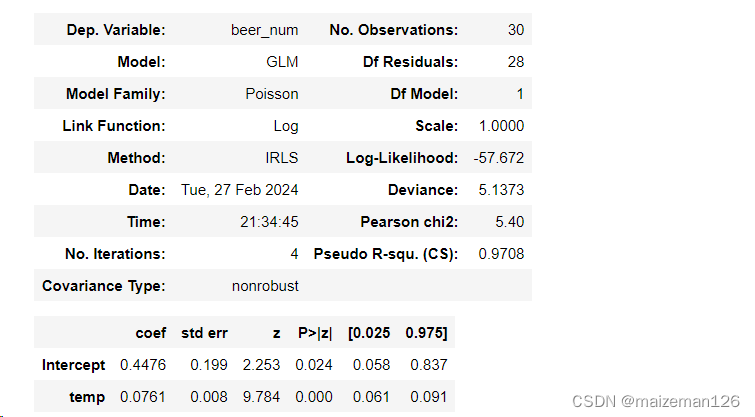

5、模型的選擇

# 擬合空模型
mod_pois_null=smf.glm('beer_num~1',data=beer,family=sm.families.Poisson()).fit()
# 輸出mod_pois_null和mod_pois的AIC
print('空模型：',mod_pois_null.aic.round(3))
print('氣溫模型：',mod_pois.aic.round(3))

? ? ? ? 兩個模型相比，包含氣溫變量的模型的AIC更小，說明氣溫這個解釋變量時必要的。

6、回歸曲線

? ? ? ? seaborn中的函數無法直接繪制出泊松回歸的曲線，因而這里把所估計的模型的預測值繪制成散點圖。

# 計算預測值
x=np.arange(0,37,1)
pred=mod_pois.predict(pd.DataFrame({'temp':x}))
# 繪制散點圖
plt.scatter(x=beer.temp,y=beer.beer_num)
# 繪制預測曲線
plt.plot(x,pred)
# 添加坐標軸標題
plt.xlabel('temperature')
plt.ylabel('beer_numbers')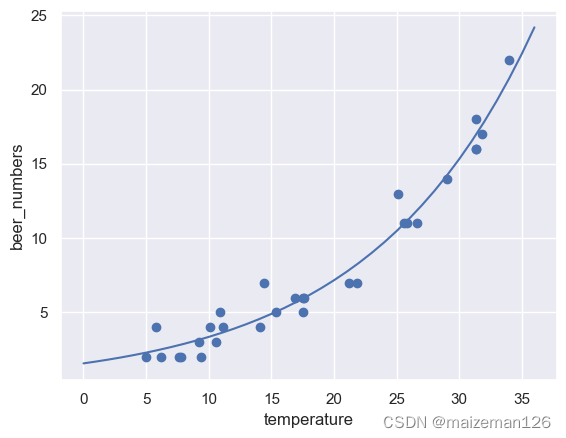

7、泊松回歸中回歸系數的含義

? ? ? ? 泊松回歸的聯系函數為對數函數，對數的一個性質就是把加法變成乘法。在正態線性模型中，回歸系數的含義是：x每增加一個單位，y增加系數個單位。而在泊松回歸中，x每增加一個單位，y變為原來的多少倍。