一、范式總結

第一步,先求候選碼,由此得到:主屬性、非主屬性。
二、判斷部分函數依賴的技巧
【回顧】:部分函數依賴
(X,Y)——>Z;
X——>Z 或者 Y——>Z
題型:給出函數依賴集和屬性,判斷該關系模式屬于第幾范式。
(一般題目中給出的屬性都是原子的,不可再分的。)
示例:

求出候選碼
若是候選碼為屬性的組合,則可能有部分函數依賴;(存在部分函數依賴,1NF)
若是候選碼是單個屬性,一定沒有部分函數依賴。
三、判斷傳遞函數依賴的技巧?
【回顧】傳遞函數依賴
示例:

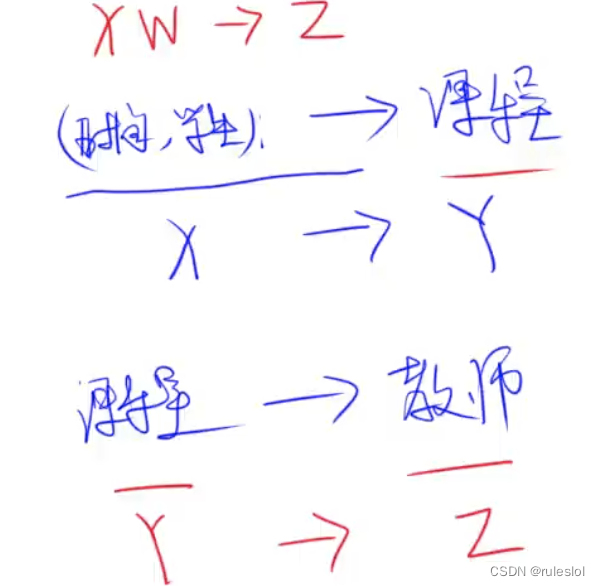
存在傳遞函數依賴,所以是第二范式。
候選碼,一定是偽傳遞率中的 X!
四、真題?
真題1:

沒有部分函數依賴,沒有傳遞函數依賴 = 3NF
真題2:

真題3:

真題4:

真題5:

真題6:

五、關系分解的真題?
真題1:(了解即可)
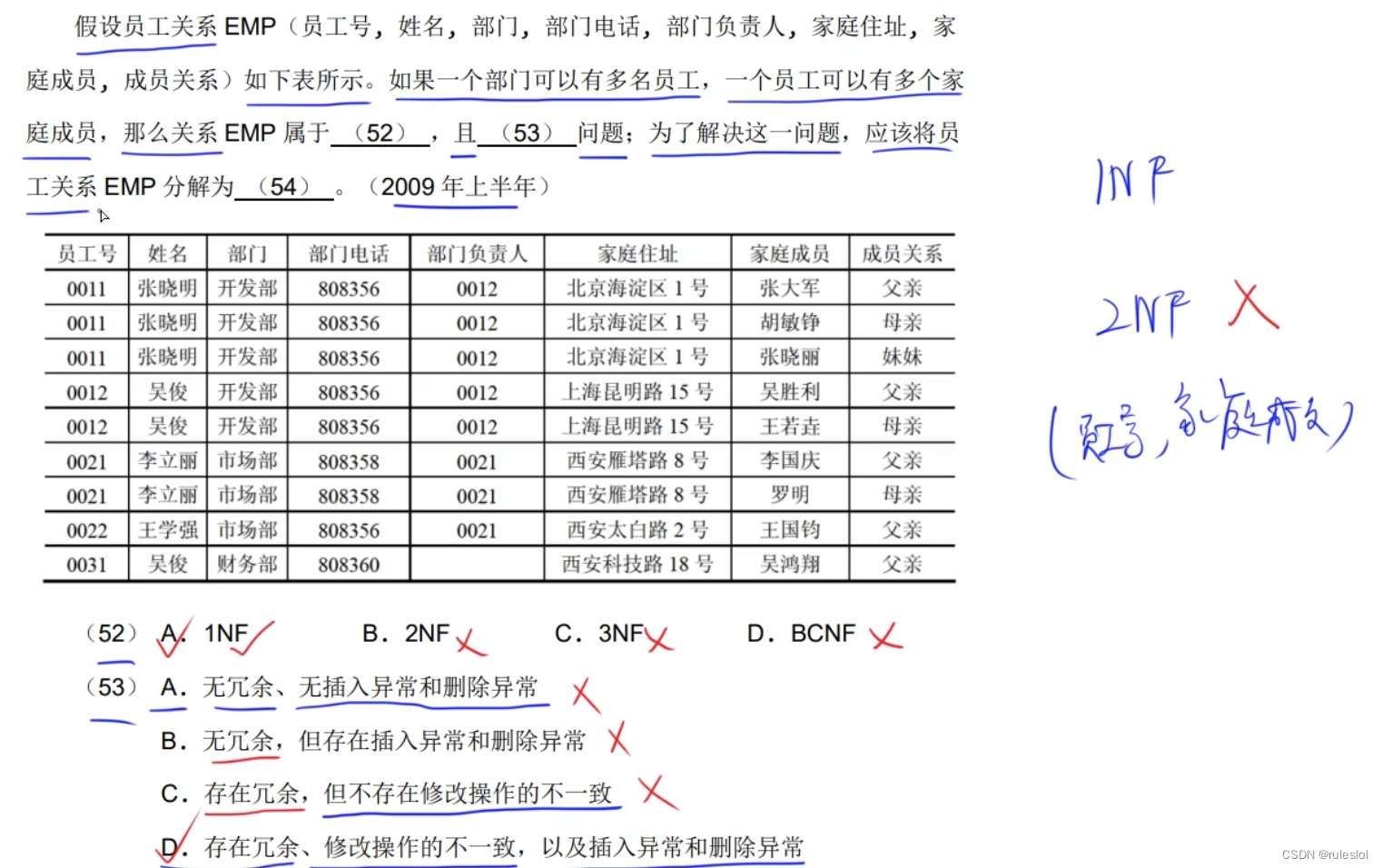

【回顧】部分函數依賴的規范化:(此時分解后,可能存在傳遞函數依賴)
若(X,Y)——> Z;X——>A,X——>B,X——>C,Y——>D,Y——>E
1、將所有依賴于X的所有非主屬性,加上X,一起移出來。X、A、B、C(原表保留X,為了將原本的函數依賴保持住)
2、將所有依賴于Y的所有非主屬性,加上Y,一起移出來。Y、D、E(原表保留Y,為了將原本的函數依賴保持住)
3、(X,Y)——> Z:X、Y、Z;(為了將原本的函數依賴保持住)
【回顧】傳遞函數依賴,規范化:
若:X——>Y,Y——>Z1,Y——>Z2;(X,Y,Z1,Z2)
將Y和Y決定的屬性都移出原表,原表要保留Y
(X,Y)、(Y,Z1,Z2)
真題2:
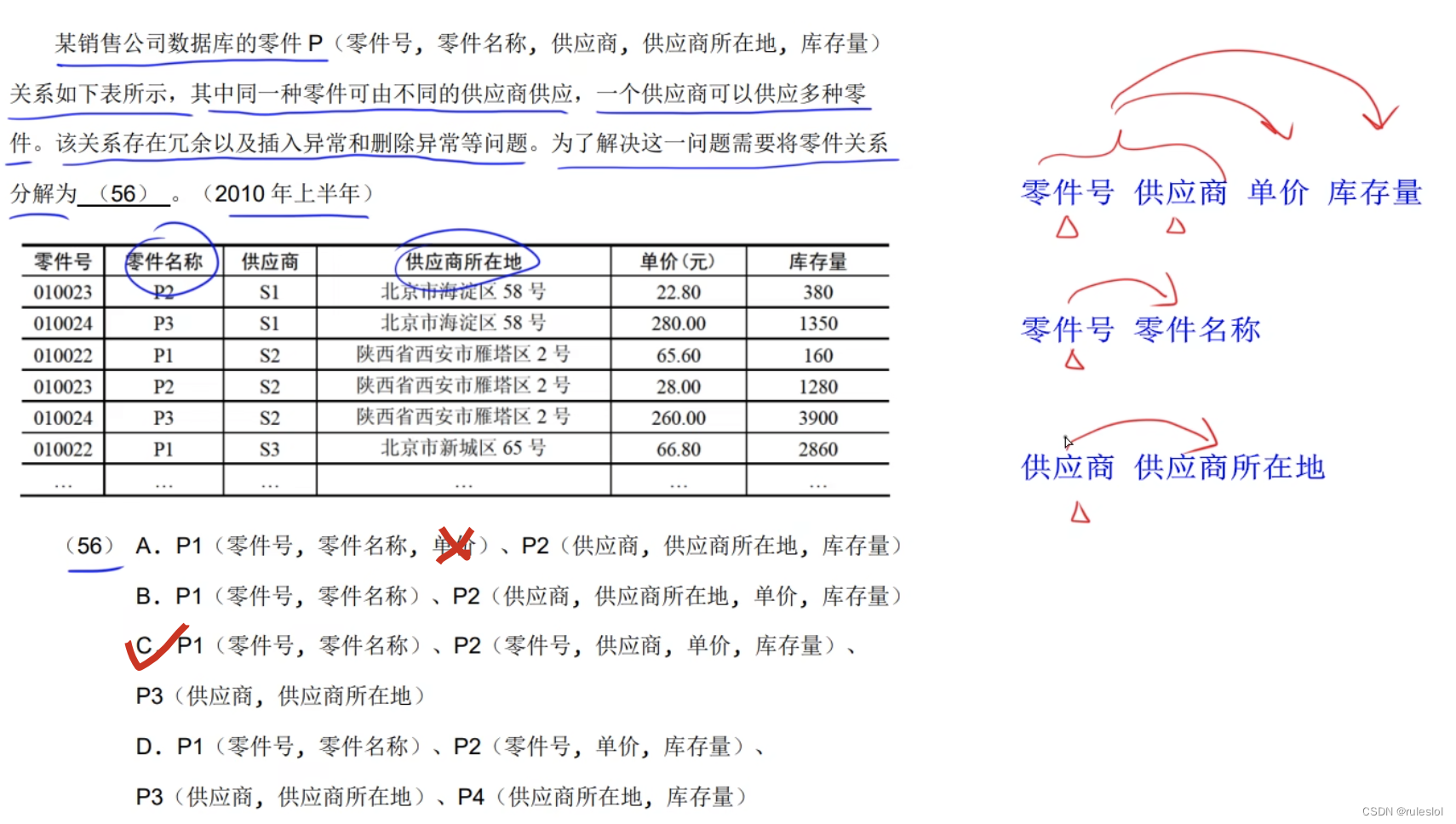
真題3:

六、無損連接、保持函數依賴的真題
6-1、無損連接的定義

若:R關系,分解為:R1,R2,R3關系
將?R1,R2,R3關系自然連接,去掉重復屬性,看是否 = 原來的屬性U。
【注意】:
R1,R2,R3中要有重復屬性列,否則,自然連接為空集!!!
6-2、保持函數依賴的定義

6-3、真題
真題1:

真題2:D

真題3:

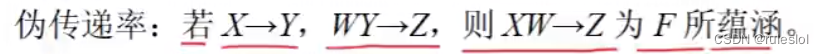








![[VSCode插件] 輕量級靜態博客 - MDBlog](http://pic.xiahunao.cn/[VSCode插件] 輕量級靜態博客 - MDBlog)
![[electron雜項] 記錄學習electron碰到問題(持續更新)](http://pic.xiahunao.cn/[electron雜項] 記錄學習electron碰到問題(持續更新))







)


