一：哈希表

一般哈希表都是用來快速判斷一個元素是否出現集合里。

直白來講其實數組就是一張哈希表，哈希表中關鍵碼就是數組的索引下標，然后通過下標直接訪問數組中的元素。

1.兩數之和

題目鏈接：. - 力扣（LeetCode）

// 哈希表
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map <int, int> map;for(int i = 0; i < nums.size(); i++){auto iter = map.find(target - nums[i]);if(iter != map.end()){return {iter->second, i};}else{map.insert(pair<int, int>(nums[i], i));}}return {};}
};

本題其實有四個重點：

• 為什么會想到用哈希表

本題呢，我就需要一個集合來存放我們遍歷過的元素，然后在遍歷數組的時候去詢問這個集合，某元素是否遍歷過，也就是 是否出現在這個集合。那么我們就應該想到使用哈希法了。

• 哈希表為什么用map

這道題目中并不需要key有序，選擇std::unordered_map 效率更高！

• 本題map是用來存什么的

map目的用來存放我們訪問過的元素，因為遍歷數組的時候，需要記錄我們之前遍歷過哪些元素和對應的下標，這樣才能找到與當前元素相匹配的（也就是相加等于target）

• map中的key和value用來存什么的

這道題 我們需要 給出一個元素，判斷這個元素是否出現過，如果出現過，返回這個元素的下標。

那么判斷元素是否出現，這個元素就要作為key，所以數組中的元素作為key，有key對應的就是value，value用來存下標。

所以 map中的存儲結構為 {key：數據元素，value：數組元素對應的下標}。

?2. 字母異位詞分組

class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {map<string, int> myhash;vector<vector<string>> myAns;int cint =0;for(int i = 0; i<strs.size(); i++){string temString = strs[i];sort(temString.begin(), temString.end());auto iter = myhash.find(temString);if(iter == myhash.end()){myAns.push_back(vector<string>());myAns.back().push_back(strs[i]);myhash[temString]=cint;cint ++;}else{int index = myhash[temString];myAns[index].push_back(strs[i]);}}return myAns;}
};

?3.最長連續序列

class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> myset;for(const int& num : nums){myset.insert(num);}int longestStreak = 0;for(const int& num : myset){if(myset.count(num-1) == 0){int currentNum = num;int currentStreak = 1;while(myset.count(currentNum +1)){currentNum = currentNum + 1;currentStreak = currentStreak + 1; }longestStreak = max(longestStreak, currentStreak);}}return longestStreak;}
};

?二：雙指針

1.移動零

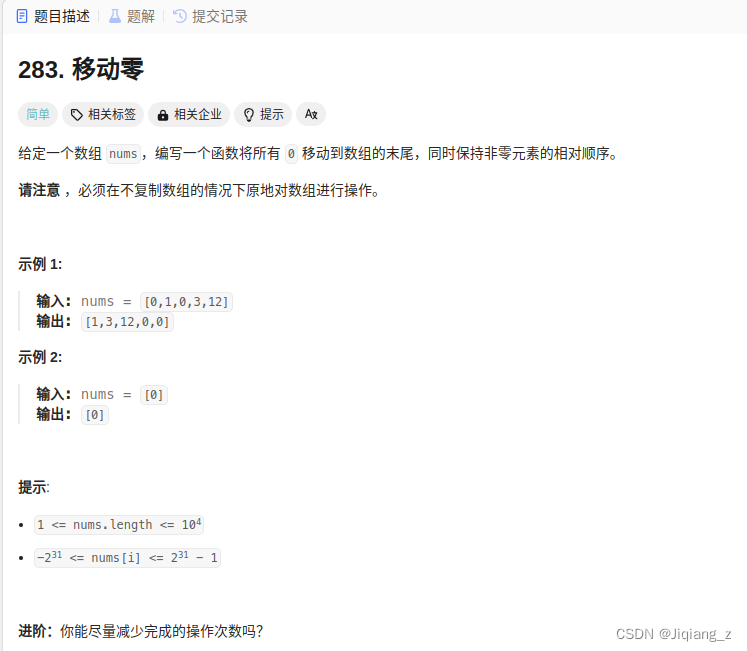
// 使用雙指針，左指針指向當前已經處理好的序列的尾部，右指針指向待處理序列的頭部。
// 右指針不斷向右移動，每次右指針指向非零數，則將左右指針對應的數交換，同時左指針右移
class Solution {
public:void moveZeroes(vector<int>& nums) {int n = nums.size(), left = 0, right = 0;while (right < n) {if (nums[right]) {swap(nums[left], nums[right]);left++;}right++;}}
};

思路：通過右指針來遍歷數組，左指針始終指向處理好的序列的尾部。

?2.盛最多水的容器

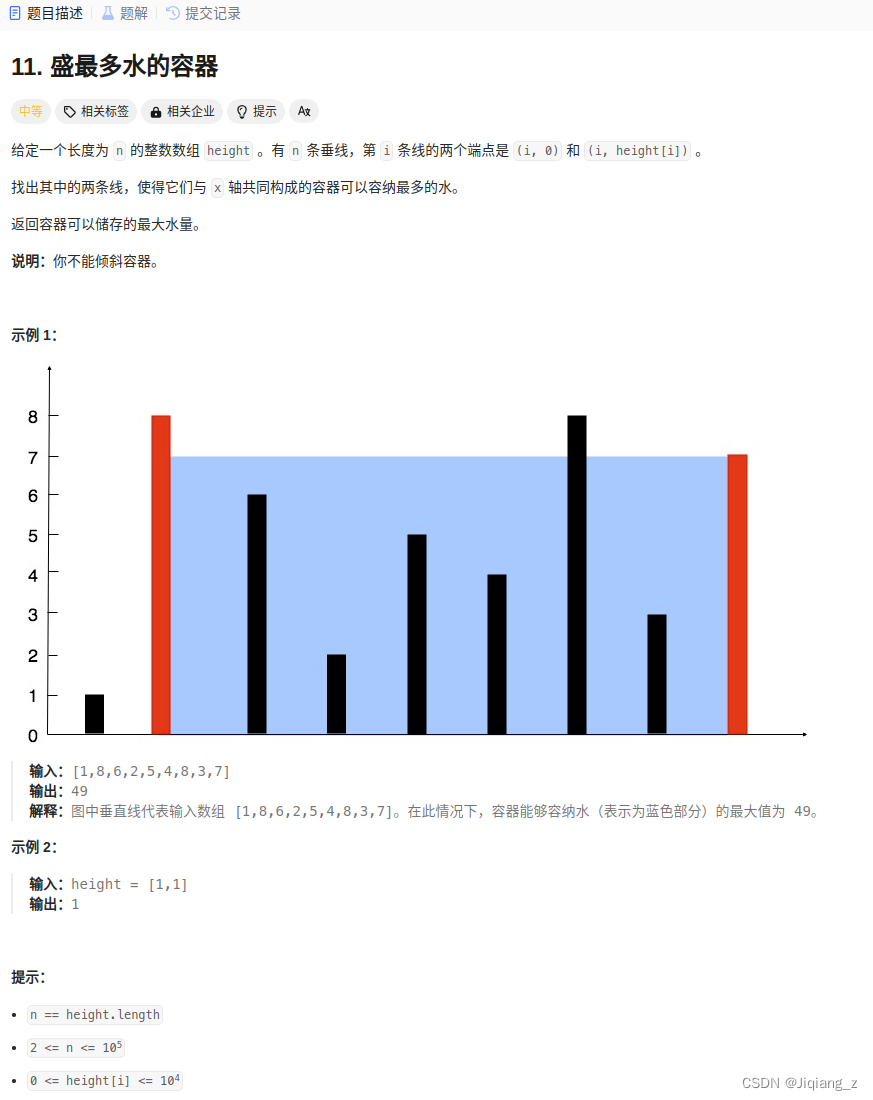
/* 算法流程：
1.初始化： 雙指針 i , j 分列水槽左右兩端；
2.循環收窄： 直至雙指針相遇時跳出；a.更新面積最大值 res；b.選定兩板高度中的短板，向中間收窄一格；
3.返回值： 返回面積最大值 res 即可； */class Solution {
public:int maxArea(vector<int>& height) {int i = 0, j = height.size() - 1, res = 0;while(i < j) {res = height[i] < height[j] ? max(res, (j - i) * height[i++]): max(res, (j - i) * height[j--]); }return res;}
};

3.三數之和

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(), nums.end());// 找出a + b + c = 0// a = nums[i], b = nums[left], c = nums[right]for (int i = 0; i < nums.size(); i++) {// 排序之后如果第一個元素已經大于零，那么無論如何組合都不可能湊成三元組，直接返回結果就可以了if (nums[i] > 0) {return result;}// 錯誤去重a方法，將會漏掉-1,-1,2 這種情況/*if (nums[i] == nums[i + 1]) {continue;}*/// 正確去重a方法if (i > 0 && nums[i] == nums[i - 1]) {continue;}int left = i + 1;int right = nums.size() - 1;while (right > left) {// 去重復邏輯如果放在這里，0，0，0 的情況，可能直接導致 right<=left 了，從而漏掉了 0,0,0 這種三元組/*while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;*/if (nums[i] + nums[left] + nums[right] > 0) right--;else if (nums[i] + nums[left] + nums[right] < 0) left++;else {result.push_back(vector<int>{nums[i], nums[left], nums[right]});// 去重邏輯應該放在找到一個三元組之后，對b 和 c去重while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;// 找到答案時，雙指針同時收縮right--;left++;}}}return result;}
};

?思路：

首先將數組排序，然后有一層for循環，i從下標0的地方開始，同時定一個下標left 定義在i+1的位置上，定義下標right 在數組結尾的位置上。

依然還是在數組中找到 abc 使得a + b +c =0，我們這里相當于 a = nums[i]，b = nums[left]，c = nums[right]。

接下來如何移動left 和right呢， 如果nums[i] + nums[left] + nums[right] > 0 就說明 此時三數之和大了，因為數組是排序后了，所以right下標就應該向左移動，這樣才能讓三數之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 說明 此時 三數之和小了，left 就向右移動，才能讓三數之和大一些，直到left與right相遇為止。

4.接雨水?

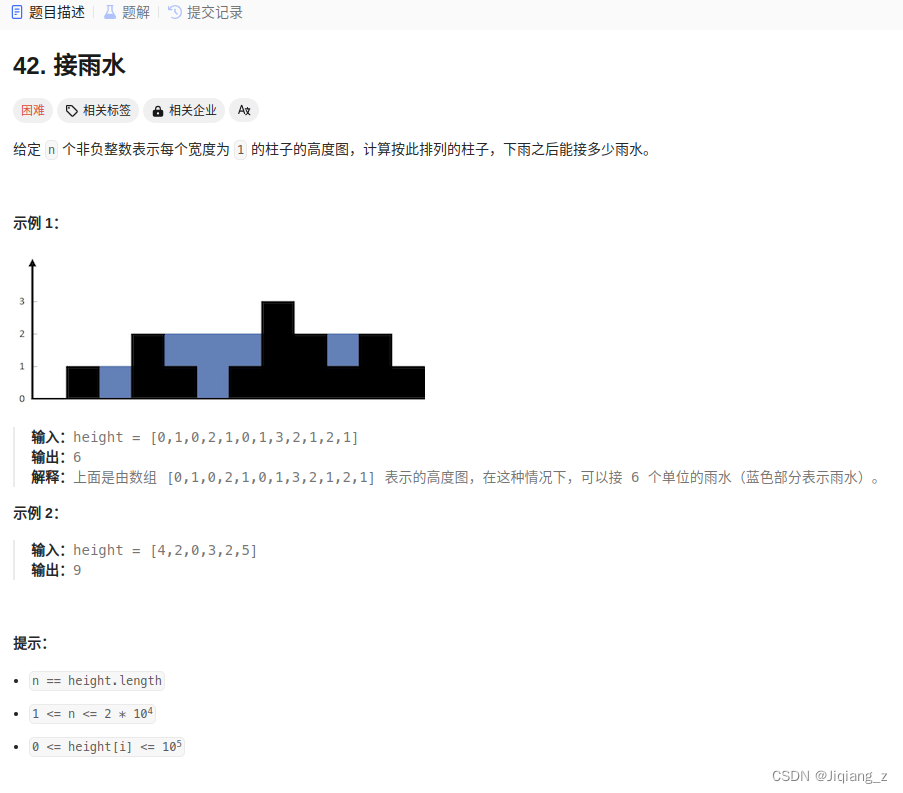
class Solution {
public:int trap(vector<int>& height) {int ans = 0;int left = 0, right = height.size() - 1;int leftMax = 0, rightMax = 0;while (left < right) {leftMax = max(leftMax, height[left]);rightMax = max(rightMax, height[right]);if (height[left] < height[right]) {ans += leftMax - height[left];++left;} else {ans += rightMax - height[right];--right;}}return ans;}
};