C++學習筆記:二叉搜索樹

二叉搜索樹

  • 什么是二叉搜索樹?
  • 搜索二叉樹的操作
    • 查找
    • 插入
    • 刪除
  • 二叉搜索樹的應用
  • 二叉搜索樹的代碼實現
    • K模型:
    • KV模型
  • 二叉搜索樹的性能怎么樣?

什么是二叉搜索樹?

二叉搜索樹又稱二叉排序樹，它或者是一棵空樹，或者是具有以下性質的二叉樹:

  • 若它的左子樹不為空，則左子樹上所有節點的值都小于根節點的值
  • 若它的右子樹不為空，則右子樹上所有節點的值都大于根節點的值
  • 它的左右子樹也分別為二叉搜索樹

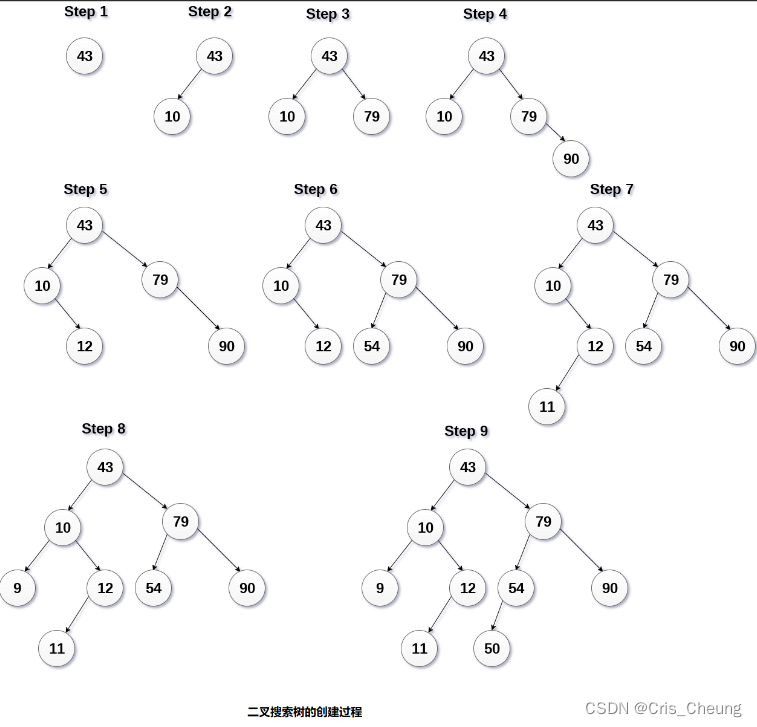
在這里插入圖片描述
由上圖可明顯得知搜索二叉樹的構建方式

搜索二叉樹的操作

這里插入一個搜索二叉樹為樣例:
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
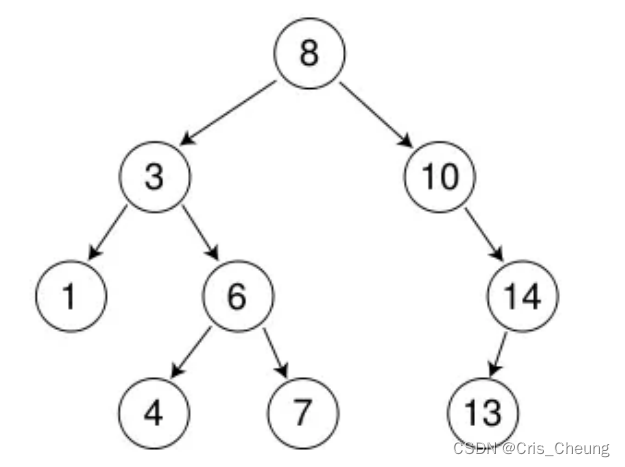
在這里插入圖片描述

查找

  • 從根開始比較，查找，比根大則往右邊走查找，比根小則往左邊走查找。
  • 最多查找高度次，走到到空，還沒找到，則這個值不存在

插入

  • 當這個樹為空樹時不用多說直接插入成根節點_root
  • 當這個樹不為空時,先找到所插入節點的位置,再進行插入
    比如要在下面這棵搜索樹中插入9
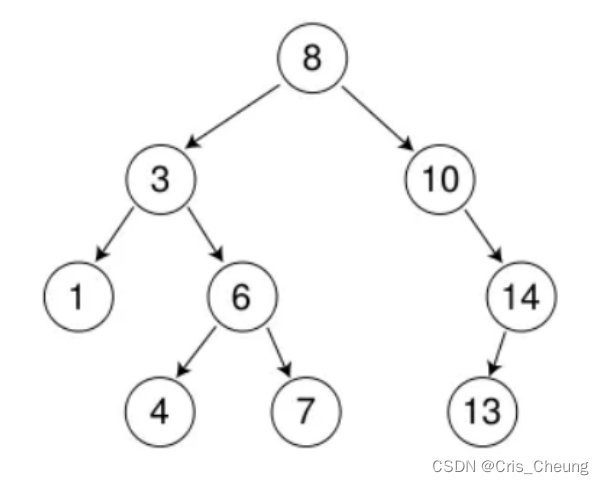
    在這里插入圖片描述

可以看出,9的位置應該在10的左子樹位置:
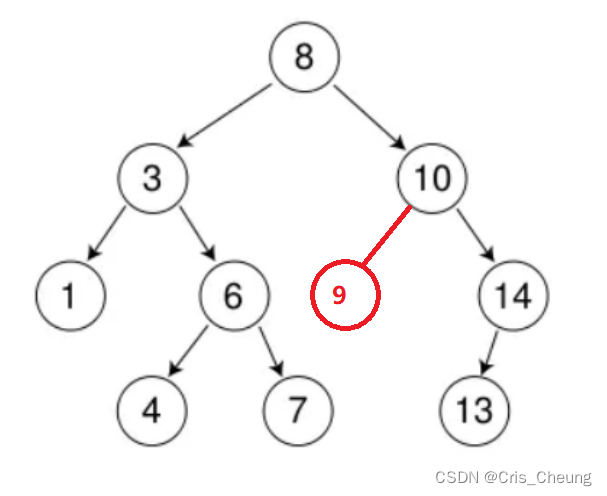
在這里插入圖片描述

在數據結構上這樣就算成功插入

刪除

首先查找元素是否在二叉搜索樹中，如果不存在，則返回false,否則要刪除的結點可能分下面幾種情況:

  1. 當這個節點是葉子節點或者只有左孩子時,先讓父節點指向該節點的左孩子,再刪除掉該節點–直接刪除
  2. 當這個節點是葉子節點或者只有右孩子時,先讓父節點指向該節點的右孩子,再刪除掉該節點–直接刪除
  3. 這個節點既有左子樹又有右子樹,則先將該節點的左子樹鏈接到右子樹的最左節點,再用右子樹來替換該節點–替換法刪除

前兩種情況都好說,例如刪除下列節點中的 7 和 14:
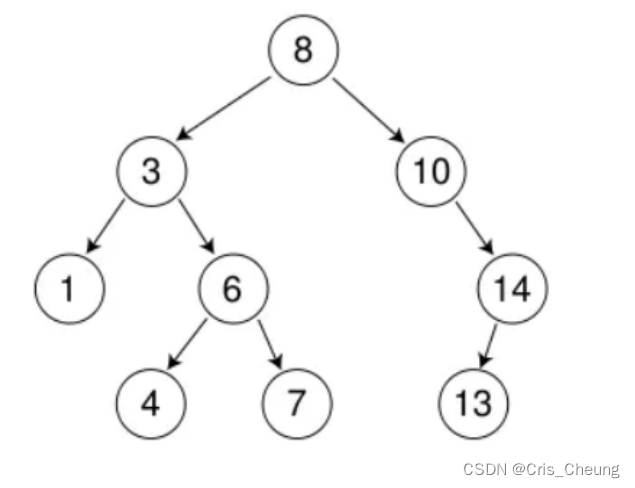
在這里插入圖片描述

刪7:直接刪除
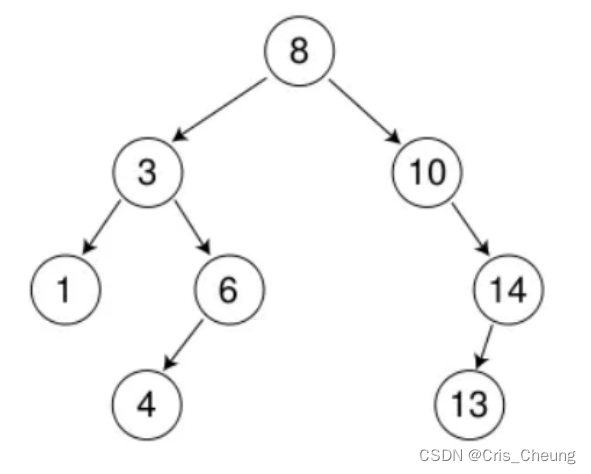
在這里插入圖片描述
刪14:刪掉14并將14的左子樹鏈接到10的右子樹
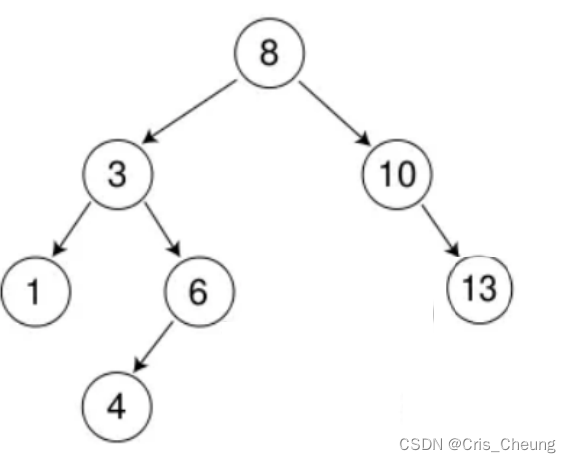
在這里插入圖片描述

比較復雜的是最后一種情況:當要刪除的節點既有左子樹又有右子樹的時候,則需要進行一些特殊調整,例如,刪除下面這顆樹中的3 和 8 時:
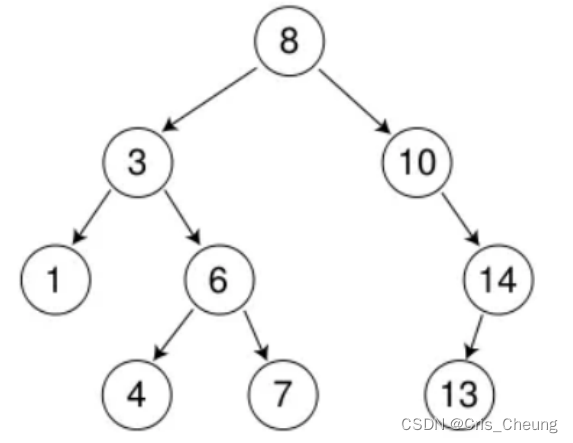
在這里插入圖片描述

刪除3,使用上述的第三種方法:
先將該節點的左子樹鏈接到右子樹的最左節點,再用右子樹來替換該節點
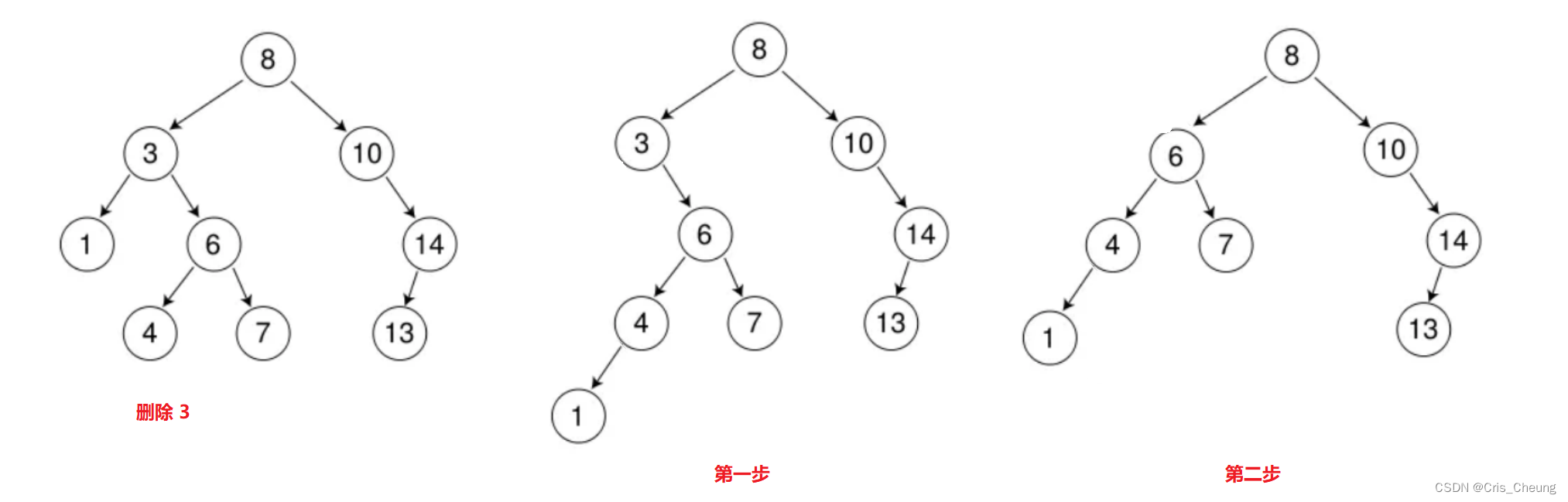
在這里插入圖片描述
刪除 8 ,使用上述的第三種方法:
先將該節點的左子樹鏈接到右子樹的最左節點,再用右子樹來替換該節點
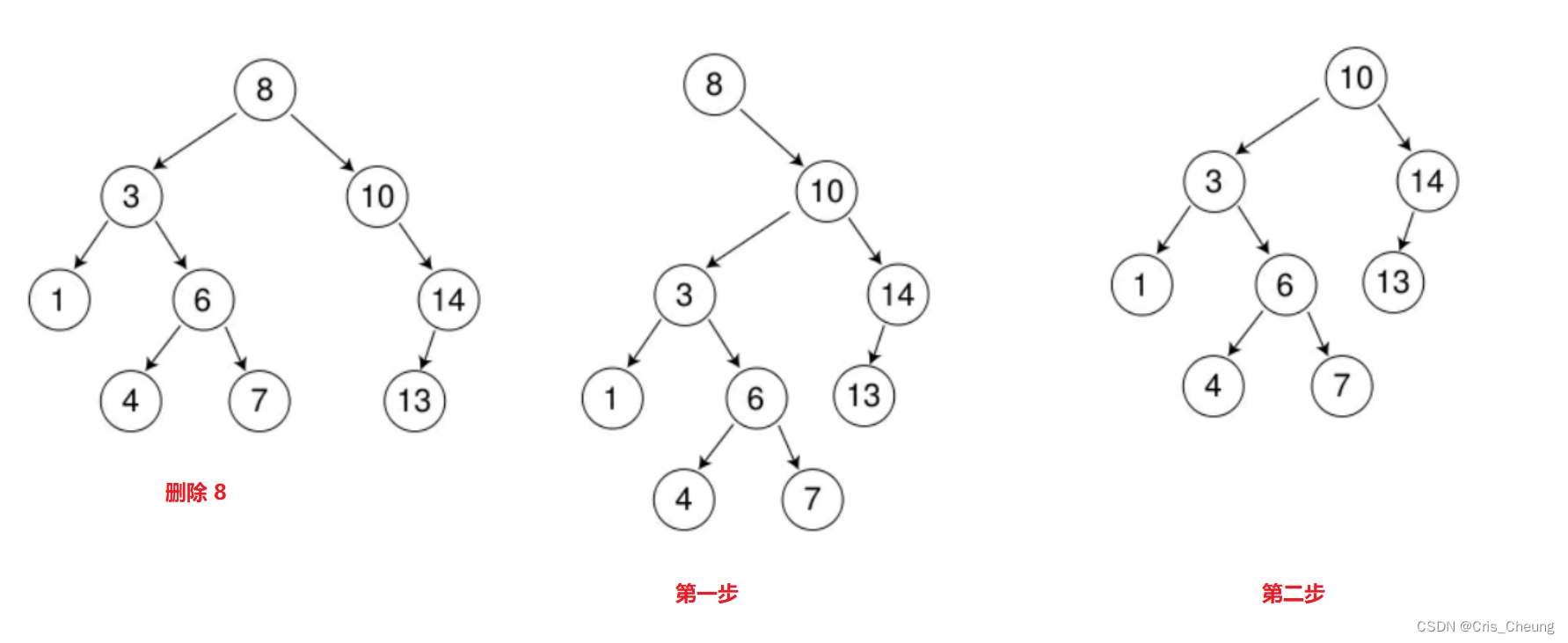
在這里插入圖片描述

以上就是二叉搜索樹的插入和刪除的主要思想,接下來是具體實現

二叉搜索樹的應用

二叉搜索樹分為兩種模型,一種是單鍵值的K模型,另一種是擁有鍵值對的KV模型,而后面需要學習的map,AVL樹等都會涉及到KV模型.

  1. K模型：K模型即只有key作為關鍵碼，結構中只需要存儲Key即可，關鍵碼即為需要搜索到的值。
    比如：給一個單詞word，判斷該單詞是否拼寫正確，具體方式如下：
  • 以詞庫中所有單詞集合中的每個單詞作為key，構建一棵二叉搜索樹
  • 在二叉搜索樹中檢索該單詞是否存在，存在則拼寫正確，不存在則拼寫錯誤。
  1. KV模型：每一個關鍵碼key，都有與之對應的值Value，即<Key, Value>的鍵值對。該種方式在現實生活中非常常見：
  • 比如英漢詞典就是英文與中文的對應關系，通過英文可以快速找到與其對應的中文，英文單詞與其對應的中文<word, chinese>就構成一種鍵值對；
  • 再比如統計單詞次數，統計成功后，給定單詞就可快速找到其出現的次數，單詞與其出現次數就是<word, count>就構成一種鍵值對

二叉搜索樹的代碼實現

K模型:

#pragma once#include<iostream>using namespace std;//單鍵值的搜索二叉樹  K模型
template <class K>
struct BSTNode
{BSTNode<K>* _left;BSTNode<K>* _right;K _key;BSTNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>
class BSTree
{
public:typedef BSTNode<K> Node;bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = cur;while (cur){parent = cur;if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool Find(const K& key){if (_root == nullptr)return false;Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{cout << " 存在" << endl;return true;}}return false;}bool Erase(const K& key){//空樹返回falseif (_root == nullptr)return false;//尋找keyNode* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){//這里注意一下,一定要往下一步走的時候父節點才隨著改變parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了 分情況//要刪除的節點左孩子或右孩子為空//左孩子為空if (cur->_left == nullptr){//若刪除的是根節點if (cur == _root){_root = cur->_right;}//不是跟節點else{//判斷當前節點是父節點的左孩子還是右孩子if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}//刪除delete cur;}//右孩子為空else if (cur->_right == nullptr){//若刪除的是根節點if (cur == _root){_root = cur->_left;}//不是跟節點else{//判斷當前節點是父節點的左孩子還是右孩子if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}//刪除delete cur;}//左右孩子都不為空else{//找當前節點右樹的最左節點來替換Node* parent = cur;Node* subright = cur->_right;while (subright->_left){parent = subright;subright = subright->_left;}swap(cur->_key, subright->_key);//判斷這個節點是parent的左孩子還是右孩子  若刪除的是根節點就是右孩子,因此一定要判斷if (parent->_left == subright){parent->_left = subright->_right;}else{parent->_right = subright->_right;}//刪除delete subright;}//找到返回truereturn true;}}//沒找到return false;}bool FindR(const K& key){return _FindR(_root ,key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}//C++11 強制默認構造函數BSTree() = default;~BSTree(){Destroy(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t->_root);return *this;}private:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* NewRoot = new Node(root->_key);NewRoot->_left = Copy(root->_left);NewRoot->_right = Copy(root->_right);return NewRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){cout << "沒找到" <<key<< endl;return false;}//先找節點if (root->_key > key){return _EraseR(root->_left, key);}else if (root->_key < key){return _EraseR(root->_right, key);}else{//三種情況  左孩子空 右孩子空 左右都不空if (root->_left == nullptr){Node* tmp = root;root = root->_right;delete tmp;return true;}else if (root->_right == nullptr){Node* tmp = root;root = root->_left;delete tmp;return true;}else{//左右孩子都不為空  用左孩子的最右節點 或 右孩子的最左節點Node* subleft = root->_left;while (subleft->_right){subleft = subleft->_right;}swap(root->_key, subleft->_key);return _EraseR(root->_left,key);}}}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key > key){return _FindR(root->_left , key);}else if (root->_key < key){return _FindR(root->_right, key);}else{cout << "找到了" << endl;return true;}}//注意 這里要用 *& 傳值,以保證每次遞歸訪問到每一個節點并能夠對節點進行操作bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key){return _InsertR(root->_left, key);}else if(root->_key < key){return _InsertR(root->_right, key);}else{return false;}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;
};

KV模型

#pragma once#include<iostream>using namespace std;namespace kv
{template <class K, class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key , const V& value):_left(nullptr), _right(nullptr), _key(key),_value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = cur;while (cur){parent = cur;if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){//parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key, value);if (parent->_key > key){parent->_left = cur;}else {parent->_right = cur;}return true;}Node* Find(const K& key){if (_root == nullptr)return nullptr;Node* cur = _root;while(cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}return nullptr;}bool Erase(const K& key){//先找節點if (_root == nullptr)return false;Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//左子樹為空if (cur->_left == nullptr){if (cur == _root){_root = _root->_right;}if (cur == parent->_left){parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}delete cur;}//右子樹為空else if (cur->_right == nullptr){if (cur == _root){_root = _root->_left;}if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}delete cur;}//左右都不為空else{Node* parent = cur;//左子樹的最右節點和cur交換Node* subleft = cur->_left;while (subleft->_right){subleft = subleft->_right;}swap(cur->_key, subleft->_key);delete subleft;}}}//沒找到return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << root->_value << " ";_InOrder(root->_right);}Node* _root = nullptr;};
}

二叉搜索樹的性能怎么樣?

在二叉搜索樹中,插入和刪除操作都必須先查找，查找效率代表了二叉搜索樹中各個操作的性能.
對有n個結點的二叉搜索樹，若每個元素查找的概率相等，則二叉搜索樹平均查找長度是結點在二叉搜索樹的深度的函數，即結點越深，則比較次數越多。
但對于同一個關鍵碼集合，如果各關鍵碼插入的次序不同，可能得到不同結構的二叉搜索樹：
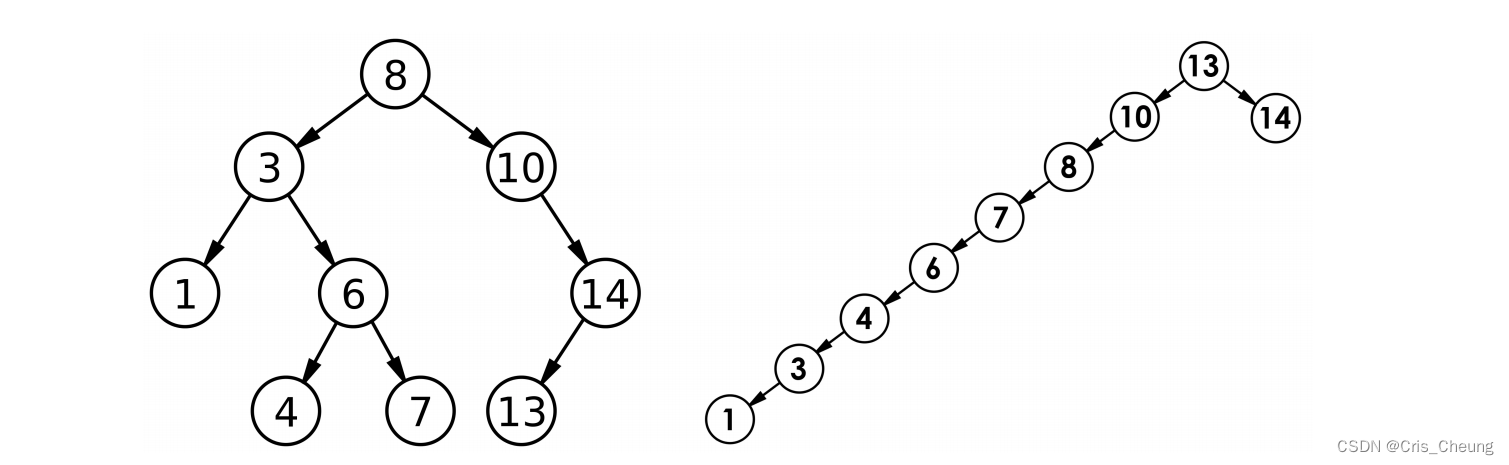
在這里插入圖片描述

最優情況下，二叉搜索樹為完全二叉樹(或者接近完全二叉樹)，其平均比較次數為： l o g 2 N log_2 N log2?N
最差情況下，二叉搜索樹退化為單支樹(或者類似單支)，其平均比較次數為： N 2 \frac{N}{2} 2N?

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/714591.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/714591.shtml
英文地址，請注明出處：http://en.pswp.cn/news/714591.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Linux安裝Nginx詳細步驟

Linux安裝Nginx詳細步驟

1、創建兩臺虛擬機&#xff0c;分別為主機和從機&#xff0c;區別兩臺虛擬機的IP地址 2、將Nginx素材內容上傳到/usr/local目錄&#xff08;pcre,zlib,openssl,nginx&#xff09; 附件 3、安裝pcre庫　　 3.1 cd到/usr/local目錄 3.2 tar -zxvf pcre-8.36.tar.gz 解壓 3.3 cd…
閱讀更多...
MATLAB圖像噪聲添加與濾波

MATLAB圖像噪聲添加與濾波

在 MATLAB 中添加圖像噪聲和進行濾波通常使用以下函數&#xff1a; 添加噪聲&#xff1a;可以使用imnoise函數向圖像添加各種類型的噪聲&#xff0c;如高斯噪聲、椒鹽噪聲等。 濾波&#xff1a;可以使用各種濾波器對圖像進行濾波處理&#xff0c;例如中值濾波、高斯濾波等。 …
閱讀更多...
前端學習、HTML

前端學習、HTML

html是由一些標簽構成的&#xff0c;標簽之間可以嵌套&#xff0c;每個標簽都有開始標簽和結束標簽&#xff0c;也有部分標簽只有開始標簽&#xff0c;沒有結束標簽。html的標簽也可以成為元素。&#xff08;樹形結構&#xff09; html文件的最頂層標簽就是html。 head用來放…
閱讀更多...
**藍橋OJ 178全球變暖 DFS

**藍橋OJ 178全球變暖 DFS

藍橋OJ 178全球變暖 思路: 將每一座島嶼用一個顏色scc代替, 用dx[]和dy[]判斷他的上下左右是否需要標記顏色,如果已經標記過顏色或者是海洋就跳過.后面的淹沒,實際上就是哪個塊上下左右有陸地,那么就不會被淹沒,我用一個tag標記,如果上下左右一旦有海洋,tag就變為false.如果tag…
閱讀更多...
用冒泡排序模擬C語言中的內置快排函數qsort！

用冒泡排序模擬C語言中的內置快排函數qsort！

目錄 ?編輯 1.回調函數的介紹 2. 回調函數實現轉移表 3. 冒泡排序的實現 4. qsort的介紹和使用 5. qsort的模擬實現 6. 完結散花 悟已往之不諫&#xff0c;知來者猶可追 創作不易&#xff0c;寶子們&#xff01;如果這篇文章對你們有幫助的話&#xff0c;別忘了給個免…
閱讀更多...
機器學習：模型評估和模型保存

機器學習：模型評估和模型保存

一、模型評估 from sklearn.metrics import accuracy_score, confusion_matrix, classification_report# 使用測試集進行預測 y_pred model.predict(X_test)# 計算準確率 accuracy accuracy_score(y_test, y_pred) print(f"Accuracy: {accuracy*100:.2f}%")# 打印…
閱讀更多...
整數和浮點數在內存中的存儲（大小端字節序，浮點數的存取）

整數和浮點數在內存中的存儲（大小端字節序，浮點數的存取）

目錄 1.整數在內存中的存儲 2.大小端字節序和字節序判斷 2.1什么是大小端&#xff1f; 2.2為什么會有大小端 3.浮點數在內存中的存儲 3.1浮點數的存儲 3.1.1 浮點數存的過程 3.1.2 浮點數取的過程 3.2 解析 3.3 驗證浮點數的存儲方式 1.整數在內存中的存儲 整數的二進…
閱讀更多...
PAT (Basic Level) Practice | 朋友數

PAT (Basic Level) Practice | 朋友數

如果兩個整數各位數字的和是一樣的&#xff0c;則被稱為是“朋友數”&#xff0c;而那個公共的和就是它們的“朋友證號”。例如 123 和 51 就是朋友數&#xff0c;因為 123 51 6&#xff0c;而 6 就是它們的朋友證號。給定一些整數&#xff0c;要求你統計一下它們中有多少個不…
閱讀更多...
億道信息輕工業三防EM-T195，零售、制造、倉儲一網打盡

億道信息輕工業三防EM-T195，零售、制造、倉儲一網打盡

厚度僅10.5mm&#xff0c;重量僅0.65千克的EM-T195&#xff0c;其緊湊而纖薄的設計為以往加固型平板帶來了全新的輕薄概念。盡管設計時尚、輕薄&#xff0c;但經過軍用認證的強固性仍然能夠承受所有具有挑戰性的環境條件。隨身攜帶無負擔的輕便性加上抗震功能使其成為餐廳、酒店…
閱讀更多...
C++_數據類型_字符型

C++_數據類型_字符型

作用 字符型變量用于顯示單個字符 語法 char ch a;注意 在顯示字符型變量時&#xff0c;用單引號將字符括起來&#xff0c;不要用雙引號單引號只能有一個字符&#xff0c;不可以是字符串 C和C中字符型變量只占用一個字節字符型變量并不是把字符本身放到內存中存儲&#xf…
閱讀更多...
Excel導出

Excel導出

目錄 Maven依賴 實體類 表頭列寬自適應處理器 行列凍結處理器 合并單元格處理器 工具類 Maven依賴 <!--easy excel--><dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.3.2</vers…
閱讀更多...
數獨游戲(dfs)

數獨游戲(dfs)

代碼注釋如下 #include <iostream> using namespace std; const int N 10; bool col[N][N], rol[N][N], cell[3][3][N]; char g[N][N]; bool dfs(int x, int y) { //用bool這樣在找到一個方案就可以迅速退出if(y 9) x, y 0; //若y超出邊界&#xff0c;則第二…
閱讀更多...
S1---FPGA硬件板級原理圖實戰導學

S1---FPGA硬件板級原理圖實戰導學

視頻鏈接 FPGA板級實戰導學01_嗶哩嗶哩_bilibili FPGA硬件板級原理圖實戰導學 【硬件電路設計的方法和技巧-嗶哩嗶哩】硬件電路設計的方法和技巧01_嗶哩嗶哩_bilibili&#xff08;40min&#xff09; 【高速板級硬件電路設計-嗶哩嗶哩】 高速板級硬件電路設計1_嗶哩嗶哩_bil…
閱讀更多...
【RT-Thread基礎教程】郵箱的使用

【RT-Thread基礎教程】郵箱的使用

文章目錄 前言一、郵箱的特性二、郵箱操作函數2.1 創建郵箱創建動態郵箱創建靜態郵箱 2.2 刪除郵箱2.3 發郵件2.4 取郵件 三、示例代碼總結 前言 RT-Thread是一個開源的實時嵌入式操作系統&#xff0c;廣泛應用于各種嵌入式系統和物聯網設備。在RT-Thread中&#xff0c;郵箱是…
閱讀更多...
輸入一個整數，輸出其最長連續因子。

輸入一個整數，輸出其最長連續因子。

輸入一個整數&#xff0c;輸出其最長連續因子。 例如 輸入&#xff1a;60 輸出&#xff1a;2 3 4 5 6 注意&#xff1a;1不算因子 輸入輸出格式 輸入描述: 輸入一個整數N&#xff0c;N<10000。 輸出描述: 輸出其最長連續因子&#xff0c;如果有多個最長&#xff0c;輸出…
閱讀更多...
HTML5浮動

HTML5浮動

1.標準文檔流組成 塊級元素&#xff08;block&#xff09; 內聯元素&#xff08;inline&#xff09; 2.display屬性 作用&#xff1a;指定HTML標簽的顯示方式 常用屬性 值 說明 block 塊級元素的默認值&#xff0c;元素會被顯示為塊級元素&#xff0c;該元素前后會帶有換行…
閱讀更多...
Linux UnixODBC安裝配置

Linux UnixODBC安裝配置

配置 UnixODBC 夢之上關注IP屬地: 香港 0.2322020.12.09 13:23:10字數 1,202閱讀 5,447 麒麟&達夢適配系列: 1.麒麟服務器上安裝 DM8 2.配置 UnixODBC 3.beego-ORM 適配達夢 資源緊張的時候&#xff0c;服務器是大家共用的&#xff0c;上面部署了一堆服務。所以選用doc…
閱讀更多...
Lua速成（7）

Lua速成（7）

一、Lua 元表(Metatable) 在 Lua table 中我們可以訪問對應的 key 來得到 value 值&#xff0c;但是卻無法對兩個 table 進行操作(比如相加)。 因此 Lua 提供了元表(Metatable)&#xff0c;允許我們改變 table 的行為&#xff0c;每個行為關聯了對應的元方法。 例如&#xf…
閱讀更多...
ShardingJdbc實戰-分庫分表

ShardingJdbc實戰-分庫分表

文章目錄 基本配置分庫分表的分片策略一、inline 行表達時分片策略algorithm-expression行表達式完整案例和配置如下 二、根據實時間日期 - 按照標準規則分庫分表標準分片 - Standard完整案例和配置如下 基本配置 邏輯表 邏輯表是指&#xff1a;水平拆分的數據庫或者數據表的相…
閱讀更多...
SpringBoot實戰（1）

SpringBoot實戰（1）

SpringBoot總結 一,Spring 設計思想 OOP: 面向對象編程-》封裝、繼承、多態 BOP: 面向Bean編程-》一切從Bean開始 AOP: 面向切面編程-》解藕、專 人做專事 IOC: 控制反轉,將new 對象的操作交給Spring統一管理-》轉交控制權 DI/DL: 依賴注入/依賴查找-》自動賦值 DI和AOP…
閱讀更多...
最新文章

Copyright @ 2022~2023