?
目錄
1.整數在內存中的存儲
2.大小端字節序和字節序判斷
2.1什么是大小端?
2.2為什么會有大小端
3.浮點數在內存中的存儲
3.1浮點數的存儲
3.1.1 浮點數存的過程
3.1.2 浮點數取的過程
3.2 解析
3.3 驗證浮點數的存儲方式

1.整數在內存中的存儲
整數的二進制表示方法有三種,即原碼、反碼、補碼。
三種表示方法均有符號位和數值位兩部分,數值位的最高位被當作符號位,其中0表示“正”,1表示“負”,剩余的位則為數值位。
對于正整數,它的原碼、反碼、補碼都相同。
對與負整數,則三種表示方法各不相同:
原碼:直接將數值按照正負數的形式翻譯成?進制得到的就是原碼
反碼:將原碼的符號位不變,其他位依次按位取反就可以得到反碼
補碼:反碼+1就得到補碼
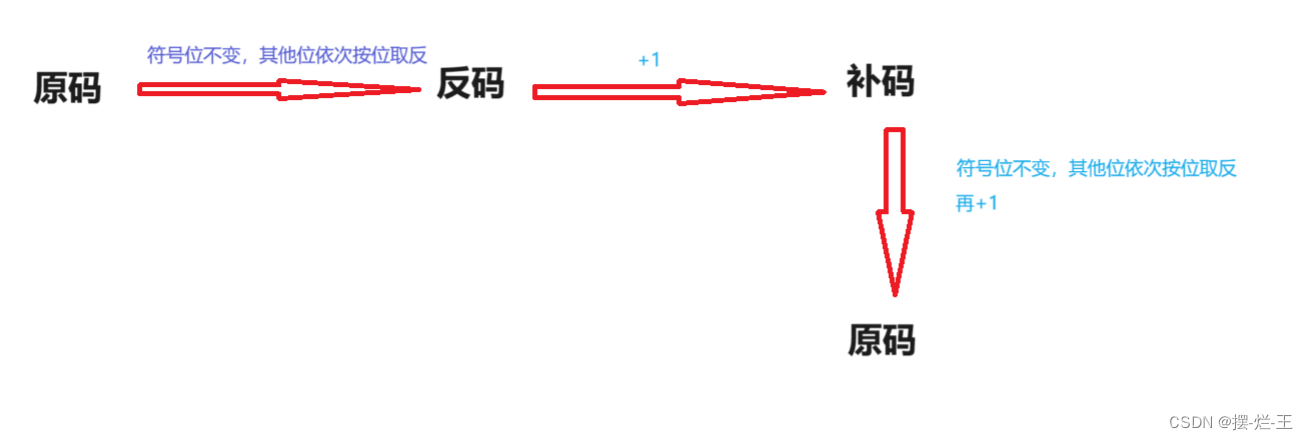
計算機再存儲整數時,存放的都是補碼。
原因是:
1.在計算機系統中,數值?律?補碼來表示和存儲。原因在于,使用補碼,可以將符號位和數值域統一處理;
2.同時,加法和減法也可以統?處理(CPU只有加法器)此外,補碼與原碼相互轉換,其運算過程是相同的,不需要額外的硬件電路。
2.大小端字節序和字節序判斷
下面我們以一段代碼來觀察數據的存儲

通過調試,我們可以發現0x11223344這個數字是以字節為單位,倒著存儲的。
究其原因,我們了解到數據在內存中存儲的順序與大小端有關。
2.1什么是大小端?
大端(存儲)模式:是指數據的低位字節內容保存在內存的高地址處,而數據的高位字節內容,保存 在內存的低地址處。
小端(存儲)模式:是指數據的低位字節內容保存在內存的低地址處,而數據的高位字節內容,保存在內存的高地址處。
上面展示的就是按照小端模式存儲字節順序的。
我們也可以通過一端代碼來判斷我們的硬件是通過哪種模式來存儲字節順序的。
方法一:
#include<stdio.h>
int check()
{int i = 1;return (*(char*)&i);
}
int main()
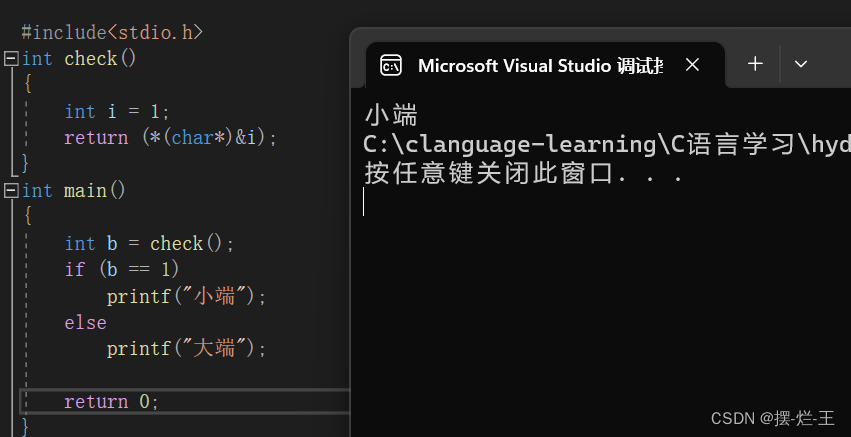
{int b = check();if (b == 1)printf("小端");elseprintf("大端");return 0;
}
方法二:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{union {char a;int b;}u;u.b = 1;if (u.a == 1)printf("小端");elseprintf("大端");return 0;
}2.2為什么會有大小端
在計算機系統中,是以字節為單位的,每個地址單元都 對應著?個字節,?個字節為8bit 位,但是在C語言中除了8 bit 的 char 之外,還有16 bit 的 short 型,32 bit 的 long 型(要看具體的編譯器),另外,對于位數大于8位的處理器,例如16位 或者32位的處理器,由于寄存器寬度大于一個字節,那么必然存在著一個如何將多個字節安排的問題。因此就導致了大端存儲模式和小端存儲模式。
例如:?個16bit 的 short 型 x ,在內存中的地址為 0x0010 , x 的值為 0x1122 ,那么 0x11 為高字節, 0x22 為低字節。對于?端模式,就將 0x11 放在低地址中,即 0x0010 中, 0x22 放在高地址中,即 0x0011 中。小端模式,剛好相反。我們常用的 X86 結構是小端模式,而KEIL C51 則為大端模式。很多的ARM,DSP都為小端模式。有些ARM處理器還可以由硬件來選擇是大端模式還是小端模式。
3.浮點數在內存中的存儲
先看下面一段代碼的輸出結果是什么?
#include<stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值為:%d\n", n);printf("*pFloat的值為:%f\n", *pFloat);*pFloat = 9.0;printf("num的值為:%d\n", n);printf("*pFloat的值為:%f\n", *pFloat);return 0;
}在看到答案之前各位可以思考一下到底會輸出什么?
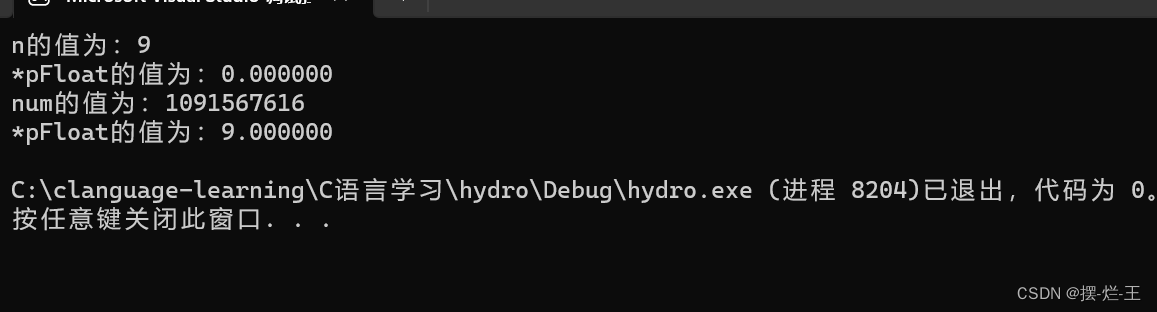
想必看到答案后,各位都應該和我最初看到答案是一樣懵。
對于上面的問題,其實就是關于浮點數在內存中的存儲方式。下面就來講講浮點數在內存中究竟是如何存儲的。
3.1浮點數的存儲
根據國際標準IEEE(電?和電??程協會) 754,任意?個?進制浮點數V可以表示成下面的形式:
? (?1)S 表示符號位,當S=0,V為正數;當S=1,V為負數
? M 表示有效數字,M是大于等于1,小于2的?
? 2 E 表示指數位
?舉例來說:
十進制的5.0,寫成二進制是 101.0 ,相當于 1.01×2^2 。 那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十進制的-5.0,寫成二進制是 -101.0 ,相當于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754規定:
對于32位的浮點數,最高的1位存儲符號位S,接著的8位存儲指數E,剩下的23位存儲有效數字M
 對于64位的浮點數,最高的1位存儲符號位S,接著的11位存儲指數E,剩下的52位存儲有效數字M
對于64位的浮點數,最高的1位存儲符號位S,接著的11位存儲指數E,剩下的52位存儲有效數字M
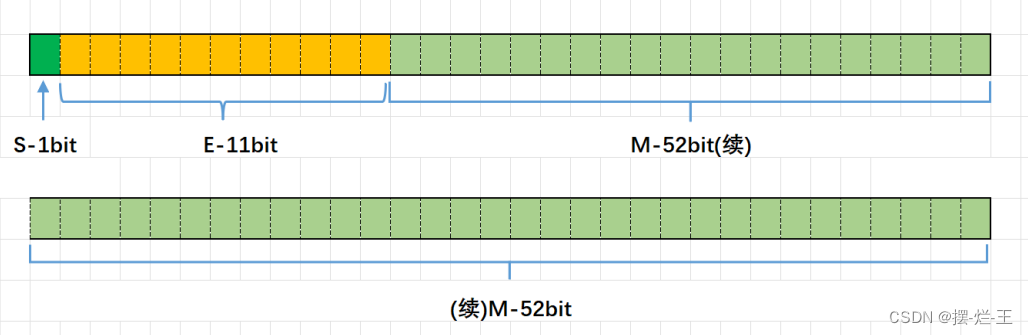
3.1.1 浮點數存的過程
IEEE 754對有效數字M和指數E,還有?些特別規定。
前面說過, 1≤M<2 ,也就是說,M可以寫成 1.xxxxxx 的形式,其中xxxxxx表示小數部分。 IEEE 754規定,在計算機內部保存M時,默認這個數的第?位總是1,因此可以被舍去,只保存后?的 xxxxxx部分。比如保存1.01的時候,只保存01,等到讀取的時候,再把第?位的1加上去。這樣做的目的,是節省1位有效數字。以32位浮點數為例,留給M只有23位,將第?位的1舍去以后,等于可以保存24位有效數字。
對于指數E,它是一個無符號整數。
如果E為8為,則它的取值范圍是0~255;如果E為16位,則它的取值范圍位0~2047。但是,在科學計數法中是可以出現負數的,所以IEEE 754規定,,存?內存時E的真實值必須再加上 ?個中間數,對于8位的E,這個中間數是127;對于11位的E,這個中間數是1023。比如,2^10的E是 10,所以保存成32位浮點數時,必須保存成10+127=137,即10001001。
3.1.2 浮點數取的過程
指數E從內存中取出可以分為三種情況:
E不全為0或不全為1
指數E的計算值減去127(或1023),得到真實值,再將有效數字前加上1。
例如,0.5的二進制形式0.1,由于規定整數部分必須為1,所以小數點向右移動一位,則為1.0*2^(-1),其 階碼為-1+127(中間值)=126,表?為01111110,?尾數1.0去掉整數部分為0,補?0到23位,其二進制表示為
0 01111110 00000000000000000000000
E全為0
這時,浮點數的指數E等于1-127(或者1-1023)即為真實值,有效數字M不再加上第?位的1,而是還 原為0.xxxxxx的小數。這樣做是為了表示±0,以及接近于0的很小的數字。
E全為1
這時,如果有效數字M全為0,表示±無窮大(正負取決于符號位s);
3.2 解析
回到之前提到的題目,為什么 9 還原成浮點數,就成了 0.000000 ?
首先看9是如何存儲在內存中的
0000 0000 0000 0000 0000 0000 0000 1001
然后,將 9 的?進制序列按照浮點數的形式拆分,得到第一位符號位s=0,后面8位的指數 E=00000000 , 最后23位的有效數字M=000 0000 0000 0000 0000 1001。
由于指數E全為0,所以符合E為全0的情況。因此,浮點數V就寫成:
V=(-1)^0 × 0.00000000000000000001001×2^(-126)=1.001×2^(-146)
顯然,V是?個很?的接近于0的正數,所以??進制?數表?就是0.000000。
至于浮點數9.0,為什么整數打印是 1091567616?
首先,浮點數9.0等于二進制1001.0,換算成科學計數法是:1.001×2^3。
所以: 9.0? = ?(?1) ? ? 0 ?(1.001)? ? ?23 ,
最后寫成二進制形式就是
0 10000010 001 0000 0000 0000 0000 0000
這個32位的?進制數,被當做整數來解析的時候,就是整數在內存中的補碼,原碼正是 1091567616 。
3.3 驗證浮點數的存儲方式
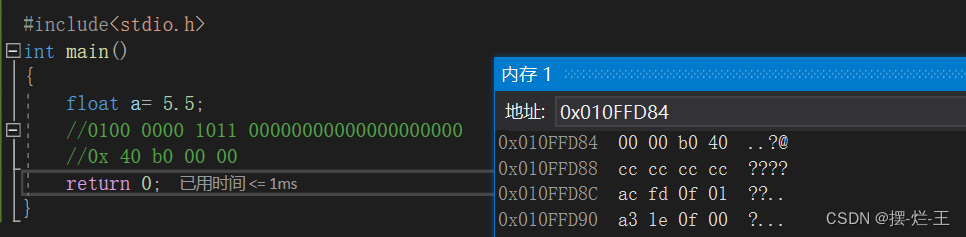
以5.5為例,它的二進制表示為101.1,即1.011*2^2,則S=0,M=1.011,E=2+127=129,
最后寫成二進制形式就是
0 10000001 01100000000000000000000
?
____________________
?感謝你的閱讀,希望本文能夠對你有所幫助。如果你喜歡我的內容,記得點贊關注收藏我的博客,我會繼續分享更多的內容。?
 Practice | 朋友數)



)





)

)

)


)

版本庫 —— 存儲系統,存儲目錄,提交對象及其命名、移動與復制~)