引言

這幾天一直在做二分的題，都是上了難度的題目，本來以為自己的二分水平已經非常熟悉了，沒想到還是糊涂了一兩天才重新想清楚，想明白，還是得繼續不斷地刷題，把這些類型的題刷明白，刷透了，就可以了，加油！

概念

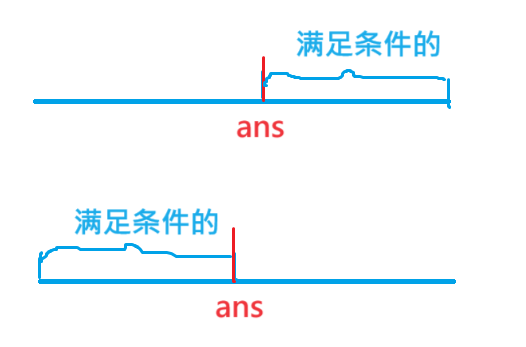
一般只有這兩種情況，具體模板可以參考之前的博客二分，再特殊一點的就是本篇博客的第五、六題了，但看我的解析，都是一樣的步驟。

---

一、借教室

標簽：二分

思路：這道題如果用暴力來做的話就是遍歷 $m$ 個訂單，每個訂單然后去判斷是否正確，去判斷沒天中的訂單是否滿足要求，就這樣也是 $10^{12}$ 明顯超時了。可以用二分來做，因為這個訂單是具有單調性的，假設第 $k$ 個訂單是第一個不滿足要求的，那么之后的訂單也是不滿足要求的，判斷依據就是定義一個天數數組 $b[i]$ ，每天的訂單數是不能超過 $w[i]$ 的，所以可以用二分檢查條件從而判斷出第一個不滿足的，然后再 $s_j～t_j$天要用 $d_j$個教室可以用差分來做，這樣就可以了。
這相當于一個模型：有多個訂單，每天進行多個操作，問訂單會不會滿足條件.

題目描述：

在大學期間，經常需要租借教室。大到院系舉辦活動，小到學習小組自習討論，都需要向學校申請借教室。教室的大小功能不同，借教室人的身份不同，借教室的手續也不一樣。?面對海量租借教室的信息，我們自然希望編程解決這個問題。我們需要處理接下來 n 天的借教室信息，其中第 i 天學校有 ri 個教室可供租借。共有 m 份訂單，每份訂單用三個正整數描述，分別為 dj,sj,tj，表示某租借者需要從第 sj 天到第 tj 天租借教室（包括第 sj天和第 tj 天），每天需要租借 dj 個教室。?我們假定，租借者對教室的大小、地點沒有要求。即對于每份訂單，我們只需要每天提供 dj 個教室，而它們具體是哪些教室，每天是否是相同的教室則不用考慮。?借教室的原則是先到先得，也就是說我們要按照訂單的先后順序依次為每份訂單分配教室。如果在分配的過程中遇到一份訂單無法完全滿足，則需要停止教室的分配，通知當前申請人修改訂單。這里的無法滿足指從第 sj 天到第 tj 天中有至少一天剩余的教室數量不足 dj 個。?現在我們需要知道，是否會有訂單無法完全滿足。如果有，需要通知哪一個申請人修改訂單。輸入格式
第一行包含兩個正整數 n,m，表示天數和訂單的數量。?
第二行包含 n 個正整數，其中第 i 個數為 ri，表示第 i 天可用于租借的教室數量。?
接下來有 m 行，每行包含三個正整數 dj,sj,tj，表示租借的數量，租借開始、結束分別在第幾天。?
每行相鄰的兩個數之間均用一個空格隔開。
天數與訂單均用從 1 開始的整數編號。輸出格式
如果所有訂單均可滿足，則輸出只有一行，包含一個整數 0。
否則（訂單無法完全滿足）輸出兩行，第一行輸出一個負整數 ?1，第二行輸出需要修改訂單的申請人編號。數據范圍
1≤n,m≤106,0≤ri,dj≤109,1≤sj≤tj≤n
輸入樣例：
4 3
2 5 4 3
2 1 3
3 2 4
4 2 4
輸出樣例：
-1
2

示例代碼：

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e6+10;int n, m;
int w[N];
int d[N], s[N], t[N];
LL b[N];bool check(int mid)
{memset(b, 0, sizeof b);for(int i = 1; i <= mid; ++i){b[s[i]] += d[i];b[t[i]+1] -= d[i];}for(int i = 1; i <= n; ++i){b[i] += b[i-1];if(b[i] > w[i]) return true;}return false;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i) cin >> w[i];for(int i = 1; i <= m; ++i) cin >> d[i] >> s[i] >> t[i];int l = 1, r = m;while(l < r){int mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}if(check(r)){cout << -1 << endl;cout << r << endl;}else{cout << 0 << endl;}return 0;
}

---

二、分巧克力

標簽：二分

思路：這道題首先滿足單調性，分的巧克力的大小在一定值后就不能切除 $K$ 塊巧克力了，所以可以用二分來求答案。

題目描述：

兒童節那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友們。小明一共有 N 塊巧克力，其中第 i 塊是 Hi×Wi 的方格組成的長方形。為了公平起見，小明需要從這 N 塊巧克力中切出 K 塊巧克力分給小朋友們。切出的巧克力需要滿足：形狀是正方形，邊長是整數大小相同例如一塊 6×5 的巧克力可以切出 6 塊 2×2 的巧克力或者 2 塊 3×3 的巧克力。當然小朋友們都希望得到的巧克力盡可能大，你能幫小明計算出最大的邊長是多少么？輸入格式
第一行包含兩個整數 N 和 K。
以下 N 行每行包含兩個整數 Hi 和 Wi。
輸入保證每位小朋友至少能獲得一塊 1×1 的巧克力。輸出格式
輸出切出的正方形巧克力最大可能的邊長。數據范圍
1≤N,K≤105,1≤Hi,Wi≤105
輸入樣例：
2 10
6 5
5 6
輸出樣例：
2

示例代碼：

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10;int n, k;
int h[N], w[N];bool check(int mid)
{LL s = 0;for(int i = 1; i <= n; ++i){s += ((LL)h[i] / mid) * (w[i] / mid);if(s >= k) return true;}return false;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> k;for(int i = 1; i <= n; ++i) cin >> h[i] >> w[i];int l = 1, r = 1e5;while(l < r){int mid = l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << r << endl;return 0;
}

---

三、管道

標簽：二分

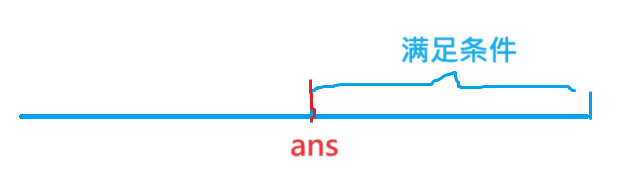
思路：這道題一看是求最早的時間，根據題意可以知道時間到了一定的值，那么后面的時間都可以滿足條件，那么可以利用二分來枚舉時間，然后根據判斷條件來找到滿足條件的第一個點。然后判斷條件可以通過時間來算出來每個閥門在當前時間能夠經過的區間，然后把這些區間合并，如果最后的區間包含了所有的區間那么就是滿足條件的。而且這個區間可以是不重疊也可以合并的，因為 $[1,2]$ 和 $[3,4]$ 都能覆蓋到，那么說明 $[1,4]$ 都能檢測道水流。

題目描述：

有一根長度為 len 的橫向的管道，該管道按照單位長度分為 len 段，每一段的中央有一個可開關的閥門和一個檢測水流的傳感器。一開始管道是空的，位于 Li 的閥門會在 Si 時刻打開，并不斷讓水流入管道。對于位于 Li 的閥門，它流入的水在 Ti（Ti≥Si）時刻會使得從第 Li?(Ti?Si) 段到第 Li+(Ti?Si) 段的傳感器檢測到水流。求管道中每一段中間的傳感器都檢測到有水流的最早時間。輸入格式
輸入的第一行包含兩個整數 n,len，用一個空格分隔，分別表示會打開的閥門數和管道長度。接下來 n 行每行包含兩個整數 Li,Si，用一個空格分隔，表示位于第 Li 段管道中央的閥門會在 Si 時刻打開。輸出格式
輸出一行包含一個整數表示答案。數據范圍
對于 30% 的評測用例，n≤200，Si,len≤3000；
對于 70% 的評測用例，n≤5000，Si,len≤105；
對于所有評測用例，1≤n≤105，1≤Si,len≤109，1≤Li≤len，Li?1<Li。輸入樣例：
3 10
1 1
6 5
10 2
輸出樣例：
5

示例代碼：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;const int N = 1e5+10;int n, len;
int L[N], S[N];
PII segs[N];bool check(int mid)
{int cnt = 0;for(int i = 1; i <= n; ++i){if(mid >= S[i]){int t = mid - S[i];int l = max(1, L[i] - t), r = min((LL)len, (LL)L[i] + t);segs[cnt++] = {l,r};}}sort(segs, segs+cnt);int l = -2e9, r = -2e9;for(int i = 0; i < cnt; ++i){if(segs[i].first > r + 1) l = segs[i].first, r = segs[i].second;else r = max(r, segs[i].second);}return l == 1 && r == len;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> len;for(int i = 1; i <= n; ++i) cin >> L[i] >> S[i];int l = 0, r = 2e9;  // 等到1e9開閥門，再經過1e9從左邊流到右邊while(l < r){int mid = (LL)l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << r << endl;return 0;
}

---

四、技能升級

標簽：二分

思路1：首先這道題先用了堆來做，過了7/12個數據，代碼隨后附上。
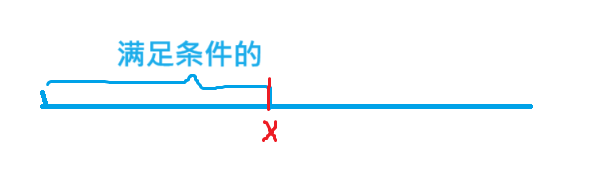
思路2：做題首先要先到怎么做出來然后再想時間復雜度的問題，首先這道題肯定是把所有的數加起來，然后從大到小排序選前 $M$ 個數，就是最大的，那么實際上也是從這里面選前 $M$ 個最大的數。那么我們假設第 $M$ 個數為 $x$ ，那么一定滿足大于等于 $x$ 的個數一定是大于等于 $M$ 的，并且大于等于 $x+1$的個數一定是小于 $M$ 個的，因為x越大值就越少，越小值就越多，然后可以求出來 $x$ ，然后最后的結果和個數可以通過數學公式來推出來，最后還要統計個數如果超 $M$ 個了，這是因為可能有跟 $x$ 一樣的數，所以減去多余的即可。
模型：多路歸并算法

題目描述：

小藍最近正在玩一款 RPG 游戲。他的角色一共有 N 個可以加攻擊力的技能。其中第 i 個技能首次升級可以提升 Ai 點攻擊力，以后每次升級增加的點數都會減少 Bi。?AiBi?（上取整）次之后，再升級該技能將不會改變攻擊力。現在小藍可以總計升級 M 次技能，他可以任意選擇升級的技能和次數。請你計算小藍最多可以提高多少點攻擊力？輸入格式
輸入第一行包含兩個整數 N 和 M。
以下 N 行每行包含兩個整數 Ai 和 Bi。輸出格式
輸出一行包含一個整數表示答案。數據范圍
對于 40% 的評測用例，1≤N,M≤1000；
對于 60% 的評測用例，1≤N≤104，1≤M≤107；
對于所有評測用例，1≤N≤105，1≤M≤2×109，1≤Ai,Bi≤106。輸入樣例：
3 6
10 5
9 2
8 1
輸出樣例：
47

在這里插入代碼片

示例代碼一： 堆 7/12

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10;int n, m;
int a[N], b[N];
priority_queue<PII> heap;int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i) {cin >> a[i] >> b[i];heap.push({a[i], b[i]});}LL res = 0;while(m-- && heap.size()){auto t = heap.top(); heap.pop();res += t.x;if(t.x - t.y <= 0) continue;  //為0的就不加進去了，加了最大值也不變還會增加時間復雜度heap.push({t.x-t.y, t.y});}cout << res << endl;return 0;
}

示例代碼二： 二分 12/12

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10;int n, m;
int a[N], b[N];bool check(int mid)
{LL s = 0;for(int i = 1; i <= n; ++i){if(a[i] >= mid){s += (a[i] - mid) / b[i] + 1;if(s >= m) return true;}}return false;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i) cin >> a[i] >> b[i];int l = 0, r = 1e6;  // l可能取0，即全部包含進去while(l < r){int mid = l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}LL res = 0, cnt = 0;for(int i = 1; i <= n; ++i){if(a[i] >= r){int c = (a[i] - r) / b[i] + 1;int end = a[i] - (c - 1) * b[i];cnt += c;res += (LL)(a[i] + end) * c / 2;}}cout << res - (cnt - m) * r << endl;return 0;
}

---

五、冶煉金屬

標簽：二分

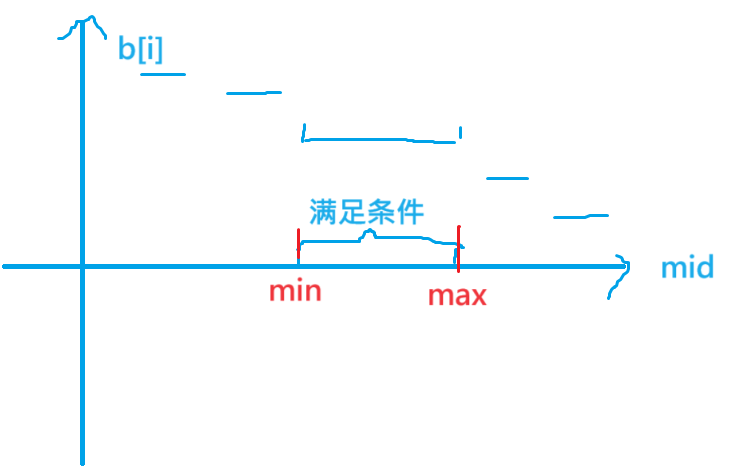
思路：這道題其實就是如下圖所示的一種二分，在滿足條件的情況下，找到 $mid$ 的最小值和最大值，然后就是一些細節問題，我標在注釋里了。

題目描述：

小藍有一個神奇的爐子用于將普通金屬 O 冶煉成為一種特殊金屬 X。這個爐子有一個稱作轉換率的屬性 V，V 是一個正整數，這意味著消耗 V 個普通金屬 O 恰好可以冶煉出一個特殊金屬 X
，當
普通金屬 O 的數目不足 V 時，無法繼續冶煉。現在給出了 N 條冶煉記錄，每條記錄中包含兩個整數 A 和 B，這表示本次投入了 A 個普通金屬 O，最終冶煉出了 B 個特殊
金屬 X。每條記錄都是獨立的，這意味著上一次沒消耗完的普通金屬 O 不會累加到下一次的冶煉當中。根據這 N 條冶煉記錄，請你推測出轉換率 V 的最小值和最大值分別可能是多少，題目保證評測數據不存在無解的情況。輸入格式
第一行一個整數 N，表示冶煉記錄的數目。
接下來輸入 N 行，每行兩個整數 A、B，含義如題目所述。輸出格式
輸出兩個整數，分別表示 V 可能的最小值和最大值，中間用空格分開。數據范圍
對于 30% 的評測用例，1≤N≤102。
對于 60% 的評測用例，1≤N≤103。
對于 100% 的評測用例，1≤N≤104，1≤B≤A≤109。輸入樣例：
3
75 3
53 2
59 2
輸出樣例：
20 25
樣例解釋
當 V=20 時，有：?7520?=3，?5320?=2，?5920?=2，可以看到符合所有冶煉記錄。
當 V=25 時，有：?7525?=3，?5325?=2，?5925?=2，可以看到符合所有冶煉記錄。
且再也找不到比 20 更小或者比 25 更大的符合條件的 V 值了。

示例代碼：

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e4+10;int n;
int a[N], b[N];bool check1(int mid)  // 這里的check判斷的為是否在右半邊
{for(int i = 1; i <= n; ++i){  // 說明在左半邊if(a[i] / mid > b[i]) return false;  // 最小值，滿足條件的是右半邊，mid越大值越小，所以當大于b[i]時就不滿足條件了}return true;
}bool check2(int mid)
{for(int i = 1; i <= n; ++i){if(a[i] / mid < b[i]) return false;  // 同理，當小于b[i]時說明在右半邊，而二分的正確的條件應該是左半邊}return true;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> a[i] >> b[i];int r1, r2;int l = 1, r = 1e9;  // 因為a[i], b[i]的值可能為1e9,1while(l < r){  // 注意這里其實暴不了int因為就是是兩個1e9也沒用int mid = (LL)l + r >> 1;  // 這里的check判斷的為是否在右半邊if(check1(mid)) r = mid;  // 找最小值，發現右邊是條件一樣的，所以 r = midelse l = mid + 1;}r1 = r;l = 1, r = 1e9;while(l < r){int mid = (LL)l + r + 1 >> 1;if(check2(mid)) l = mid;  // 找最大值，發現左邊和自己的條件是一樣的，所以l = midelse r = mid - 1;}r2 = r;cout << r1 << " " << r2 << endl;return 0;
}

---

六、數的范圍

標簽：二分

思路：這道題真的寫了非常多遍了，但寫的時候還是出錯，而且還把我搞迷糊了一兩天，導致其他的二分題都不會了，都不知道怎么做了，好在自己堅持，慢慢耗、磨出來了，知道了 $check$ 函數和區間判斷怎么寫了，思路一下子清晰了，然后其余的二分題用這個方法也正確的做出來了。首先你要有個條件，比如說這道題是 $a[mid]=x$，然后找滿足這個條件的 $mid$ 的最小值和最大值 ，然后比如說你要找 $r1$，那么和 $r1$ 滿足相同條件的在 $r1$ 的右半邊，所以 $check$ 函數為 $mid$ 在右半部分滿足什么條件，即 $a[mid]\ge x$ ，然后因為滿足條件的在右半部分所以這個條件下的語句為 $r=mid$ ，然后 $l=mid+1$ ，這個 $r=mid,l=mid+1$和 $l=mid,r=mid?1$都是一一對應的， $check$ 條件下寫前面的， $else$ 下寫后面的，然后如果是 $l=mid$ 語句，那么在 $intmid=l+r>>1$那，要改成 $intmid=l+r+1>>1$，否則會有邊界問題。然后說一下最大值，再梳理一遍，其最大值，滿足相同條件的在左部分，雖然只有一部分但只要這么想就是對的， $check$ 為 $a[mid]\le x$ ，因為在滿足條件的在左邊所以 $l=mid$ ，然后就是 $r=mid?1$ ，再在二分 $mid$ 那加一。

題目描述：

給定一個按照升序排列的長度為 n 的整數數組，以及 q 個查詢。對于每個查詢，返回一個元素 k 的起始位置和終止位置（位置從 0 開始計數）。如果數組中不存在該元素，則返回 -1 -1。輸入格式
第一行包含整數 n 和 q，表示數組長度和詢問個數。
第二行包含 n 個整數（均在 1～10000 范圍內），表示完整數組。
接下來 q 行，每行包含一個整數 k，表示一個詢問元素。輸出格式
共 q 行，每行包含兩個整數，表示所求元素的起始位置和終止位置。如果數組中不存在該元素，則返回 -1 -1。數據范圍
1≤n≤100000
1≤q≤10000
1≤k≤10000
輸入樣例：
6 3
1 2 2 3 3 4
3
4
5
輸出樣例：
3 4
5 5
-1 -1

示例代碼：

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10;int n, q;
int a[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> q;for(int i = 0; i < n; ++i) cin >> a[i];while(q--){int x;cin >> x;int r1 = -1, r2 = -1;int l = 0, r = n - 1;  // 注意看好起始位置從幾開始的while(l < r){int mid = (LL)l + r >> 1;if(a[mid] >= x) r = mid;  // 先看點，然后看相同條件的區間在哪來判斷check，然后區間在右就是r = midelse l = mid + 1;         // 在左就是l = mid，其余的else和+1跟著變就行}if(a[r] == x) r1 = r;l = 0, r = n - 1;while(l < r){int mid = (LL)l + r + 1 >> 1;if(a[mid] <= x) l = mid;else r = mid - 1;}if(a[r] == x) r2 = r;cout << r1 << " "  << r2 << endl;}return 0;
}

---

七、最佳牛圍欄

標簽：二分、前綴和

思路1：首先這道題用了雙指針跟前綴和，再加上一些限制條件最大化的縮減時間，然后過了 $10/15$ 個數據，還可以。
思路2：首先這道題想著求最大平均值，一般這個求最大最小的這種邊界問題都可以想著用二分來做。首先是否有單調性，如果假設最大平均值為 $mid$ ，那么小于 $mid$ 的肯定有，大于 $mid$ 的肯定沒有，所以可以通過 $check$ 是否存在 $mid$ 來二分出來最大的 $mid$ 。條件就是是否存在一個長度大于等于 $F$ 的連續子區間，使得這個區間的平均值為 $mid$ ，如果給每個點都減去 $mid$ ，那么問題就等于是否存在一個長度大于等于 $F$ 的連續子區間使得這個區間的和非負，那么就可以用前綴和來求，即 $s[j]?s[i]\ge 0$，即 $s[j]\ge s[i]$，既然要找存在，那么這個 $s[i]$ 當然越小越好了，就是找 $i$ 之前的最小的 $s[i]$ ，然后用雙指針算法求，再處理好邊界問題就行了。
模型：從一段區間中找數量大于等于F的連續子區間的最大平均值

題目描述：

農夫約翰的農場由 N 塊田地組成，每塊地里都有一定數量的牛，其數量不會少于 1 頭，也不會超過 2000 頭。約翰希望用圍欄將一部分連續的田地圍起來，并使得圍起來的區域內每塊地包含的牛的數量的平均值達到最大。圍起區域內至少需要包含 F 塊地，其中 F 會在輸入中給出。在給定條件下，計算圍起區域內每塊地包含的牛的數量的平均值可能的最大值是多少。輸入格式
第一行輸入整數 N 和 F，數據間用空格隔開。
接下來 N 行，每行輸入一個整數，第 i+1 行輸入的整數代表第 i 片區域內包含的牛的數目。輸出格式
輸出一個整數，表示平均值的最大值乘以 1000 再 向下取整 之后得到的結果。數據范圍
1≤N≤100000
1≤F≤N
輸入樣例：
10 6
6 
4
2
10
3
8
5
9
4
1
輸出樣例：
6500

示例代碼一： 雙指針、前綴和 10/15

#include <bits/stdc++.h>using namespace std;const int N = 1e5+10;int n, f;
int a[N], s[N];int main()
{cin >> n >> f;for(int i = 1; i <= n; ++i) {cin >> a[i];s[i] = s[i-1] + a[i];}int res = -2e9;for(int i = 1; n - i + 1 >= f; ++i){for(int j = i + f - 1; j <= n; ++j){res = max((double)res, (double)(s[j] - s[i-1]) / (j - i + 1) * 1000);}}cout << res << endl;return 0;
}

示例代碼二：二分、前綴和 15/15

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10;int n, m;
int cow[N];
double sum[N];bool check(double ave)
{for(int i = 1; i <= n; ++i) sum[i] = sum[i-1] + cow[i] - ave;double minv = 0;for(int i = 0, j = m; j <= n; ++i, ++j){minv = min(minv, sum[i]);if(sum[j] >= minv) return true;}return false;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i) cin >> cow[i];double l = 0, r = 2000;while(r - l > 1e-5){double mid = (l + r) / 2;if(check(mid)) l = mid;else r = mid;}cout << (int)(r * 1000) << endl;return 0;
}