第二節數學知識補充

一、線性代數

向量的 $L_2$ 范數（Euclidean范數/Frobenius范數）&矩陣的元素形式范數
- 向量的 $L_2$ 范數： $||x||_2=(|x_1|^2+\cdots+|x_m|^2)^{\frac12}$
- 矩陣的元素形式范數：將 $m\times n$ 矩陣按照列堆棧的形式排列成 $mn \times 1$ 的向量，然后采用向量范數的定義，即可得到矩陣的范數： $||x||_p=\left(\sum_{i=1}^m\sum_{j=1}^n|a_{ij}|^p\right)^{\frac1p}$
  - 其中Frobenius范數（p=2）為： $||A||_F=\left(\sum_{i=1}^m\sum_{j=1}^n|a_{ij}|^2\right)^{\frac12}$ ，也可以寫成跡函數的形式： $||A||_F=<A,A>^{\frac12}=\sqrt{tr(A^HA)}$ 。也可稱為Euclidean范數、Schur范數、Hilbert-Schmidt范數或者L2范數。
兩個矩陣按元素的乘法稱為“哈達瑪積”（Hadamard product）數學符號為 $\odot$ 。在Pytorch中，兩個形狀相同的張量按元素相乘表示為：A*B
兩個向量的點積表示為：torch.dot(x, y)，結果為tensor類型
矩陣向量積 $A x$ 表示為：torch.mv(A, x)，mv=matrix vector multiplication
矩陣和矩陣的乘積表示為：torch.mm(A, B)
向量的 $L_1$ 范數（元素的絕對值之和）表示為：torch.abs(x).sum()
向量的 $L_2$ 范數表示為：torch.norm(x)，結果為tensor類型。注意?需要將tensor的元素類型轉換為float類型，x=x.float()
矩陣的 $F$ 范數（弗羅貝尼烏斯范數）表示為：torch.norm(A)

二、矩陣運算（矩陣求導）

當y是標量，x是列向量時， $\frac{\partial y}{\partial \boldsymbol{x}}$ 是行向量， $\frac{\partial y}{\partial \boldsymbol{x}}=\left[ \frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},...,\frac{\partial y}{\partial x_n} \right]$ 。梯度和等高線正交，指向該點處。值變換最大的方向。
當y是列向量，x是標量時， $\frac{\partial \boldsymbol{y}}{\partial x}$ 是列向量， $\frac{\partial\mathbf{y}}{\partial x}=\begin{bmatrix}\frac{\partial y_1}{\partial x}\\\frac{\partial y_2}{\partial x}\\\vdots\\\frac{\partial y_m}{\partial x}\end{bmatrix}$ 。
當y是列向量，x是列向量時， $\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}$ 是矩陣， $\frac{\partial\mathbf{y}}{\partial\mathbf{x}}=\begin{bmatrix}\frac{\partial\mathbf{y}_1}{\partial\mathbf{x}}\\\frac{\partial\mathbf{y}_2}{\partial\mathbf{x}}\\\vdots\\\frac{\partial\mathbf{y}_m}{\partial\mathbf{x}}\end{bmatrix}=\begin{bmatrix}\frac{\partial\mathbf{y}_1}{\partial x_1},\frac{\partial\mathbf{y}_1}{\partial x_2},\ldots,\frac{\partial\mathbf{y}_1}{\partial x_n}\\\frac{\partial\mathbf{y}_2}{\partial x_1},\frac{\partial\mathbf{y}_2}{\partial x_2},\ldots,\frac{\partial\mathbf{y}_2}{\partial x_n}\\\vdots\\\frac{\partial\mathbf{y}_m}{\partial x_1},\frac{\partial\mathbf{y}_m}{\partial x_2},\ldots,\frac{\partial\mathbf{y}_m}{\partial x_n}\end{bmatrix}$ 。
- $\frac{\partial \left( A\boldsymbol{x} \right)}{\partial \boldsymbol{x}}=A$
- $\frac{\partial \left( \boldsymbol{x}^TA \right)}{\partial \boldsymbol{x}}=A^T$ → $\frac{\partial \left< \boldsymbol{x,w} \right>}{\partial \boldsymbol{w}}=\boldsymbol{x}^T$ ，注意分子求內積運算，x和w都是列向量，求內積時表示為 $\boldsymbol{x}^T \boldsymbol{w}$ 。

三、自動求導

標量的鏈式法則同樣可以擴展到向量，注意形狀。

鏈式求導簡單舉例：
在這里插入圖片描述

Ⅰ自動求導

（1）相關概念

自動求導指計算一個函數在指定值上的導數。有別于符號求導和數值求導。

符號求導（Symbolic Differentiation）：符號求導是基于數學規則（如鏈式法則、冪規則、導數的乘積規則等）進行的求導過程，它能產生導數的精確解析表達式。例如，使用符號計算軟件如 MATLAB 的 Symbolic Math Toolbox 或 Mathematica，用戶可以輸入一個數學函數并得到它的精確導數公式。這種方法的優點是可以提供清晰的數學表達式，有助于深入理解函數行為和優化算法的設計，但它對函數形式有一定要求，不適合處理復雜的非結構化或動態變化的函數。
數值求導（Numerical Differentiation）：數值求導是一種近似求導的方法，它不尋找導數的封閉形式表達式，而是通過對函數在相鄰點的值進行差分來估計導數。例如，使用有限差分方法（如前向差分、后向差分或中心差分）來計算某一點處的導數值。這種方法適用性廣泛，能夠處理任意可計算的函數，但求得的是導數的近似值，且誤差與步長的選擇有關，過大的步長可能導致較大的誤差，過小的步長則可能受到浮點計算精度的影響。

給任何f(x)，不需要知道形式，可以通過數值去擬合導數： $\frac{\partial f(x)}{\partial x}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$
自動求導（Automatic Differentiation，AD）：自動求導是一種結合了符號和數值求導特點的技術，它基于鏈式法則和逆向傳播的思想，追蹤并累加每個計算步驟的微小導數貢獻。在現代機器學習和深度學習框架（如 TensorFlow、PyTorch、Theano 等）中廣泛應用。自動求導分為前向模式（Forward Mode）和反向模式（Reverse Mode，又稱 Backpropagation），其中反向模式尤為適合大型神經網絡中梯度的高效計算。自動求導既能給出精確的導數值，又能處理復雜的、非結構化的函數甚至是包含循環和條件語句的程序，而且相比于純符號求導，它更適合于動態生成的計算圖或大規模優化問題。

（2）計算圖

等價于用鏈式法則的計算過程。計算圖（Computation Graph）是一種用于表示數學運算和變量之間依賴關系的數據結構，將計算表示成了一個無環圖，特別在機器學習和深度學習領域應用廣泛。它通過節點（nodes）和邊（edges）構建，其中節點代表數學運算或者變量值，邊則代表這些運算或變量之間的數據流動路徑，以及它們相互間的依賴關系。

在計算圖中：
- 節點（Operations / Functions）：每個節點執行特定的數學運算，比如加法、乘法、激活函數（如sigmoid、ReLU）、矩陣運算，或者是更復雜的層操作如卷積層或全連接層等。節點沒有具體的數值，直到給定所有輸入值時才會進行計算。
- 邊（Edges / Tensors）：邊連接著不同的節點，代表了數據從一個運算傳遞到另一個運算的過程。邊攜帶的是參與運算的數據，通常表現為多維數組（即張量）。在機器學習中，這些張量通常是權重、偏置、輸入特征或是中間層的輸出。
- 變量（Variables）：計算圖中的變量是具有持久狀態的節點，它們存儲了模型參數或需要在整個訓練過程中更新的中間結果。
- 反向傳播（Backpropagation）：當計算圖用于訓練神經網絡時，反向傳播利用自動求導技術來高效地計算整個圖中所有參數的梯度，這使得我們可以更新網絡權重以最小化損失函數。
計算圖的構造有兩種主要方式：顯式構造（Explicit Construction）和隱式構造（Implicit Construction）。

（1）顯式構造（Explicit Construction）Tensorflow/Theano/MXNet

在顯式構造的計算圖中，程序員明確地定義了計算圖的結構，也就是預先確定了哪些操作（operations）將被執行以及它們之間的依賴關系。程序員通常需要手動構建圖的節點和邊，所有的計算都被組織成一個固定結構的圖，只有在圖構建完成后才能執行計算。

例如，在TensorFlow 1.x版本中，用戶需要通過 tf.Session() 和 tf.Graph() 明確地創建計算圖，并通過 tf.Variable() 和 tf.Operation() 等API來顯式地添加節點。執行時，數據通過計算圖從輸入流向輸出，而梯度計算（如反向傳播）則沿著相反的方向進行。

（2）隱式構造（Implicit Construction）PyTorch/MXNet

在隱式構造（或動態構造）的計算圖中，計算圖是在運行時動態構建的，這意味著每次執行操作時都會實時創建和更新計算圖。程序員無需預先聲明完整的計算圖結構，而是通過直接操作張量（tensor）來進行計算，框架會在背后自動構建和管理計算圖。

例如，在PyTorch中，計算圖是在運行時逐行代碼構建的，當調用一個操作（如加法、矩陣乘法等）時，相應的計算節點和邊會立即加入到計算圖中。這種動態特性使得代碼更加直觀易讀，便于調試和實驗。

總結起來，顯式構造和隱式構造的主要區別在于構建和執行計算圖的時機和方式：
- 顯式構造要求提前定義完整的計算圖結構，執行時按圖進行計算；
- 隱式構造則允許在運行時動態構建和更新計算圖，代碼執行與計算圖構建同步進行，靈活性更高。

參考文章：

機器學習入門（10）— 淺顯易懂的計算圖、鏈式法則講解_請畫出該函數的計算圖,請用方形節點表示-CSDN博客

（先這樣簡單地了解一下是什么，后續可能實際構造會用到……）

（3）兩種求導模式

在這里插入圖片描述

正向累積：執行圖，存儲中間結果
反向累積：從相反方向執行圖，可以去除不需要的枝
復雜度
- n為操作子個數
- 計算復雜度：正反向代價類似，都為 $O (n)$
- 內存復雜度：
  - 反向累積： $O (n)$ ，因為需要存儲正向所有中間結果（深度神經網絡求梯度耗GPU資源）
  - 正向累積： $O (1)$ ，不需要存儲中間結果

Ⅱ自動求導的實現

深度學習框架通過自動計算導數，即自動微分（automatic differentiation）來加快求導。實際中，根據設計好的模型，系統會構建一個計算圖（computational graph），來跟蹤計算是哪些數據通過哪些操作組合起來產生輸出。自動微分使系統能夠隨后反向傳播梯度。這里，反向傳播（backpropagate）意味著跟蹤整個計算圖，填充關于每個參數的偏導數。

自動計算導數的思想：首先將梯度附加到想要對其計算偏導數的變量上，然后記錄目標值的計算，執行它的反向傳播函數，并訪問得到的梯度。

假設相對函數 $y=2\boldsymbol{x}^T\boldsymbol{x}$ 關于列向量 $\boldsymbol{x}$ 求導，運算結果應該為 $4\boldsymbol{x}$ 【數學情況下應該是 $4\boldsymbol{x}^T$ ，但是由于1維的tensor沒有行列之分，所以也等于 $4\boldsymbol{x}$ 】：

import torch
x = torch.arange(4.0)  # 創建變量x并對其分配初始值
x.requires_grad_(True)  # 等價于 x = torch.arange(4.0, requires_grad = True)
y = 2 * torch.dot(x, x) # 結果為tensor(28., grad_fn=<MulBackward0>)
y.backward()  # 啟動反向傳播過程
print(x.grad)   # tensor([ 0.,  4.,  8., 12.])

torch.arange() 函數本身生成的是一維張量（tensor），而不是嚴格意義上的行向量或列向量。這個一維張量可以看作是一個數列，不具備明確的行或列屬性。可以通過 reshape()方法將其轉換為行向量或列向量【二維張量】，或者使用torch.transpose(x1, 0, 1)進行轉置。
x.requires_grad_(True)用于啟用張量 x 上的梯度計算的功能。當一個張量的 requires_grad 屬性被設置為 True 時，意味著在其上的任何操作都會被跟蹤并記錄到計算圖中，以便在反向傳播過程中計算梯度。
grad_fn=<MulBackward0> 表明這個張量是由其他張量經過運算（在這個例子中是乘法操作，由 MulBackward0 指代）產生的，并且參與了反向傳播過程，因此它有梯度信息。這意味著如果對該張量求梯度，框架能夠追溯到之前的運算步驟以計算梯度。如果前面沒有設置啟用梯度計算的功能，則不會顯示該屬性。

葉子節點通常為None，只有結果節點的grad_fn才有效，用于指示梯度函數是哪種類型。
在PyTorch中，y.backward() 是用于啟動反向傳播過程的函數調用，以計算張量 y 相關的所有梯度。當我們處理神經網絡或者其他需要梯度計算的任務時，常常會在前向傳播階段結束并計算出損失函數值后，調用此函數。y.backward() == torch.autograd.backward(y)
多次執行y.backward()會報如下錯誤：

在PyTorch中，每次調用.backward()方法執行反向傳播時，默認情況下會釋放中間計算結果以節省內存。當你再次調用.backward()時，先前的計算圖已經清理掉了，無法再次進行反向傳播。因此，如果你需要在同一個計算圖上多次執行反向傳播，你需要在.backward()調用時添加參數retain_graph=True，這樣PyTorch就會保留計算圖，直到顯式清除它為止。

但是頻繁地保留計算圖可能會占用大量的內存資源，尤其是在復雜的模型中。通常，你應在完成多次反向傳播之后手動清空不需要的梯度，以避免內存泄漏：x.grad.zero_()，得到一個全零張量。

如果不調用清除梯度值的函數，當我們調用 y.backward(retain_graph=True) 并且多次執行時，x.grad 會不斷變化的原因在于每次執行反向傳播時，新的梯度會累積到現有的梯度之上。由于設置了 retain_graph=True，即使在多次調用 .backward() 后，也不會清除原有的計算圖，使得可以不斷地在原有基礎上累加梯度。

例如，假設第一次執行反向傳播時，計算出 x 對 y 的梯度為 dx1，第二次反向傳播時，又計算出梯度為 dx2，那么兩次之后 x.grad 將會是 dx1 + dx2。
backward()的作用一直都是求出某個張量對于某些標量節點的梯度。注意非標量變量反向傳播的計算，注意backward()中的參數：

Pytorch autograd,backward詳解

分離計算

有時，我們希望將某些計算移動到記錄的計算圖之外。例如，假設y是作為x的函數計算的，而z則是作為y和x的函數計算的。當我們想計算z關于x的梯度，但由于某種原因，希望將y視為一個常數，并且只考慮到x在y被計算后發揮的作用。

這里可以使用u=y.detach()分離y來返回一個新變量u，該變量與y具有相同的值，但丟棄計算圖中如何計算y的任何信息。換句話說，梯度不會向后流經u到x。因此，下面的反向傳播函數計算z=u*x關于x的偏導數，同時將u作為常數處理，而不是z=x*x*x關于x的偏導數。

x.grad.zero_()
y = x * x
u = y.detach() #用于從計算圖中分離一個張量，這意味著對 .detach() 后得到的新張量所做的任何操作都不會影響原始計算圖中的梯度計算。
# u 是 y 的副本，但它與原來的計算圖斷開了聯系，即 u 的梯度不會回傳到 x
z = u * xz.sum().backward()
x.grad == u  # tensor([True, True, True, True])

計算二階導的參考方法：

在 PyTorch 中，雖然自動求導機制主要用于一階導數的計算，但通過組合現有的一階導數和 PyTorch 提供的功能，可以間接計算二階導數，即 Hessian 矩陣或其他二階導數相關的信息。

對于一個可微分函數 f(x)，如果你有一個張量 x 并且 x.requires_grad=True，你可以先通過 .backward() 計算一階導數（梯度）。然后，如果你想計算二階導數（例如 Hessian 矩陣），通常需要執行以下步驟：
計算一階導數：
x = torch.randn(size=(n,), requires_grad=True)
y = f(x)# 假設 f 是基于 x 的某些操作組成的函數
y.backward()# 計算 y 關于 x 的梯度，存儲在 x.grad 中
保存一階導數：在計算二階導數之前，你需要保存第一次求導得到的一階導數，因為接下來的第二次求導會覆蓋這些值。
first_derivative = x.grad.clone().detach()
計算二階導數：對于每個元素的 Hessian 矩陣，可以通過對一階導數再次求導來獲得。但在實際操作中，由于內存限制和計算效率問題，直接計算整個 Hessian 矩陣通常是不可行的，尤其是對于大規模神經網絡。因此，常常采用逐元素或者稀疏的方式估算 Hessian-vector 乘積，或者采用近似方法（如有限差分法）。
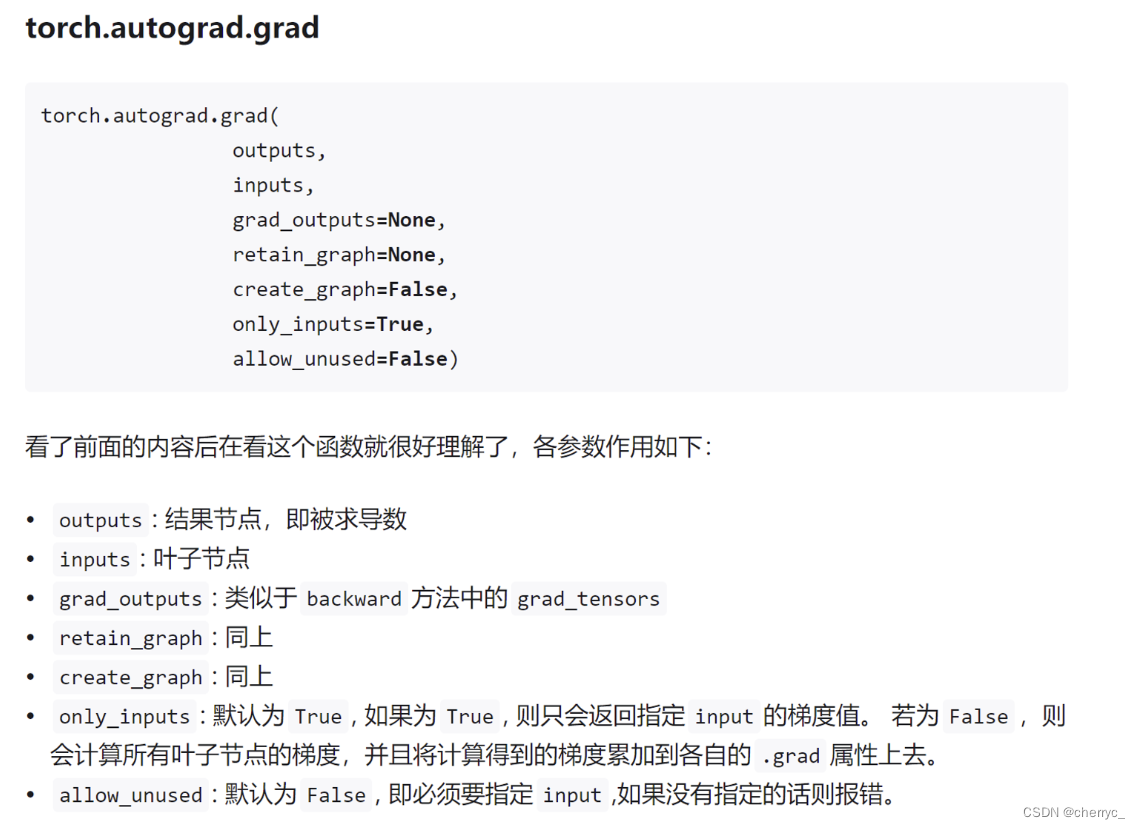
# 創建一個與 x 形狀相同的張量作為“方向向量”
v = torch.randn_like(x, requires_grad=False)# 將一階導數當作中間變量，并計算關于它的梯度
# 這里是對一階導數求導，相當于得到 Hessian-vector 乘積
x.grad.zero_()
torch.autograd.grad(outputs=first_derivative, inputs=x, grad_outputs=v, retain_graph=True, create_graph=True)[0].view_as(v)
上述代碼中的 retain_graph=True 參數確保在計算完成后原始計算圖不會被釋放，以便進行多次反向傳播。而 create_graph=True 則意味著在進行這次反向傳播時也記錄新的計算圖，使得能夠對新得到的梯度再求導。
如果確實需要計算完整的 Hessian 矩陣，可能需要借助第三方庫，或者編寫循環結構來分別計算每一項。不過請注意，這樣的操作在計算資源和時間開銷上往往非常昂貴，特別是在高維度情況下。對于大型模型，研究者更傾向于使用更有效率的二階優化方法或二階信息的近似。

👌使f(x)=sin(x)，繪制f(x)和df(x)/dx的圖像：

import torch
import matplotlib.pyplot as plt# 創建可微分的張量
x = torch.arange(0., 10., 0.1, requires_grad=True)
y = torch.sin(x)# 計算 y 的總和，并反向傳播得到 dy/dx
y_sum = y.sum()
y_sum.backward()# 將 PyTorch 張量轉換為 NumPy 數組以便 Matplotlib 繪圖
x_np = x.detach().numpy()
y_np = y.detach().numpy()
# 不能將具有 requires_grad=True 屬性的 PyTorch 張量直接轉換為 NumPy 數組。
# 在需要進行反向傳播的計算過程中，這樣的張量不能直接轉換成 NumPy 數組，因為它們包含了梯度信息。
# 解決這個問題的方法是在轉換之前使用 .detach() 方法斷開張量與計算圖的連接，使其不再跟蹤梯度。
dy_dx_np = x.grad.numpy()# 分別繪制正弦函數和它的導數
plt.plot(x_np, y_np, label='y')
plt.plot(x_np, dy_dx_np, label='dy/dx')# 添加圖例和顯示圖形
plt.legend()
plt.show()