🚀個人主頁：為夢而生~ 關注我一起學習吧！
💡專欄：機器學習 歡迎訂閱！相對完整的機器學習基礎教學！
?特別提醒：針對機器學習，特別開始專欄：機器學習python實戰 歡迎訂閱！本專欄針對機器學習基礎專欄的理論知識，利用python代碼進行實際展示，真正做到從基礎到實戰！
💡往期推薦：
【機器學習基礎】一元線性回歸（適合初學者的保姆級文章）
【機器學習基礎】多元線性回歸（適合初學者的保姆級文章）
【機器學習基礎】決策樹（Decision Tree）
【機器學習基礎】K-Means聚類算法
【機器學習基礎】DBSCAN
【機器學習基礎】支持向量機
【機器學習基礎】集成學習
💡本期內容：BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）是一種用于大規模數據集的層次聚類算法。它采用一種多層次的聚類方法，首先利用一種稱為“聚類特征樹（CF Tree）”的數據結構來壓縮數據集，然后通過逐步分裂每個節點以形成聚類。

---

---

1 引言

1.1 聚類分析的重要性和應用場景

聚類分析是一種重要的數據分析技術，其重要性和應用場景主要體現在以下幾個方面：

重要性：

1. 發現隱藏模式與規律：聚類分析能夠幫助我們從大量數據中發現隱含的模式和規律，從而提高數據的利用價值。
2. 數據預處理：聚類分析經常作為數據挖掘的預處理步驟，將數據轉化為更適合分類或回歸的形式。
3. 自動分組：它是一種無監督學習方法，能夠自動對數據進行分組，將相似的數據歸為同一組，不相似的數據歸為不同的組。

應用場景：

1. 商業智能分析：聚類分析可以將客戶群體分成不同的類別，從而幫助企業開展更有針對性的營銷活動。例如，市場分析人員可以通過聚類分析從客戶數據庫中識別出不同的客戶群，并使用購買模式來描述這些客戶群的特征。
2. 電商購物推薦：聚類分析可以將相似的用戶或商品聚類在一起，使得推薦系統能夠提供更精準的推薦服務。
3. 生物信息學：聚類分析可以用于推導植物和動物的分類，對基因進行分析，從而幫助科學家獲得對種群中固有結構的認識。
4. 圖像分析：聚類分析可以用于圖像分割和識別，幫助我們從復雜的圖像中識別出不同的對象或特征。
5. 社會網絡分析：聚類分析可以幫助我們識別社會網絡中的不同群體或社區，從而更好地理解網絡結構。
6. 時序數據分析和復雜網絡社團發現：聚類分析也可以應用于時序數據分析和復雜網絡的社團發現，幫助我們從大量數據中提取有用的信息。

1.2 層次聚類和BIRCH聚類的發展背景

層次聚類（Hierarchical Clustering）是一種聚類分析方法，它的基本思想是將數據集中的樣本看作一棵樹的葉子，然后通過不斷合并或分裂葉子節點，形成一棵聚類樹。

這棵樹的每一個內部節點表示一個聚類，而葉子節點表示單個的樣本。根據聚類方式的不同，層次聚類可以分為凝聚的層次聚類和分裂的層次聚類。

凝聚的層次聚類是自底向上的方法，開始時將每個樣本看作一個聚類，然后不斷合并最近的聚類，直到滿足某個終止條件；而分裂的層次聚類則是自頂向下的方法，開始時將所有樣本看作一個聚類，然后不斷分裂最遠的樣本，直到滿足某個終止條件。

BIRCH算法是在1996年由Tian Zhang提出來的，它是一種基于距離的層次聚類方法，綜合了層次凝聚和迭代的重定位方法。層次凝聚是采用自底向上策略，將每個對象作為一個原子簇，然后合并這些原子簇形成更大的簇，減少簇的數目，直到所有的對象都在一個簇中或滿足某個終結條件。

隨著大數據時代的到來，處理大規模數據集成為了聚類算法的重要挑戰之一。BIRCH算法作為一種高效的層次聚類方法，在處理大規模數據集時具有顯著的優勢。它能夠有效地利用有限的內存資源完成高質量的聚類，并且可以通過單遍掃描數據集來最小化I/O代價。因此，BIRCH算法在各個領域得到了廣泛的應用和研究。

總之，BIRCH算法是一種基于層次的聚類方法，通過使用聚類特征和聚類特征樹來概括和存儲聚類信息，從而實現了高效且高質量的聚類。它在處理大規模數據集時具有顯著的優勢，并且可以廣泛應用于各個領域的聚類分析問題中。

---

2 層次聚類概述

2.1 層次聚類的定義及其基本思想

層次聚類的定義：

層次聚類（Hierarchical Clustering）是一種聚類算法，它的核心思想是通過計算不同類別數據點間的相似度來創建一棵有層次的嵌套聚類樹。在這棵聚類樹中，不同類別的原始數據點是樹的最低層，而樹的頂層是一個聚類的根節點。這種聚類方法可以看作是一個樹狀的聚類結構，數據點或聚類從下到上不斷被合并，或者從上到下不斷被分裂。

層次聚類的基本思想：

層次聚類通過某種相似性測度計算節點之間的相似性，并按相似度由高到低排序。根據聚類方式的不同，可以分為凝聚的層次聚類和分裂的層次聚類。

1. 凝聚的層次聚類（自下而上的方法）：開始時，每個樣本或數據點都被視為一個單獨的聚類。然后，算法計算所有聚類之間的距離或相似度，并選擇最近或最相似的兩個聚類進行合并。這個過程不斷重復，直到所有的聚類合并為一個，或者達到預設的聚類數目，或者聚類之間的距離超過某個閾值。
2. 分裂的層次聚類（自上而下的方法）：與凝聚的方法相反，開始時，所有的樣本或數據點都被視為一個單一的聚類。然后，算法選擇距離最遠或最不相似的樣本對，并將它們分別分裂為新的聚類。這個過程不斷重復，直到每個聚類中只有一個樣本，或者達到預設的聚類數目，或者樣本之間的距離小于某個閾值。

層次聚類的優點在于它可以隨時停止劃分，并且能夠形成層次結構，使用戶可以觀察和理解數據的不同層次的結構。然而，由于它需要計算所有樣本或聚類之間的距離或相似度，因此在處理大規模數據集時可能會變得非常耗時。

2.2 層次聚類的優缺點分析

優點：

1. 能夠發現類的層次關系：層次聚類可以通過合并或分裂操作，逐步構建或細化聚類結構，從而展示數據點之間的層次關系。這對于理解數據的組織結構非常有幫助。
2. 對樣本輸入順序不敏感：與一些其他聚類算法相比，層次聚類對樣本的輸入順序不太敏感，這意味著即使改變樣本的輸入順序，聚類結果也可能保持相對穩定。
3. 能夠處理任意形狀的聚類：層次聚類不依賴于數據的分布假設，因此它可以處理各種形狀的聚類，包括非凸形狀和復雜結構。

缺點：

1. 計算復雜度較高：層次聚類需要計算所有樣本或聚類之間的距離或相似度，這導致它在處理大規模數據集時可能變得非常耗時。此外，合并或分裂操作也可能導致計算量的增加。
2. 可能形成鏈狀聚類：在某些情況下，層次聚類可能會形成鏈狀結構，即一些聚類在合并過程中可能會成為其他聚類的子聚類，這可能導致聚類結果的不穩定或難以解釋。
3. 聚類終止條件難以確定：層次聚類需要指定一個終止條件來確定何時停止合并或分裂操作。然而，確定這個條件可能是一個困難的任務，因為不同的終止條件可能會導致不同的聚類結果。

---

3 BIRCH聚類算法介紹

3.1 BIRCH算法的基本概念

BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）聚類是一種增量式的層次聚類方法。

它通過使用一個叫做CF Tree（聚類特征樹）的樹結構來概括聚類特征，從而實現有效的聚類和規約。

BIRCH聚類的主要優點是它可以處理大規模的數據集，并且對異常值有很好的魯棒性。它通過將數據集中的點進行聚類，將分布在稠密區域中的點聚為一類，而將分布在稀疏區域中的點視為異常點進行移除。

此外，BIRCH聚類是一種增量式的聚類方法，這意味著它可以在處理新數據時，基于已經處理過的數據點進行聚類決策，而不是重新計算所有的數據點。

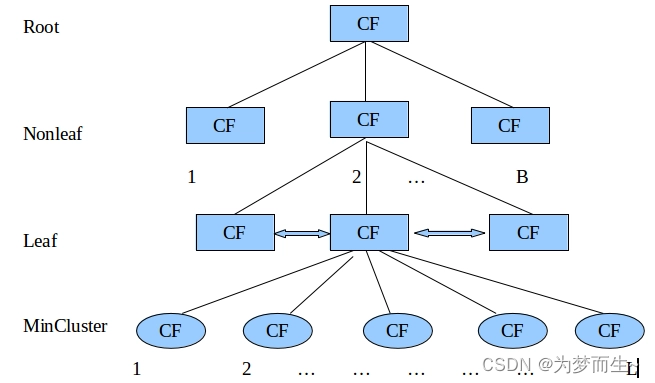
3.2 BIRCH算法的核心思想：使用樹狀結構（CF Tree）存儲和聚類數據

BIRCH算法的核心思想使用樹狀結構（CF Tree，即聚類特征樹）來存儲和聚類數據。這種樹狀結構的設計使得算法能夠有效地處理大規模數據集，同時保持聚類的質量和效率。

CF Tree中的每個節點都由一個或多個聚類特征（CF）組成，這些CF是算法用于概括和存儲聚類信息的關鍵。CF是一個三元組，包括簇中樣本點的數量、各特征維度的和向量以及各特征維度的平方和，它用于存儲關于簇的基本信息，同時實現了數據的壓縮。

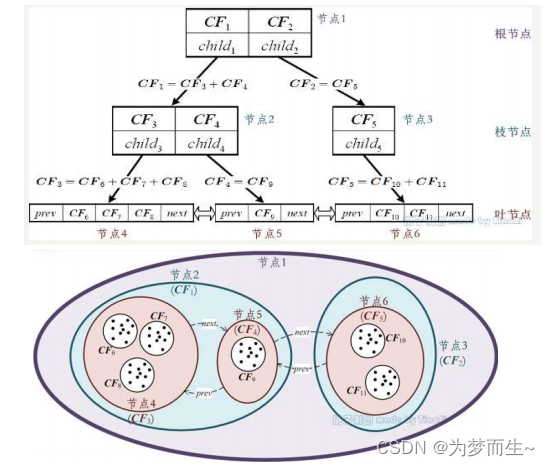
通過CF Tree，BIRCH算法可以在有限的內存資源下進行高質量的聚類。算法通過不斷插入新的數據點，并根據CF Tree的結構進行聚類的合并和分裂，從而逐步構建出完整的聚類結構。此外，由于CF Tree的高度平衡性，算法可以在對數時間內完成聚類操作，進一步提高了聚類的效率。

因此，使用樹狀結構（CF Tree）來存儲和聚類數據是BIRCH算法的核心思想，這種思想使得算法在處理大規模數據集時具有顯著的優勢，并且廣泛應用于各個領域的聚類分析問題中。

3.3 聚類特征樹（CF Tree）的生成

1. 從根節點root 開始遞歸往下，計算當前CF條目與要插入數據點之間的距離，尋找距離最小的那個路徑，直到找到與該數據點最接近的葉節點中的條目。
2. 比較計算出的距離是否小于閾值T，如果小于則當前CF條目吸收該數據點，并更新路徑上的所有CF三元組；反之，進行第三步。
3. 判斷當前條目所在葉節點的CF條目個數是否小于λ，如果是，則直接將數據點插入作為該數據點的新條目，否則需要分裂該葉節點。分裂的原則是尋找該葉節點中距離最遠的兩個CF條目并以這兩個CF條目作為種子，其他剩下的CF條目根據距離最小原則分配到這兩個簇中，并更新整個CF樹。
4. 依次向上檢查父節點是否也要分裂，如果需要按和葉子節點分裂方式相同。

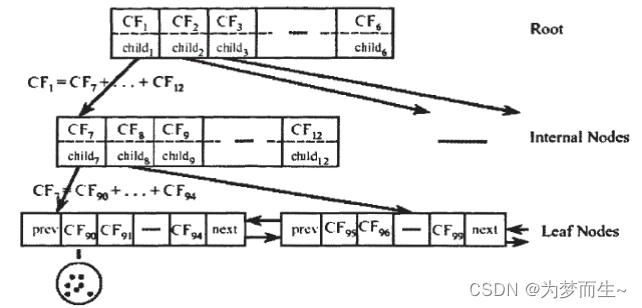
先定義好CF Tree的參數： 即枝平衡因子β（內部節點的最大CF數）， 葉平衡因子λ（葉子節點的最大CF數），空間閾值τ（ 葉節點每個CF的最大樣本半徑或直徑）

在最開始的時候，CF Tree是空的，沒有任何樣本，我們從訓練集讀入第一個樣本點，將
它放入一個新的CF三元組A，這個三元組的N=1，將這個新的CF放入根節點

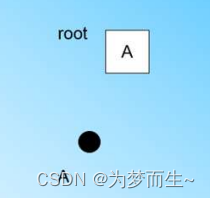
繼續讀入第二個樣本點，我們發現這個樣本點和第一個樣本點A，在半徑為T的超球體范圍內，也就是說，他們屬于一個CF，我們將第二個點也加入CF A,此時需要更新A的三元組的值。此時A的三元組中N=2，如下圖一

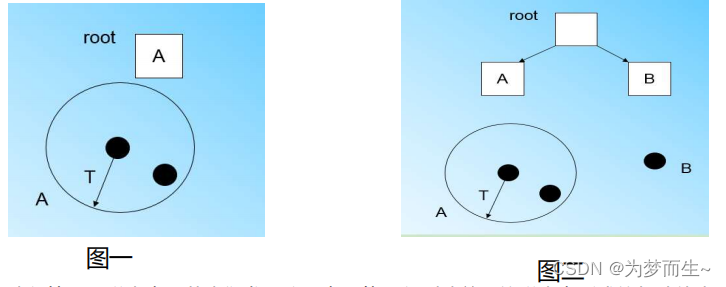
讀入第三個樣本點，若我們發現這個點不能融入剛才前面的樣本點形成的超球體內，就需要
一個新的CF三元組B。此時根節點有兩個CF三元組A和B，如上圖二

讀入第四個樣本點，若發現和B在半徑小于T的超球體內，繼續更新

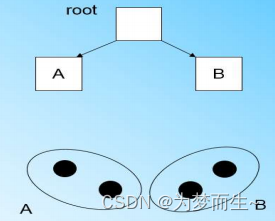
什么時候CF Tree的節點需要分裂呢？

假設我們現在的CF Tree 如下圖， 節點LN1有三個CF， LN2和LN3各有兩個CF。我們的葉子節點的最大CF數λ=3。此時一個新的樣本點來了，計算得出它離LN1中的葉子節點最近，那么開始判斷它是否在sc1,sc2,sc3。這3個CF對應的超球體之內，因不在，故需要建立一個新的CF，即sc8來容納它。

但我們的λ=3，也就是說LN1的CF個數已經達到最大值了，不能再創建新的CF了，此時就要將LN1節點一分為二了

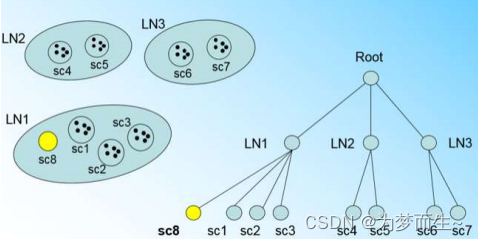
將LN1里所有CF元組中，找到兩個最遠的CF做為種子CF，然后將LN1節點里所有CF 即sc1, sc2, sc3，以及新樣本點的新元組sc8劃分到兩個新的節點上。將LN1節點劃分后的CF Tree如下圖

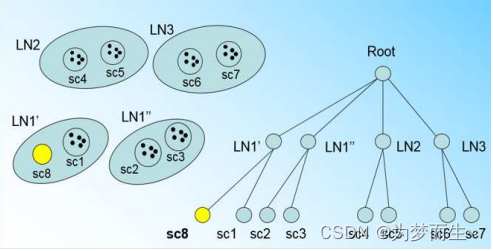
若內部節點的最大CF數β=3，則此時會導致最大CF數超了，也就是說要繼續，方法與前面一樣，分裂后的CF Tree如下圖

---

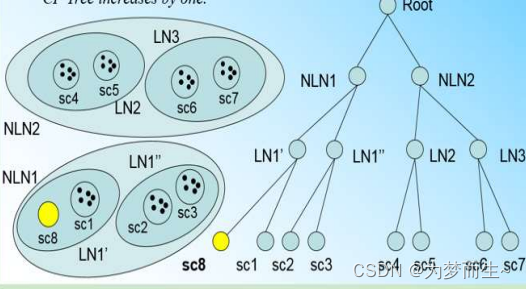
4 BIRCH聚類算法的優勢和局限性

算法優點

1. 節省內存。葉子節點放在磁盤分區上，非葉子節點僅僅是存儲了一個CF值，外加指向父節點和孩子節點的指針。
2. 快, 計算兩個簇的距離只需要用到(N,LS,SS)這三個值足矣。
3. 只需掃描一遍數據集即可建樹。
4. 可識別噪聲點。建立好CF樹后把那些包含數據點少的子簇剔除。

算法缺點

1. 結果依賴于數據點的插入順序。
2. 對非球狀的簇聚類效果不好。

---

5 BIRCH聚類算法的應用實例

1. 社交網絡分析：在社交網絡中，用戶的行為和關系可以形成大規模的數據集。使用BIRCH聚類算法，可以有效地識別出社交網絡中的不同群體或社區，從而幫助研究人員或企業更好地理解用戶行為，優化產品設計或服務。
2. 電商推薦系統：在電商領域，用戶的歷史購買記錄、瀏覽記錄等行為數據可以形成大規模的數據集。通過應用BIRCH聚類算法，可以將相似的用戶或商品聚類在一起，從而實現更精準的推薦服務。同時，算法還可以幫助商家發現潛在的客戶群體和市場趨勢。
3. 金融風險管理：在金融領域，大量的交易數據、客戶信息等數據需要進行有效的分析和處理。BIRCH聚類算法可以幫助金融機構識別出異常交易或客戶行為，從而及時發現和防范金融風險。
4. 圖像分割和識別：在圖像處理領域，BIRCH聚類算法可以用于圖像分割和識別。算法可以將圖像中的像素或區域聚類在一起，從而形成不同的對象或特征。這有助于實現更準確的圖像識別和目標檢測。