給你一個整數?n?表示一棵?滿二叉樹?里面節點的數目，節點編號從?1?到?n?。根節點編號為?1?，樹中每個非葉子節點?i?都有兩個孩子，分別是左孩子?2 * i?和右孩子?2 * i + 1?。

樹中每個節點都有一個值，用下標從?0?開始、長度為?n?的整數數組?cost?表示，其中?cost[i]?是第?i + 1?個節點的值。每次操作，你可以將樹中?任意?節點的值?增加?1?。你可以執行操作?任意?次。

你的目標是讓根到每一個?葉子結點?的路徑值相等。請你返回?最少?需要執行增加操作多少次。

注意：

• 滿二叉樹?指的是一棵樹，它滿足樹中除了葉子節點外每個節點都恰好有 2 個子節點，且所有葉子節點距離根節點距離相同。
• 路徑值?指的是路徑上所有節點的值之和。

示例 1：

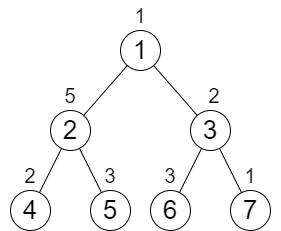
輸入：n = 7, cost = [1,5,2,2,3,3,1]
輸出：6
解釋：我們執行以下的增加操作：
- 將節點 4 的值增加一次。
- 將節點 3 的值增加三次。
- 將節點 7 的值增加兩次。
從根到葉子的每一條路徑值都為 9 。
總共增加次數為 1 + 3 + 2 = 6 。
這是最小的答案。

示例 2：

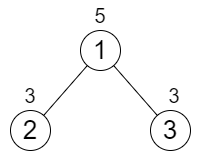
輸入：n = 3, cost = [5,3,3]
輸出：0
解釋：兩條路徑已經有相等的路徑值，所以不需要執行任何增加操作。

提示：

• 3 <= n <= 105
• n + 1?是?2?的冪
• cost.length == n
• 1 <= cost[i] <= 104

題解：

code:

class Solution {public int minIncrements(int n, int[] cost) {int ans = 0;for (int i = n - 2; i > 0; i -= 2) {ans += Math.abs(cost[i] - cost[i + 1]);// 葉節點 i 和 i+1 的雙親節點下標為 i/2（整數除法）cost[i / 2] += Math.max(cost[i], cost[i + 1]);}return ans;}
}