一、引入
希爾排序是一種分組插入排序的算法。
二、排序思路
- 首先取一個整數d1 = n/2,將元素分為d1個組,每組相鄰量取元素距離為d1,在各組內直接進行插入排序;
- 取第二個整數d2 = d1/2, 重復上述分組排序過程,直到d1 = 1,即所有元素在同意最內進行直接插入排序。
- 希爾排序每趟并不使某些元素有序,而是使整體數據越來越接近有序;最后一趟排序使得所有數據有序。
如下圖所示:n = 9 ; d1 = n // 2 = 4 ; 第一次將其分為四組;每組進行一次插入排序,排序完成后返回。
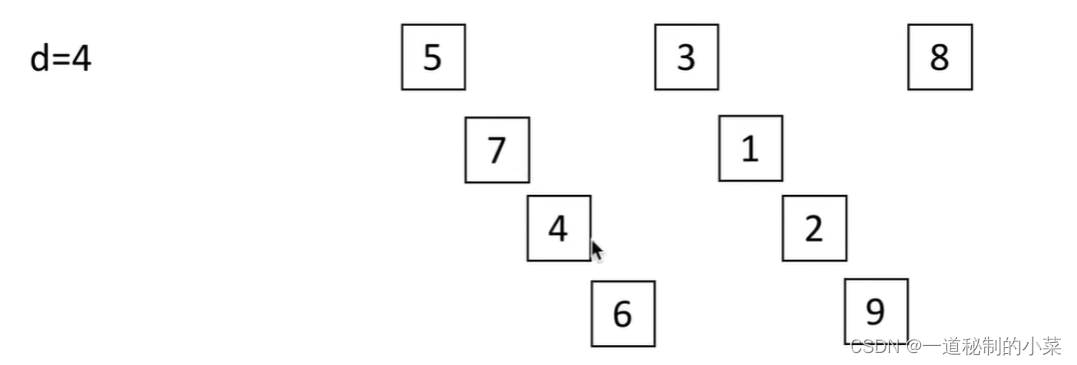
第二次將其分為 d1 = d // 2? = 2組后再重新進行插入排序:
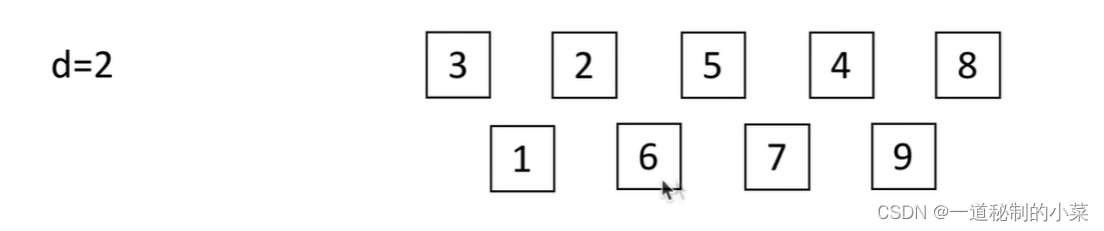
直到最后d = 1時,再對整體進行一次插入排序
 ?
?
三、代碼思路
1. 按照間隔為gap的插入

相當于每次間隔gap進行一次插入排序,對比之前寫的插入排序,相當于將其中的1變為gap。
示例代碼:
def insert_sort_gap(li, gap):for i in range(gap, len(li)): # i 表示摸到牌的下表; 總共n張牌,起始手里有一張牌tmp = li[i] # 將摸到的牌存起來j = i - gap # j指的是手里牌的下標,初始手里有一張牌while j >= 0 and li[j] > tmp: # 將手里的牌和摸到的牌作比較;摸到的牌小于手里的牌andli[j + gap] = li[j] # 往右挪位置j -= gap # 縮小j后繼續比較li[j + gap] = tmp # j往前移后繼續比較;如果此時摸到的牌大于li[j],則將摸到的牌放到j+1的位置print(li)?接下來我們再寫希爾排序的代碼:
def shell_sort(li):d = len(li) // 2while d >= 1 :insert_sort_gap(li, d)d //= 2因此總的演示代碼如下所示:
def insert_sort_gap(li, gap):for i in range(gap, len(li)): # i 表示摸到牌的下表; 總共n張牌,起始手里有一張牌tmp = li[i] # 將摸到的牌存起來j = i - gap # j指的是手里牌的下標,初始手里有一張牌while j >= 0 and li[j] > tmp: # 將手里的牌和摸到的牌作比較;摸到的牌小于手里的牌andli[j + gap] = li[j] # 往右挪位置j -= gap # 縮小j后繼續比較li[j + gap] = tmp # j往前移后繼續比較;如果此時摸到的牌大于li[j],則將摸到的牌放到j+1的位置def shell_sort(li):d = len(li) // 2while d >= 1 :insert_sort_gap(li, d)d //= 2li = [1,4,7,2,5,8,3,6,9]
print(li)
shell_sort(li)
print(li)輸出結果如下:
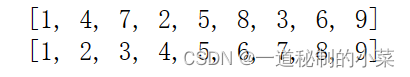
四、時間復雜度
希爾排序的時間復雜度比較復雜,并且和選取的gap序列有關。?

 ?
?
如上圖所示,選取不同的gap序列時希爾排序具有不同的時間復雜度,且存在一些復雜的gap序列使得無法計算其復雜度,但總的來說,希爾排序的時間復雜度比基礎排序快,比進階排序慢。?
?
?
?
?
?

)






:滾動彈幕的設計與實現)










