近年來,隨著Transformer、MOE架構的提出,使得深度學習模型輕松突破上萬億規模參數,從而導致模型變得越來越大,因此,我們需要一些大模型壓縮技術來降低模型部署的成本,并提升模型的推理性能。
模型壓縮主要分為如下幾類:
- 剪枝(Pruning)
- 知識蒸餾(Knowledge Distillation)
- 量化Quantization)
本系列將針對一些常見大模型量化方案(GPTQ、LLM.int8()、SmoothQuant、AWQ等)進行講述。
- 大模型量化概述
- 量化感知訓練:
- 大模型量化感知訓練技術原理:LLM-QAT
- 大模型量化感知微調技術原理:QLoRA
- 訓練后量化:
- 大模型量化技術原理:GPTQ、LLM.int8()
- 大模型量化技術原理:SmoothQuant
- 大模型量化技術原理:AWQ、AutoAWQ
- 大模型量化技術原理:SpQR
- 大模型量化技術原理:ZeroQuant系列
- 大模型量化技術原理:總結
而本文主要針對大模型量化技術 SmoothQuant 進行講述。
另外,我撰寫的大模型相關的博客及配套代碼均整理放置在Github:llm-action,有需要的朋友自取。
背景
LLM.int8() 發現當 LLMs 的模型參數量超過 6.7B 的時候,激活中會成片的出現大幅的離群點(outliers),樸素且高效的量化方法(W8A8、ZeroQuant等)會導致量化誤差增大,精度下降。
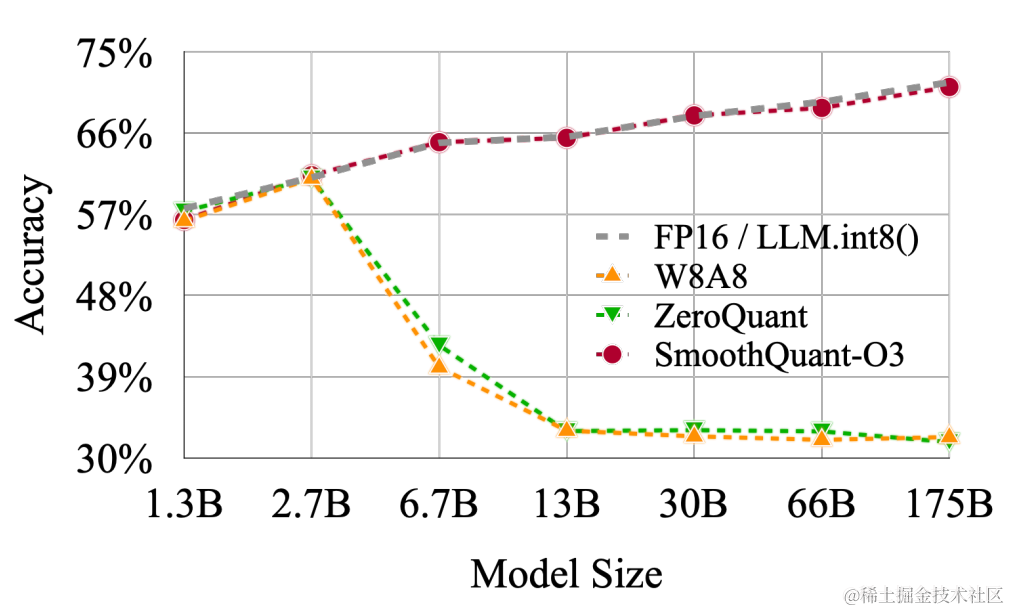
但好在新出現的離群特征(Emergent Features)的分布是有規律的。通常,這些離群特征只分布在 Transformer 層的少數幾個維度。針對這個問題,LLM.int8() 采用了混合精度分解計算的方式(離群點和其對應的權重使用 FP16 計算,其他量化成 INT8 后計算)。雖然能確保精度損失較小,但由于需要運行時進行異常值檢測、scattering 和 gathering,導致它比 FP16 推理慢。
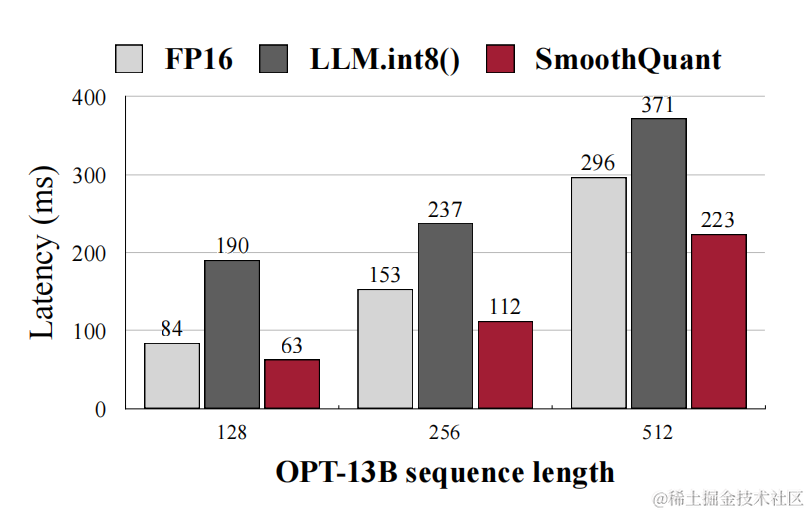
這些激活上的離群點會出現在幾乎所有的 token 上但是局限于隱層維度上的固定的 channel 中;給定一個 token,不同 channels 間的方差會很大,但是對于不同的 token,相同 channel 內的方差很小。考慮到激活中的這些離群點通常是其他激活值的 100 倍,這使得激活量化變得困難。
以上是大模型量化困難的原因,總結下來就三點:
- 激活比權重更難量化(之前的工作LLM.int8()表明,使用 INT8 甚至 INT4 量化 LLM 的權重不會降低準確性。)
- 異常值讓激活量化更困難(激活異常值比大多數激活值大約 100 倍。 如果我們使用 INT8 量化,大多數值將被清零。)
- 異常值持續存在于固定的通道(channel)中(固定通道存在異常值,并且異常值通道值較大)
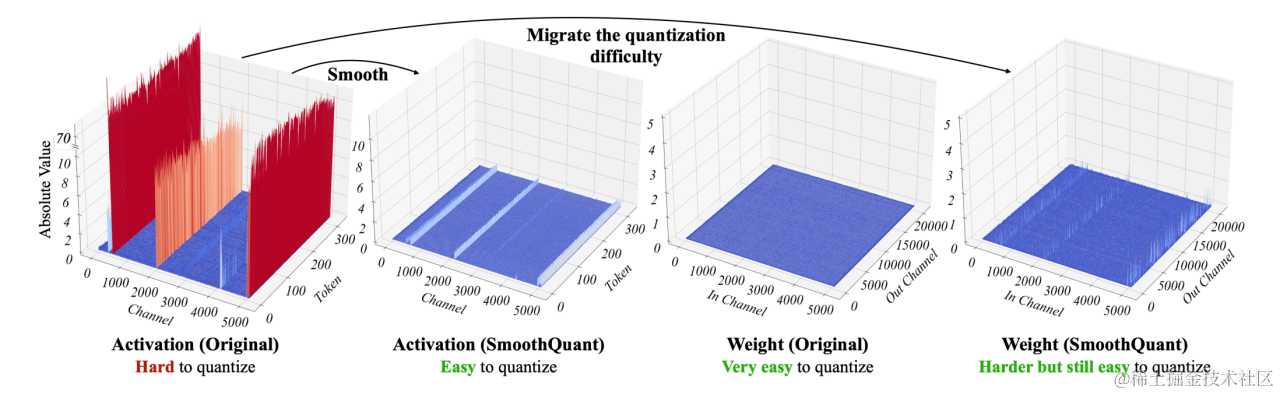
根據量化參數s(數據量化的間隔)和z(數據偏移的偏置)的共享范圍,即量化粒度的不同,量化方法可以分為逐層量化(per-tensor)、逐通道(per-token & per-channel 或者 vector-wise quantization )量化和逐組量化(per-group、Group-wise)。
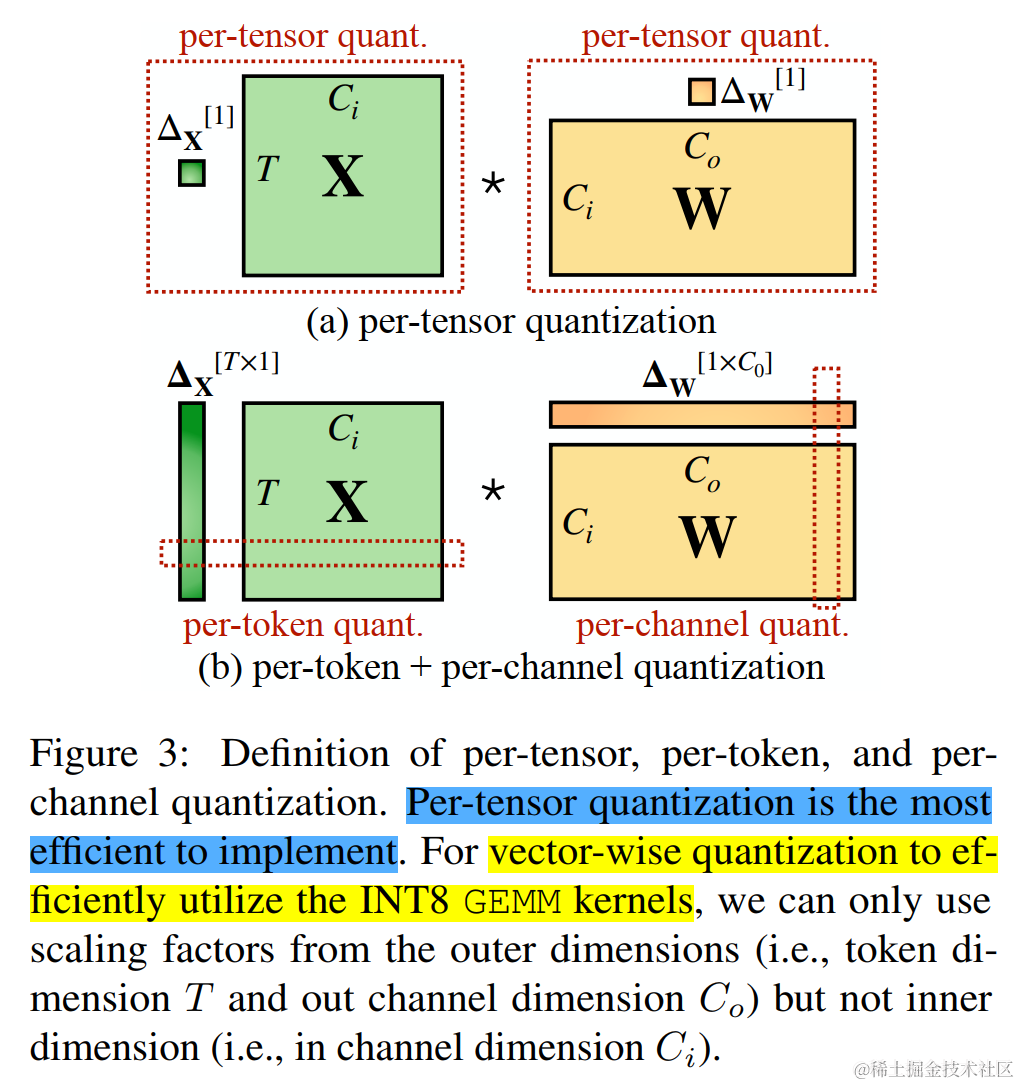
作者對比了 per-channel、per-token、per-tensor 激活量化方案。在這幾種不同的激活量化方案中。per-tensor量化是最高效的實現方式。但只有逐通道量化(per-channel)保留了精度,因它與 INT8 GEMM 內核不兼容。即per-channel量化不能很好地映射到硬件加速的GEMM內核(硬件不能高效執行,從而增加了計算時間)。
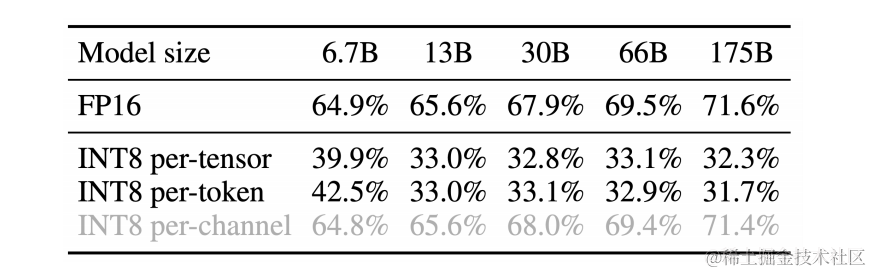
為了進行 vector-wise quantization 以有效利用 INT8 GEMM 內核,我們只能使用外部維度(即Token維度 T 和 通道外維度 C 0 C_0 C0?)的縮放因子,不能使用內部維度(即通道內維度 C i C_i Ci?),因此,先前的工作對激活都采用了per-token量化,但并不能降低激活的難度。
于是 SmoothQuant 提出了一種數學上等價的逐通道縮放變換(per-channel scaling transformation),可顯著平滑通道間的幅度,從而使模型易于量化,保持精度的同時,還能夠保證推理提升推理速度。
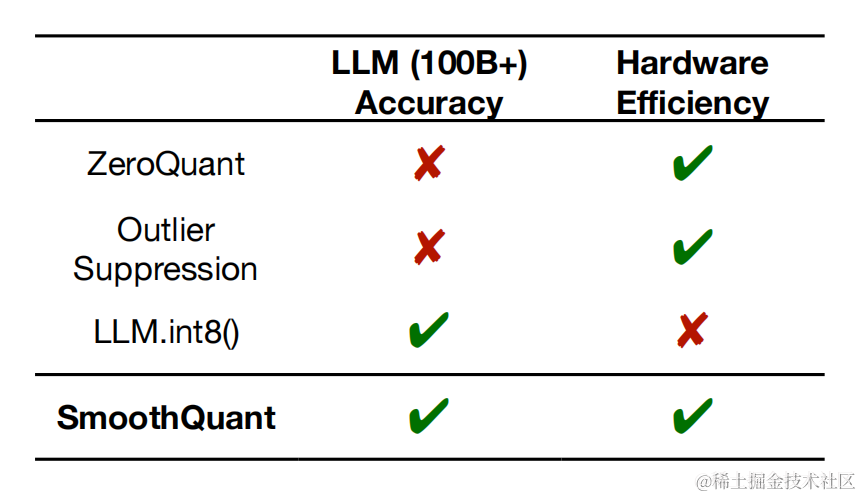
SmoothQuant 技術原理
SmoothQuant (論文:SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models)是一種同時確保準確率且推理高效的訓練后量化 (PTQ) 方法,可實現 8 比特權重、8 比特激活 (W8A8) 量化。由于權重很容易量化,而激活則較難量化,因此,SmoothQuant 引入平滑因子s來平滑激活異常值,通過數學上等效的變換將量化難度從激活轉移到權重上。
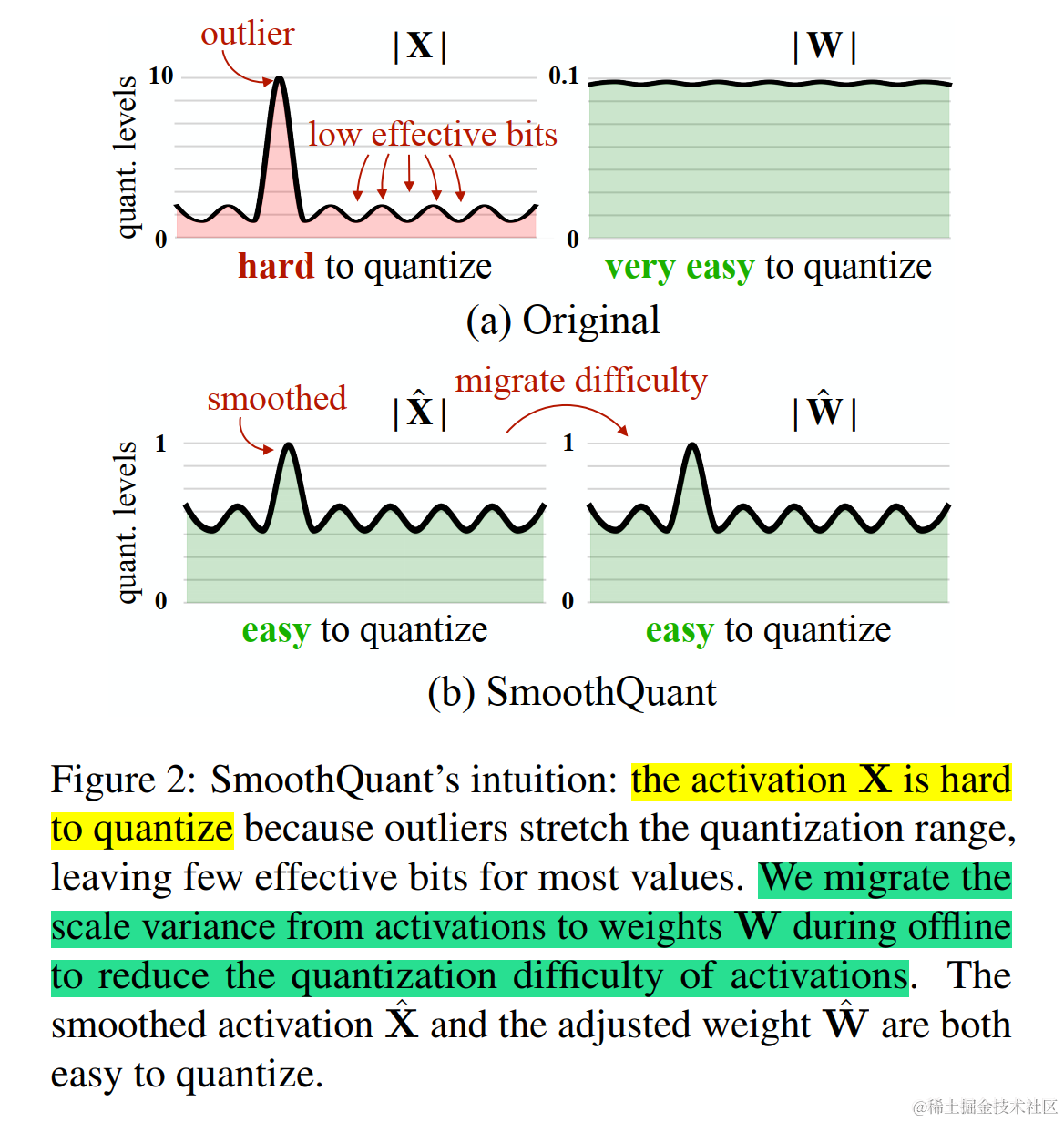
常規的矩陣乘如下:
Y = X W Y=XW Y=XW
SmoothQuant 對激活進行 smooth,按通道除以 smoothing factor。為了保持線性層數學上的等價性,以相反的方式對權重進行對應調整。SmoothQuant 的矩陣乘如下:
Y = ( X d i a g ( s ) ? 1 ) ? ( d i a g ( s ) ? 1 W ) = X ^ W ^ Y=(Xdiag(s)^{-1}) \cdot (diag(s)^{-1}W)=\hat{X} \hat{W} Y=(Xdiag(s)?1)?(diag(s)?1W)=X^W^
$X \in R ^{T \times C_i} $ 在 channel 維度(列)上每個元素除以? s i s_i si??,$ W \in R ^{ C_i \times C_0} 則在每行上每個元素乘以? 則在每行上每個元素乘以? 則在每行上每個元素乘以?s_i$ 。這樣?Y 在數學上是完全相等的,平滑因子s的計算公式下面會講述。
將量化難度從激活遷移到權重
為了減小量化誤差,可以為所有 channels 增加有效量化 bits。當所有 channels 都擁有相同的最大值時,有效量化 bits 將會最大。
一種做法是讓? s j = m a x ( ∣ X j ∣ ) , j = 1 , 2 , . . . , C j s_j=max(|X_j|),j=1,2,...,C_j sj?=max(∣Xj?∣),j=1,2,...,Cj? ,? C j C_j Cj??代表第 j 個 input channel。各 channel 通過除以? s j s_j sj??后,激活 channels 都將有相同的最大值,這時激活比較容易量化。但是這種做法會把激活的量化難度全部轉向權重,導致一個比較大的精度損失。
另一種做法是讓 s j = 1 / m a x ( ∣ W j ∣ ) s_j=1/max(|W_j|) sj?=1/max(∣Wj?∣),這樣權重 channels 都將有相同的最大值,權重易量化,但激活量化誤差會很大。
因此,我們需要在 weight 和 activation 中平衡量化難度,讓彼此均容易被量化。本文作者通過加入一個超參?$ \alpha (遷移強度),來控制從激活值遷移多少難度到權重值。一個合適的遷移強度值能夠讓權重和激活都易于量化。 (遷移強度),來控制從激活值遷移多少難度到權重值。一個合適的遷移強度值能夠讓權重和激活都易于量化。 ?(遷移強度),來控制從激活值遷移多少難度到權重值。一個合適的遷移強度值能夠讓權重和激活都易于量化。 \alpha 太大,權重難以量化, 太大,權重難以量化, ?太大,權重難以量化, \alpha $?太小激活難以量化。
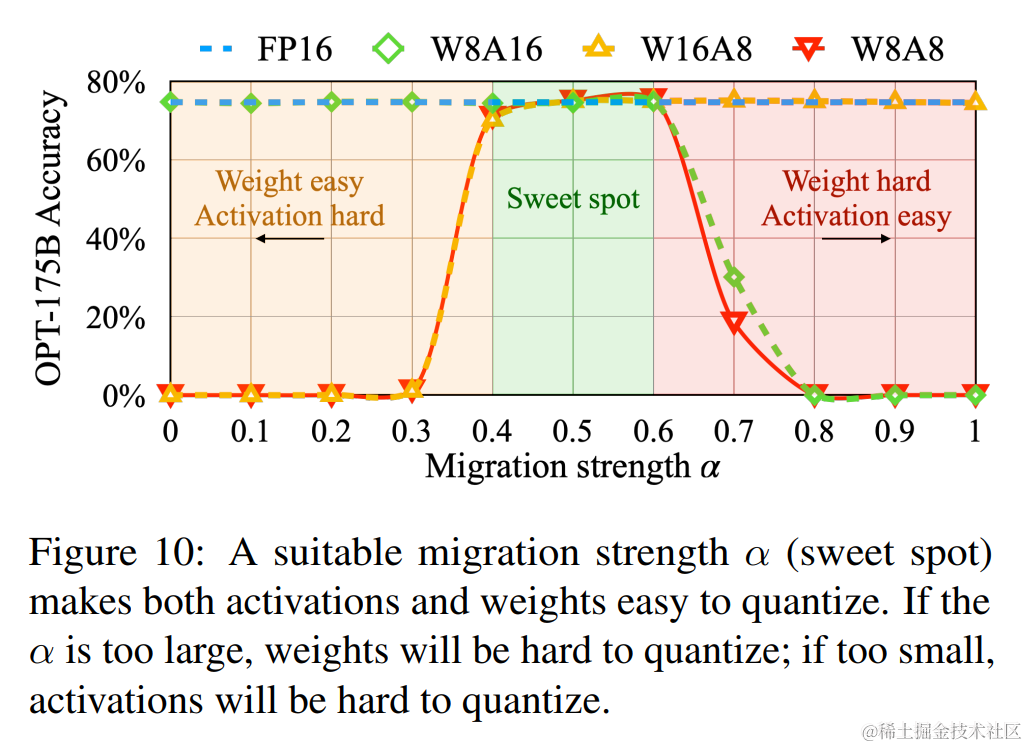
通過實驗發現,針對 OPT 和 BLOOM 模型,?$ \alpha = 0.5 是一個很好的平衡點;針對 G L M ? 130 B ,該模型有 30 =0.5?是一個很好的平衡點;針對 GLM-130B,該模型有 30%的異常值,激活值量化難度更大,可以選擇? =0.5?是一個很好的平衡點;針對GLM?130B,該模型有30 \alpha $=0.75?。
下圖展示了當 α 為 0.5 時 SmoothQuant 的主要思想。

平滑因子 s 是在校準樣本上獲得的,整個轉換是離線執行的。在運行時,激活是平滑的,無需縮放,具體步驟如下:
- 校準階段(離線)
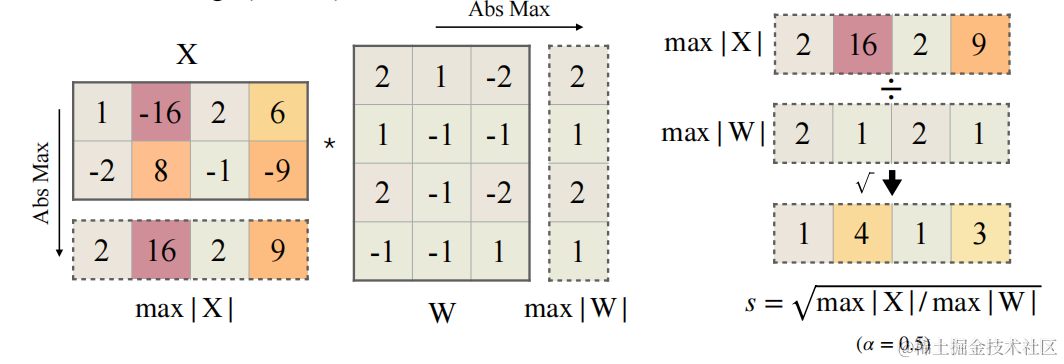
平滑因子s的計算公式如下:
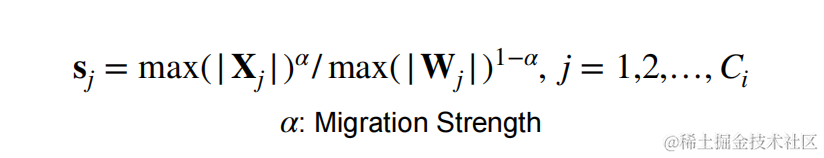
- $ \alpha $ 表示遷移強度,為一個超參數,控制將多少激活值的量化難度遷移到權重量化。
- C C C 表示激活的輸入通道數。
- 平滑階段(離線)
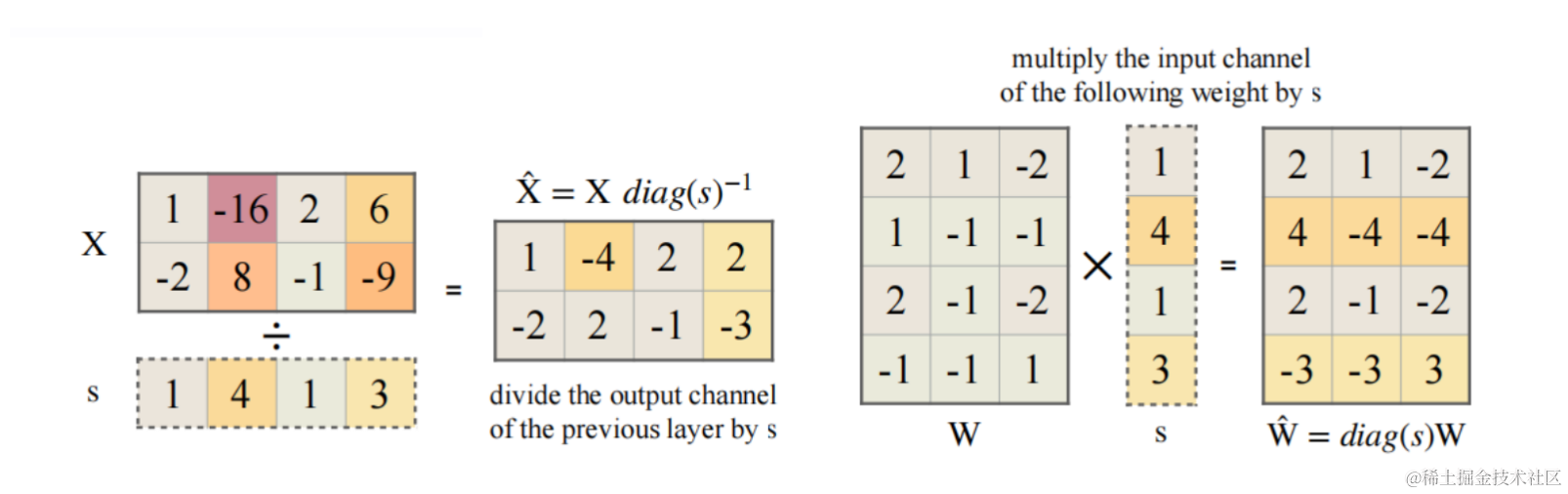
X ^ , W ^ \hat{X}, \hat{W} X^,W^ 的計算公式如下:
- $\hat{W}=diag(s) W $
- X ^ = X d i a g ( s ) ? 1 \hat{X}=X diag(s)^{-1} X^=Xdiag(s)?1
- 推理階段(在線,部署模型)
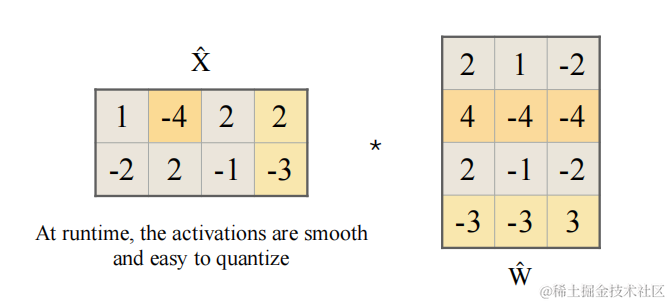
平滑之后的激活的計算公式如下:
Y = X ^ W ^ Y = \hat{X} \hat{W} Y=X^W^
將 SmoothQuant 應用于 Transformer 塊
在Transformer 塊中,將所有計算密集型算子(如:線性層、batched matmul (BMMs) )使用 INT8 運算,同時將其他輕量級算子(如:LayerNorm/Softmax)使用 FP16 運算 ,這樣可以均衡精度和推理效率。
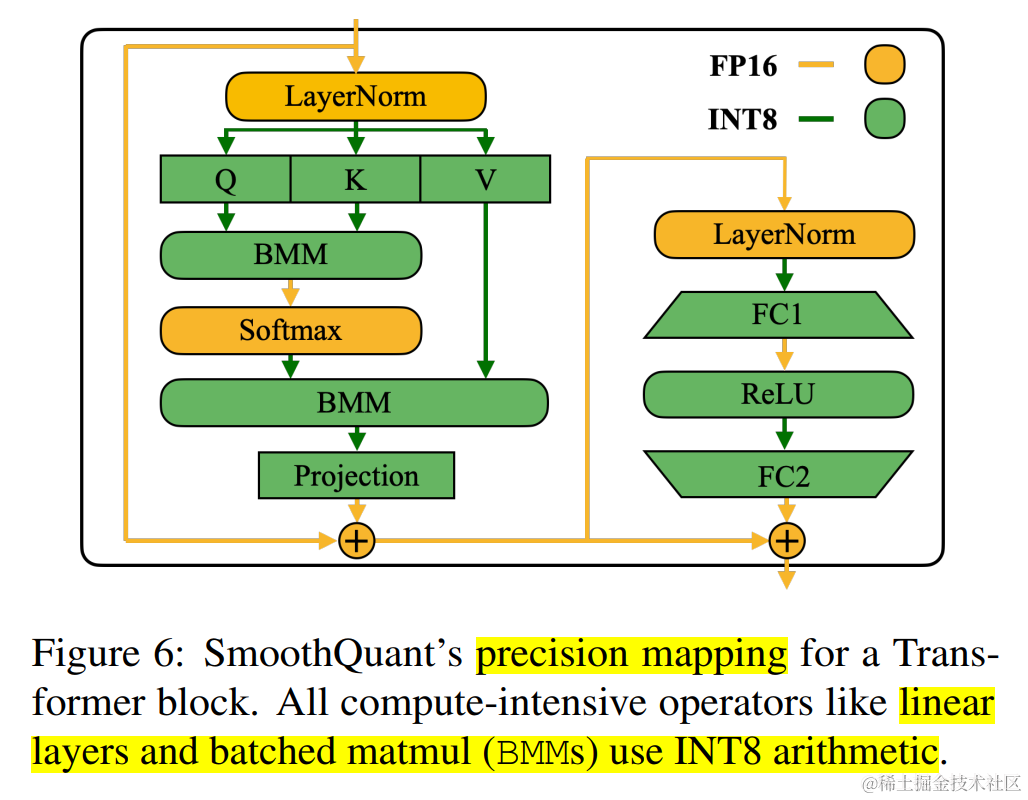
SmoothQuant 推理性能及精度
SmoothQuant可以無損地量化所有超過100B參數的開源LLM。
根據量化方式不同,作者提出三種策略 O1、O2、O3,其計算延遲依次降低。SmoothQuant的O1和O2級成功地保持了浮點精度,而O3級(per-tensor static)使平均精度下降了0.8%,可能是因為靜態收集的統計數據與真實評估樣本的激活統計數據之間的差異。

OPT-175B 使用 SmoothQuant 進行 int8 量化之后保持了與FP16相當的精度。
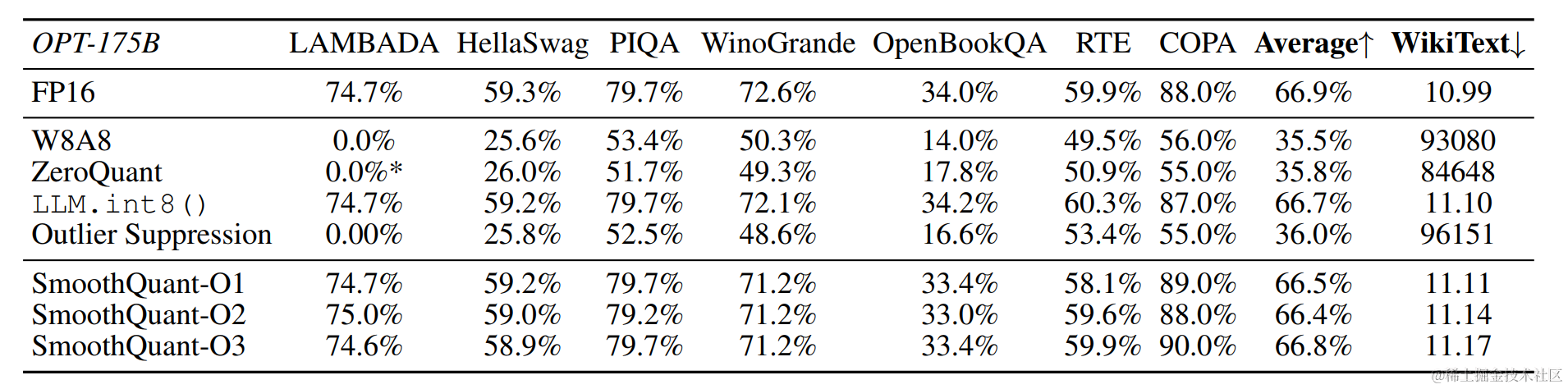
對于不同的LLM,SmoothQuant 相比其他量化方法(如:LLM.int8()、ZeroQuant等)具有更高的精度。
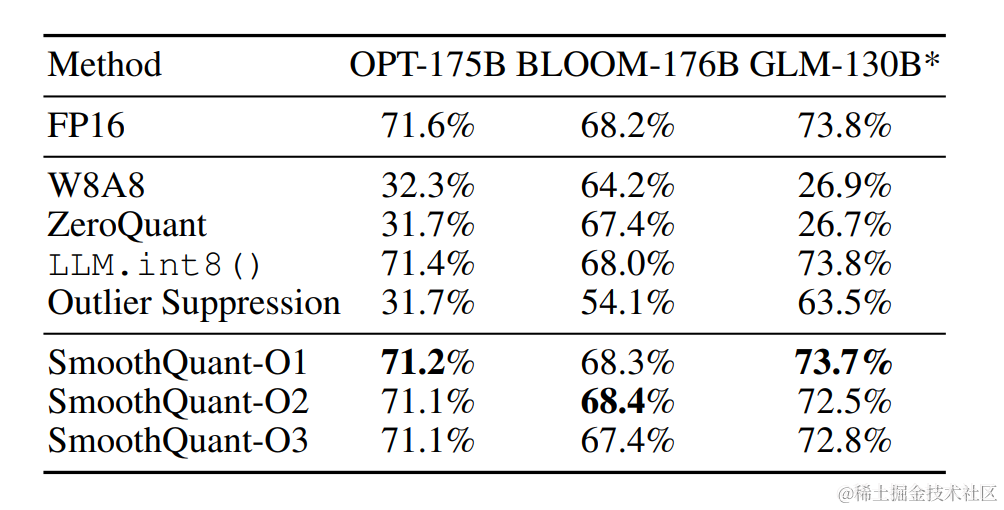
作者將SmoothQuant集成到PyTorch和FasterTransformer中,與 FP16 相比,獲得高達1.56倍的推理加速,并將內存占用減半,并且模型越大,加速效果越明顯。
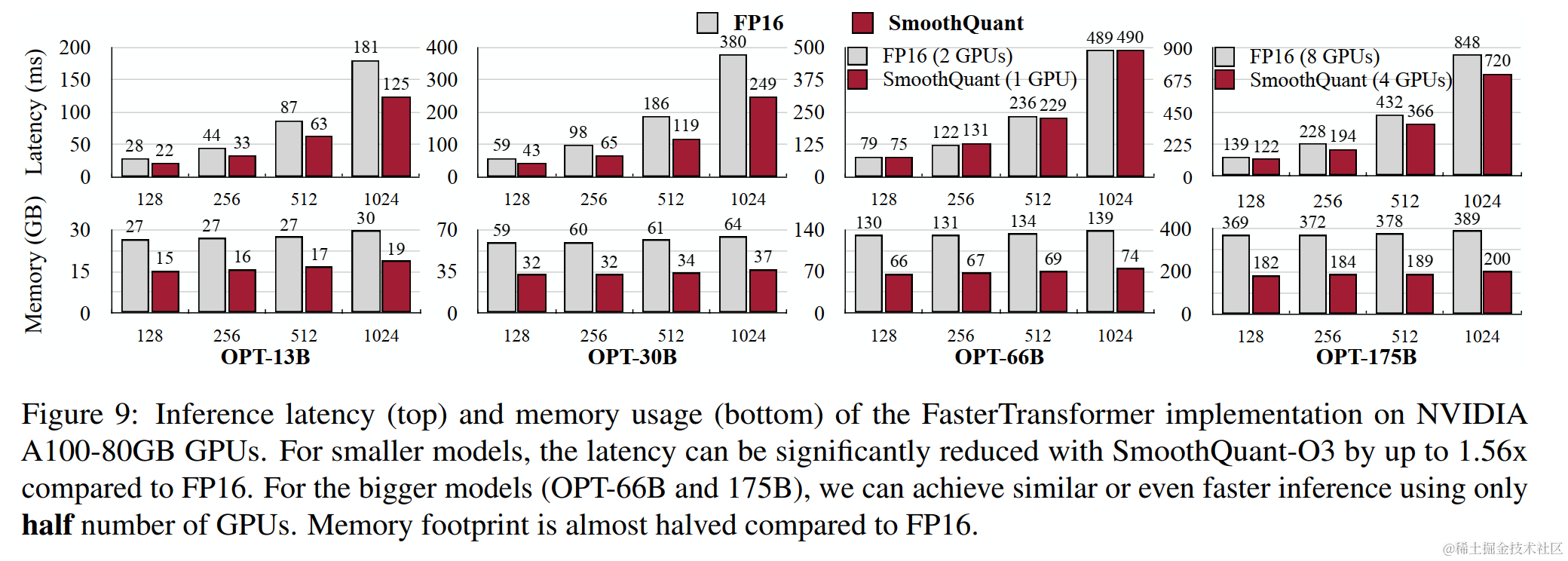
SmoothQuant 應用
官方示例:
- generate_act_scales.py:生成激活 scales
- export_int8_model.py:平滑、量化以及導出INT8模型
- smoothquant_opt_demo.ipynb:SmoothQuant 偽量化示例
- smoothquant_opt_real_int8_demo.ipynb:SmoothQuant 真正的量化示例
使用 FP16 模擬 8 比特動態 per- tensor 權重和激活量化,即偽量化。
import torch
from transformers.models.opt.modeling_opt import OPTAttention, OPTDecoderLayer, OPTForCausalLM
from smoothquant.smooth import smooth_lm
from smoothquant.fake_quant import W8A8Linear# 模型量化
def quantize_model(model, weight_quant='per_tensor', act_quant='per_tensor', quantize_bmm_input=True):for name, m in model.model.named_modules():if isinstance(m, OPTDecoderLayer):m.fc1 = W8A8Linear.from_float(m.fc1, weight_quant=weight_quant, act_quant=act_quant)m.fc2 = W8A8Linear.from_float(m.fc2, weight_quant=weight_quant, act_quant=act_quant)elif isinstance(m, OPTAttention):# Her we simulate quantizing BMM inputs by quantizing the output of q_proj, k_proj, v_projm.q_proj = W8A8Linear.from_float(m.q_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)m.k_proj = W8A8Linear.from_float(m.k_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)m.v_proj = W8A8Linear.from_float(m.v_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)m.out_proj = W8A8Linear.from_float(m.out_proj, weight_quant=weight_quant, act_quant=act_quant)return model# 原生 W8A8 模型量化
model_fp16 = OPTForCausalLM.from_pretrained('facebook/opt-13b', torch_dtype=torch.float16, device_map='auto')
model_w8a8 = quantize_model(model_fp16)
print(model_w8a8)# SmoothQuant W8A8 模型量化(偽量化)
model = OPTForCausalLM.from_pretrained('facebook/opt-13b', torch_dtype=torch.float16, device_map='auto')
# 激活scales
act_scales = torch.load('../act_scales/opt-13b.pt')
smooth_lm(model, act_scales, 0.5)
model_smoothquant_w8a8 = quantize_model(model)
print(model_smoothquant_w8a8)
作者使用 CUTLASS INT8 GEMM 內核為 PyTorch 實現 SmoothQuant 真正的 INT8 推理,這些內核被包裝為 torch-int 中的 PyTorch 模塊。加載SmoothQuant量化后的模型示例如下:
from smoothquant.opt import Int8OPTForCausalLMdef print_model_size(model):# https://discuss.pytorch.org/t/finding-model-size/130275param_size = 0for param in model.parameters():param_size += param.nelement() * param.element_size()buffer_size = 0for buffer in model.buffers():buffer_size += buffer.nelement() * buffer.element_size()size_all_mb = (param_size + buffer_size) / 1024**2print('Model size: {:.3f}MB'.format(size_all_mb))model_smoothquant = Int8OPTForCausalLM.from_pretrained('mit-han-lab/opt-30b-smoothquant', torch_dtype=torch.float16, device_map='auto')
print_model_size(model_smoothquant)
SmoothQuant 生態
目前,SmoothQuant 已經集成到了英偉達的 TensorRT-LLM 推理加速工具以及英特爾的 Neural-Compressor 模型壓縮工具包中。
總結
本文簡要介紹了誕生的SmoothQuant背景和技術原理,作者提到激活值比權重更難量化,因為權重數據分布一般比較均勻,而激活異常值多且大讓激活值量化變得更艱難,但是異常值只存在少數通道(Channel)內(單一 token 方差很大(異常值會存在于每一個 token 中),單一 channel 方差會小很多)。
因此,SmoothQuant 誕生。SmoothQuant 通過平滑激活層和權重后,再使用per-tensor或per-token量化,實現W8A8。根據量化方式不同,作者提出三種策略 O1、O2、O3,計算延遲依次降低。與其他量化方法相比,該方法可以保持較高的精度,同時,具有更低的延遲。
碼字不易,如果覺得我的文章能夠能夠給您帶來幫助,期待您的點贊收藏加關注~~
參考文檔
- https://github.com/mit-han-lab/smoothquant
- https://arxiv.org/pdf/2211.10438.pdf
- https://github.com/mit-han-lab/smoothquant/blob/main/assets/SmoothQuant.pdf
- https://blog.csdn.net/LoveJSH/article/details/132114469
- 大語言模型的模型量化(INT8/INT4):https://zhuanlan.zhihu.com/p/627436535
- SmoothQuant Real-INT8 Inference for PyTorch:https://github.com/mit-han-lab/smoothquant/blob/main/examples/smoothquant_opt_real_int8_demo.ipynb
- SmoothQuant on OPT-13B:https://github.com/mit-han-lab/smoothquant/blob/main/examples/smoothquant_opt_demo.ipynb
時序差分)


















3A5000虛擬機系統詳細教程)