時序差分（TD）是強化學習的核心，其是蒙特卡羅（MC）和動態規劃（DP）的結合。

1、TD 預測

TD 和 MC 都是利用經驗來解決預測問題。一種非平穩環境的一般訪問蒙特卡羅方法是
$$V(S_t)\leftarrow V(S_t)+\alpha \left[G_t?V(S_t)\right]$$

MC 方法必須等到事件結束才能確定 $V(S_t)$ 的增量（因為結束 $G_t$ 才是已知的），而 TD 方法只需要等到下一個時間步長。在時間 $t+1$ 時，立即生成一個目標，并使用觀察到的獎勵 $R_{t+1}$ 和估計值 $V(S_{t+1})$ 進行有用的更新，最簡單的 TD 方法更新方式如下：
$$V(S_t)\leftarrow V(S_t)+\alpha \left[R_{t+1}+\gamma V(S_{t+1})?V(S_t)\right]$$

MC 方法更新的目標是 $G_t$，而 TD 方法的目標是 $R_{t+1}+\gamma V(S_{t+1})$。這種 TD 方法稱為 $\mathrm{TD}(0)$。
$$\begin{array}{rl}{v}_{\pi }(s)& ?{\mathbb{E}}_{\pi }\left[G_t|S_t=s\right]\\ & ={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma G_{t+1}|S_t=s\right]\\ & ={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma v_{\pi }(S_{t+1})\right]\end{array}$$

由上式，MC 方法使用第二行的估計值作為目標，而 DP 方法使用第三行的估計值作為目標。MC 目標是一個估計值，因為期望值是未知的，我們是用平均樣本收益代替實際的期望收益；DP 目標也是一個估計值，雖然環境模型完全已知，但是 $v_{\pi }(S_{t+1})$ 是未知的，使用的當前的估計值；TD 目標也是一個估計值，因為它對第三行中的期望值進行采樣，且使用的當前的估計值而不是真實的 $v_{\pi }$。因此，TD 方法結合了 MC 的采樣和 DP 的自舉。

另外，$\mathrm{TD}(0)$ 算法中括號內是一種誤差，即狀態 $S_t$ 的當前估計值與更好的估計值 $R_{t+1}+\gamma V(S_{t+1})$ 的差異，這個量稱為 $\mathrm{TD}$ 誤差（$TDerror$），在強化學習中以各種形式出現：
$${\delta }_t?R_{t+1}+\gamma V(S_{t+1})?V(S_t)$$

2、TD 預測的優點

顯然，TD 方法比 DP 方法有一個優勢，因為它無需環境模型已知。TD 方法比 MC 方法的一個明顯的優勢是，它以在線、完全增量的方式實現；另外 MC 方法需要等到一個回合結束，而 TD 方法只需要等待一個時間步，這很關鍵，某些特殊情形可能回合結束時間太長，甚至回合不會結束。

3、TD(0) 的最優性

假設只有有限的經驗，例如 10 個回合或 100 個時間步長，在這種情況下，增量學習方法的常見手段是反復呈現經驗，直到收斂到一個值。給定一個近似價值函數 $V$，MC 增量和 TD 增量

4、Sarsa：同策略 TD 控制

現在我們使用 TD 預測方法來解決控制問題，與之前一樣，我們遵循廣義策略迭代（GPI）的模式，與 MC 方法一樣，我們面臨著進行探索的需要，同樣，方法分為兩大類：同策略和異策略。本節提出一種同策略上的 TD 控制方法。

第一步是學習動作價值函數而不是狀態價值函數，對于同策略方法，我們必須估計 $q_{\pi }(s,a),?s\in \mathcal{S},?a\in \mathcal{A}$，一個回合由狀態和狀態-動作對的交替序列組成：

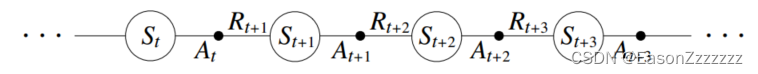
在前一章中，我們考慮從狀態到狀態的轉換，并學習了狀態的價值。現在我們考慮從狀態-動作對到狀態-動作對的轉換，并學習狀態-動作對的價值。形式上，這兩種情況是一樣的：它們都是帶有獎勵過程的馬爾可夫鏈，保證 $\mathrm{TD}(0)$ 下狀態價值收斂的定理也適用于動作價值的相應算法：
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_{t+1}+\gamma Q(S_{t+1},A_{t+1})?Q(S_t,A_t)\right]$$

5、Q-learning：異策略 TD 控制

強化學習的早期突破之一就是開發了一種被稱為 Q-learning 的異策略 TD 控制算法，定義如下
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a)?Q(S_t,A_t)\right]$$