代碼隨想錄 二叉樹第二周

目錄

101.對稱二叉樹

100.相同的樹

572.另一棵樹的子樹

104.二叉樹的最大深度

559.N叉樹的最大深度

?111.二叉樹的最小深度

222.完全二叉樹的節點個數

110.平衡二叉樹?

257.二叉樹的所有路徑

101.對稱二叉樹

101. 對稱二叉樹

已解答

簡單

相關標簽

相關企業

給你一個二叉樹的根節點?root?， 檢查它是否軸對稱。

示例 1：

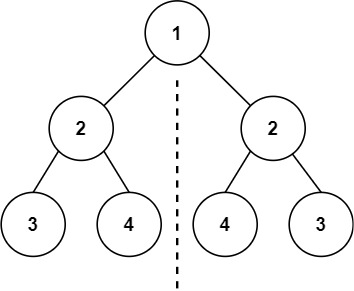
輸入：root = [1,2,2,3,4,4,3]
輸出：true

示例 2：

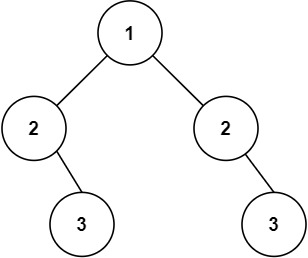
輸入：root = [1,2,2,null,3,null,3]
輸出：false

提示：

  • 樹中節點數目在范圍?[1, 1000]?內
  • -100 <= Node.val <= 100

進階：你可以運用遞歸和迭代兩種方法解決這個問題嗎？

這個整體的思路是去比較該節點的左右子樹是否可以翻轉，判斷左右節點的值后，比較左節點的左子樹與右節點的右子樹，以及左節點的右子樹與右節點的左子樹是否對稱

遞歸法：

/*** Definition for a binary tree node.* 二叉樹節點的定義* public class TreeNode {*     int val; // 節點值*     TreeNode left; // 左子節點*     TreeNode right; // 右子節點*     TreeNode() {} // 構造函數*     TreeNode(int val) { this.val = val; } // 帶值的構造函數*     TreeNode(int val, TreeNode left, TreeNode right) { // 帶值和子節點的構造函數*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 判斷是否對稱函數public boolean isSymmetric(TreeNode root) {// 調用遞歸函數比較左右子樹return compare(root.left, root.right);}// 遞歸比較左右子樹是否對稱public boolean compare(TreeNode left, TreeNode right) {// 如果左右子節點都為空，則對稱if (left == null && right == null) {return true;}// 如果左右子節點其中一個為空，另一個不為空，則不對稱if (left == null || right == null) {return false;}// 如果左右子節點的值不相等，則不對稱if (left.val != right.val) {return false;}// 遞歸比較左子節點的左子樹與右子節點的右子樹，以及左子節點的右子樹與右子節點的左子樹是否對稱boolean out = compare(left.left, right.right);boolean in = compare(left.right, right.left);// 如果左右子樹都對稱，則整體對稱return out && in;}
}

迭代法：

/*** 迭代法* 使用雙端隊列，相當于兩個棧*/public boolean isSymmetric2(TreeNode root) {Deque<TreeNode> deque = new LinkedList<>();deque.offerFirst(root.left);deque.offerLast(root.right);while (!deque.isEmpty()) {TreeNode leftNode = deque.pollFirst();TreeNode rightNode = deque.pollLast();if (leftNode == null && rightNode == null) {continue;}
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }// 以上三個判斷條件合并if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {return false;}deque.offerFirst(leftNode.left);deque.offerFirst(leftNode.right);deque.offerLast(rightNode.right);deque.offerLast(rightNode.left);}return true;}/*** 迭代法* 使用普通隊列*/public boolean isSymmetric3(TreeNode root) {Queue<TreeNode> deque = new LinkedList<>();deque.offer(root.left);deque.offer(root.right);while (!deque.isEmpty()) {TreeNode leftNode = deque.poll();TreeNode rightNode = deque.poll();if (leftNode == null && rightNode == null) {continue;}
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }// 以上三個判斷條件合并if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {return false;}// 這里順序與使用Deque不同deque.offer(leftNode.left);deque.offer(rightNode.right);deque.offer(leftNode.right);deque.offer(rightNode.left);}return true;}

100.相同的樹

100. 相同的樹

已解答

簡單

相關標簽

相關企業

給你兩棵二叉樹的根節點?p?和?q?，編寫一個函數來檢驗這兩棵樹是否相同。

如果兩個樹在結構上相同，并且節點具有相同的值，則認為它們是相同的。

示例 1：

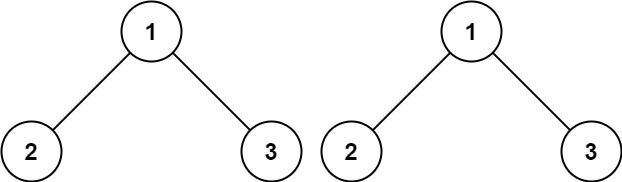
輸入：p = [1,2,3], q = [1,2,3]
輸出：true

示例 2：

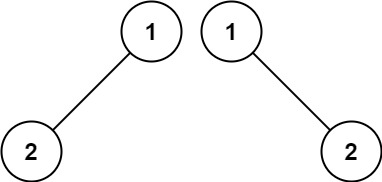
輸入：p = [1,2], q = [1,null,2]
輸出：false

示例 3：

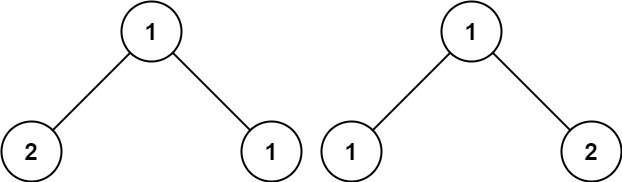
輸入：p = [1,2,1], q = [1,1,2]
輸出：false

提示：

  • 兩棵樹上的節點數目都在范圍?[0, 100]?內
  • -104 <= Node.val <= 104
/*** Definition for a binary tree node.* 二叉樹節點的定義* public class TreeNode {*     int val; // 節點值*     TreeNode left; // 左子節點*     TreeNode right; // 右子節點*     TreeNode() {} // 空構造函數*     TreeNode(int val) { this.val = val; } // 帶值的構造函數*     TreeNode(int val, TreeNode left, TreeNode right) { // 帶值和子節點的構造函數*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 判斷是否相同樹的函數public boolean isSameTree(TreeNode p, TreeNode q) {// 如果左右子節點都為空，則相同if (p == null && q == null) {return true;}// 如果左右子節點其中一個為空，另一個不為空，則不相同if (p == null || q == null) {return false;}// 如果左右子節點的值不相等，則不相同if (p.val != q.val) {return false;}// 遞歸比較左子節點的左子樹與右子節點的右子樹，以及左子節點的右子樹與右子節點的左子樹是否相同boolean left = isSameTree(p.left, q.left);boolean right = isSameTree(p.right, q.right);// 如果左右子樹都相同，則整體相同return left && right;}
}

572.另一棵樹的子樹

572. 另一棵樹的子樹

已解答

簡單

相關標簽

相關企業

提示

給你兩棵二叉樹?root?和?subRoot?。檢驗?root?中是否包含和?subRoot?具有相同結構和節點值的子樹。如果存在，返回?true?；否則，返回?false?。

二叉樹?tree?的一棵子樹包括?tree?的某個節點和這個節點的所有后代節點。tree?也可以看做它自身的一棵子樹。

示例 1：

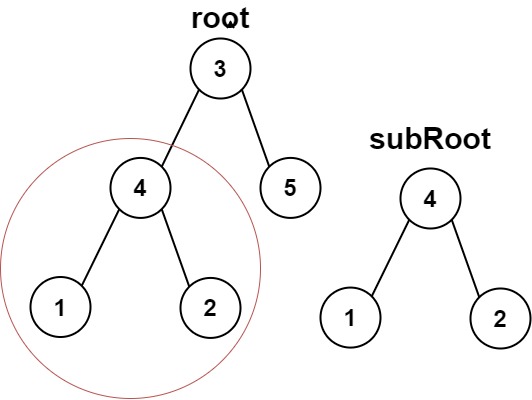
輸入：root = [3,4,5,1,2], subRoot = [4,1,2]
輸出：true

示例 2：

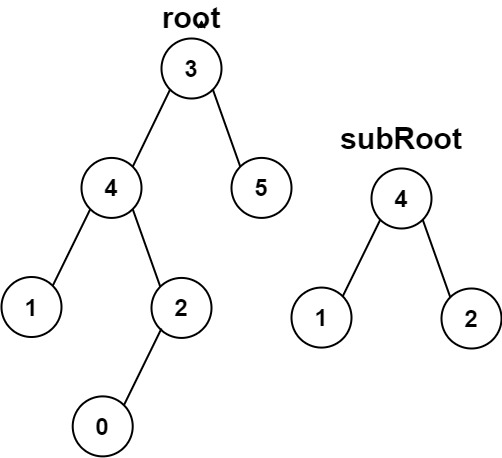
輸入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
輸出：false

提示：

  • root?樹上的節點數量范圍是?[1, 2000]
  • subRoot?樹上的節點數量范圍是?[1, 1000]
  • -104 <= root.val <= 104
  • -104 <= subRoot.val <= 104
/*** Definition for a binary tree node.* 二叉樹節點的定義* public class TreeNode {*     int val; // 節點值*     TreeNode left; // 左子節點*     TreeNode right; // 右子節點*     TreeNode() {} // 空構造函數*     TreeNode(int val) { this.val = val; } // 帶值的構造函數*     TreeNode(int val, TreeNode left, TreeNode right) { // 帶值和子節點的構造函數*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 判斷是否子樹的函數public boolean isSubtree(TreeNode root, TreeNode subRoot) {// 如果根節點為空，則返回falseif (root == null) {return false;}// 判斷當前子樹是否與給定子樹相同，或者在左子樹或右子樹中是否存在相同子樹return isSameTree(root, subRoot) || isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);}// 判斷是否相同樹的函數public boolean isSameTree(TreeNode p, TreeNode q) {// 如果左右子節點都為空，則相同if (p == null && q == null) {return true;}// 如果左右子節點其中一個為空，另一個不為空，則不相同if (p == null || q == null) {return false;}// 如果左右子節點的值不相等，則不相同if (p.val != q.val) {return false;}// 遞歸比較左子節點的左子樹與右子節點的右子樹，以及左子節點的右子樹與右子節點的左子樹是否相同boolean left = isSameTree(p.left, q.left);boolean right = isSameTree(p.right, q.right);// 如果左右子樹都相同，則整體相同return left && right;}
}

104.二叉樹的最大深度

104. 二叉樹的最大深度

簡單

給定一個二叉樹?root?，返回其最大深度。

二叉樹的?最大深度?是指從根節點到最遠葉子節點的最長路徑上的節點數。

示例 1：

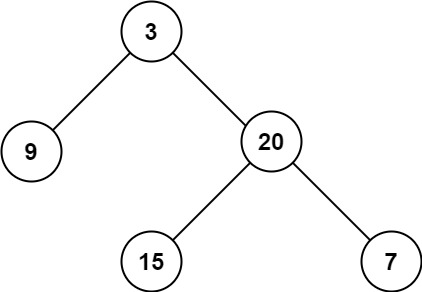
輸入：root = [3,9,20,null,null,15,7]
輸出：3

示例 2：

輸入：root = [1,null,2]
輸出：2

提示：

  • 樹中節點的數量在?[0, 104]?區間內。
  • -100 <= Node.val <= 100

廣度優先遍歷

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int maxDepth(TreeNode root) {// 如果根節點為空，直接返回深度為0if (root == null) {return 0;}// 創建一個隊列用于輔助層序遍歷Queue<TreeNode> queue = new LinkedList<>();// 將根節點加入隊列queue.offer(root);int depth = 0;// 當隊列不為空時，繼續遍歷while (!queue.isEmpty()) {// 記錄當前層的節點數int size = queue.size();// 遍歷當前層的所有節點while (size-- > 0) {// 從隊列中取出一個節點TreeNode node = queue.poll();// 將當前節點的左子節點加入隊列（如果存在）if (node.left != null) {queue.offer(node.left);}// 將當前節點的右子節點加入隊列（如果存在）if (node.right != null) {queue.offer(node.right);}}depth++; // 深度加1}// 返回樹的最大深度return depth;}
}

深度優先遍歷

求深度可看做是求高度，通過遞歸的方式，結束條件是節點為空，返回高度為0，每一個節點求出子樹高度的最大值加一為該節點的高度，根節點的高度即為二叉樹的最大深度

/*** Definition for a binary tree node.* 二叉樹節點的定義* public class TreeNode {*     int val; // 節點值*     TreeNode left; // 左子節點*     TreeNode right; // 右子節點*     TreeNode() {} // 空構造函數*     TreeNode(int val) { this.val = val; } // 帶值的構造函數*     TreeNode(int val, TreeNode left, TreeNode right) { // 帶值和子節點的構造函數*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 計算二叉樹的最大深度函數public int maxDepth(TreeNode root) {// 如果根節點為空，樹的深度為0if (root == null) {return 0;}// 分別計算左右子樹的深度int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);// 取左右子樹深度的最大值，并加上根節點的深度1，得到整棵樹的深度int height = Math.max(leftHeight, rightHeight) + 1;return height;}
}

559.N叉樹的最大深度

559. N 叉樹的最大深度

簡單

給定一個 N 叉樹，找到其最大深度。

最大深度是指從根節點到最遠葉子節點的最長路徑上的節點總數。

N 叉樹輸入按層序遍歷序列化表示，每組子節點由空值分隔（請參見示例）。

示例 1：

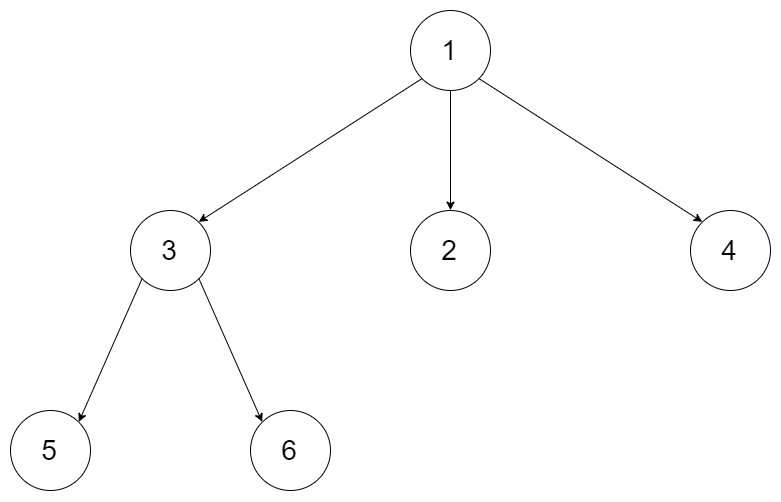
輸入：root = [1,null,3,2,4,null,5,6]
輸出：3

示例 2：

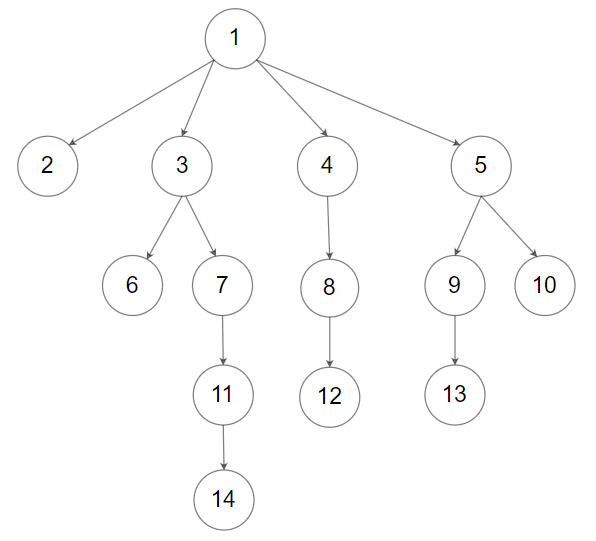
輸入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
輸出：5

提示：

  • 樹的深度不會超過?1000?。
  • 樹的節點數目位于?[0,?104]?之間。

深度優先遍歷

/*
// Definition for a Node.
// 節點類的定義
class Node {public int val; // 節點值public List<Node> children; // 子節點列表// 構造函數public Node() {}// 帶值的構造函數public Node(int _val) {val = _val;}// 帶值和子節點列表的構造函數public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {// 計算多叉樹的最大深度函數public int maxDepth(Node root) {// 初始化最大深度為0int max = 0;// 如果根節點為空，返回0if (root == null) {return 0;}// 遍歷子節點列表for (Node child : root.children) {// 遞歸計算子節點的最大深度，并更新最大值max = Math.max(max, maxDepth(child));}// 返回最大深度加上當前節點的深度1return max + 1;}
}

廣度優先遍歷

/*
// Definition for a Node.
// 節點類的定義
class Node {public int val; // 節點值public List<Node> children; // 子節點列表// 構造函數public Node() {}// 帶值的構造函數public Node(int _val) {val = _val;}// 帶值和子節點列表的構造函數public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {// 計算多叉樹的最大深度函數public int maxDepth(Node root) {// 如果根節點為空，直接返回深度為0if (root == null) {return 0;}// 創建一個隊列用于輔助層序遍歷Queue<Node> queue = new LinkedList<>();// 將根節點加入隊列queue.offer(root);int depth = 0;// 當隊列不為空時，繼續遍歷while (!queue.isEmpty()) {// 記錄當前層的節點數int size = queue.size();// 遍歷當前層的所有節點while (size-- > 0) {// 從隊列中取出一個節點Node node = queue.poll();// 將當前節點的子節點加入隊列if (!node.children.isEmpty()) {for (Node child : node.children) {queue.offer(child);}}}depth++; // 深度加1}// 返回樹的最大深度return depth;}
}

?111.二叉樹的最小深度

111. 二叉樹的最小深度

簡單

給定一個二叉樹，找出其最小深度。

最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。

說明：葉子節點是指沒有子節點的節點。

示例 1：

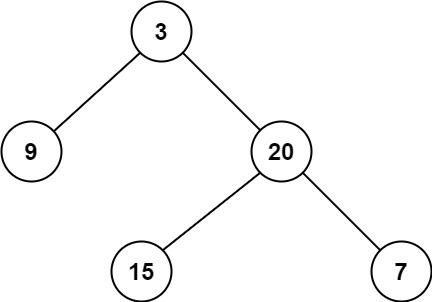
輸入：root = [3,9,20,null,null,15,7]
輸出：2

示例 2：

輸入：root = [2,null,3,null,4,null,5,null,6]
輸出：5

提示：

  • 樹中節點數的范圍在?[0, 105]?內
  • -1000 <= Node.val <= 1000

廣度優先遍歷?

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int minDepth(TreeNode root) {// 如果根節點為空，直接返回深度為0if (root == null) {return 0;}// 創建一個隊列用于輔助層序遍歷Queue<TreeNode> queue = new LinkedList<>();// 將根節點加入隊列queue.offer(root);int depth = 1;// 當隊列不為空時，繼續遍歷while (!queue.isEmpty()) {// 記錄當前層的節點數int size = queue.size();// 遍歷當前層的所有節點while (size-- > 0) {// 從隊列中取出一個節點TreeNode node = queue.poll();//如果當前節點的左右孩子都為空，直接返回最小深度if (node.left == null && node.right == null){return depth;}// 將當前節點的左子節點加入隊列（如果存在）if (node.left != null) {queue.offer(node.left);}// 將當前節點的右子節點加入隊列（如果存在）if (node.right != null) {queue.offer(node.right);}}depth++; // 深度加1}// 返回樹的深度return depth;}
}

深度優先遍歷?

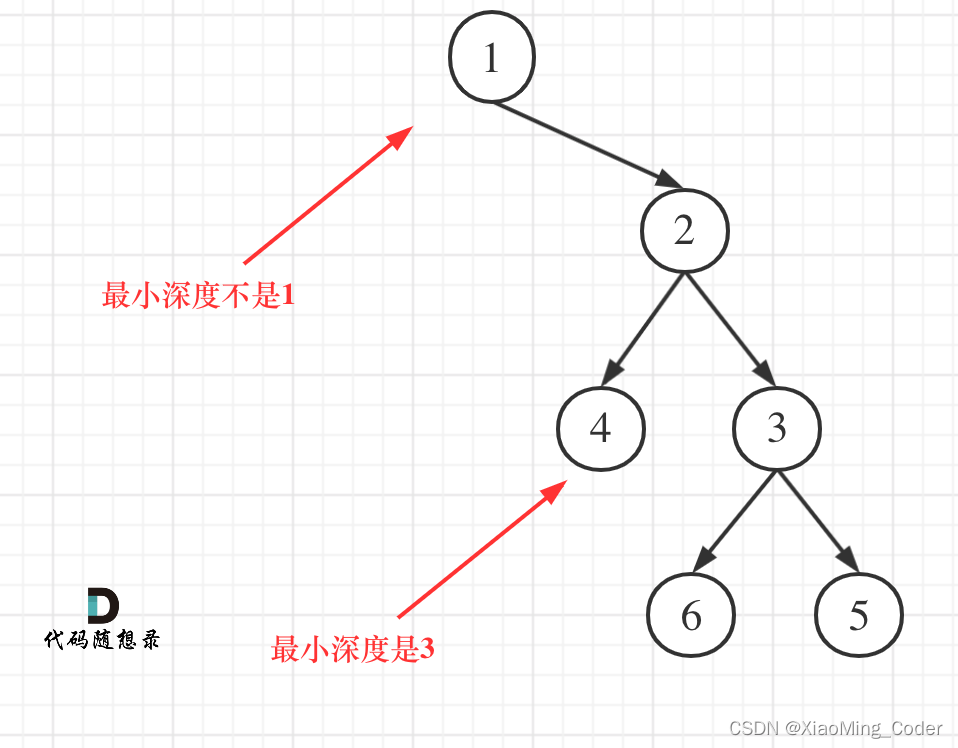
這里的深度優先遍歷與求二叉樹的最大深度有不同的地方，要著重明白最小深度是指葉節點到根節點的距離

采用和求二叉樹最大深度的求法的話，會導致出現如下情況

故要對左子樹為空或者右子樹為空的情況單獨判斷

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {/*** 計算二叉樹的最小深度*/public int minDepth(TreeNode root) {// 如果根節點為空，返回深度為0if (root == null) {return 0;}// 計算左子樹的最小深度int leftHeight = minDepth(root.left);// 計算右子樹的最小深度int rightHeight = minDepth(root.right);// 如果左子樹為空而右子樹不為空，返回右子樹的最小深度加上根節點深度if (root.left == null && root.right != null) {return rightHeight + 1;}// 如果右子樹為空而左子樹不為空，返回左子樹的最小深度加上根節點深度if (root.left != null && root.right == null) {return leftHeight + 1;}// 返回左右子樹最小深度的較小值加上根節點深度int result = Math.min(leftHeight, rightHeight) + 1;return result;}
}

222.完全二叉樹的節點個數

222. 完全二叉樹的節點個數

簡單

給你一棵?完全二叉樹?的根節點?root?，求出該樹的節點個數。

完全二叉樹?的定義如下：在完全二叉樹中，除了最底層節點可能沒填滿外，其余每層節點數都達到最大值，并且最下面一層的節點都集中在該層最左邊的若干位置。若最底層為第?h?層，則該層包含?1~?2h?個節點。

示例 1：

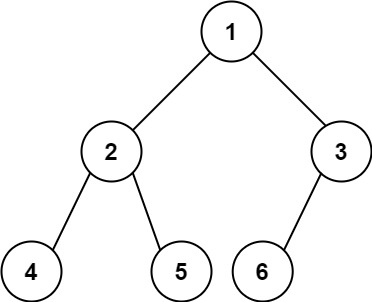
輸入：root = [1,2,3,4,5,6]
輸出：6

示例 2：

輸入：root = []
輸出：0

示例 3：

輸入：root = [1]
輸出：1

提示：

  • 樹中節點的數目范圍是[0, 5 * 104]
  • 0 <= Node.val <= 5 * 104
  • 題目數據保證輸入的樹是?完全二叉樹

進階：遍歷樹來統計節點是一種時間復雜度為?O(n)?的簡單解決方案。你可以設計一個更快的算法嗎？

利用完全二叉樹的性質。逐層找出完美二叉樹，通過公式求出節點個數返回

/*** 二叉樹節點的定義*/
class TreeNode {int val; // 節點值TreeNode left; // 左子節點TreeNode right; // 右子節點// 構造函數TreeNode() {}// 帶值的構造函數TreeNode(int val) {this.val = val;}// 帶值和子節點的構造函數TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {/*** 計算二叉樹的節點數*/public int countNodes(TreeNode root) {// 如果根節點為空，返回0if (root == null) {return 0;}// 初始化左子樹和右子樹的高度為0，并找到最左邊和最右邊的葉節點int leftHeight = 0;int rightHeight = 0;TreeNode turnLeft = root;while (turnLeft != null) {turnLeft = turnLeft.left;leftHeight++;}TreeNode turnRight = root;while (turnRight != null) {turnRight = turnRight.right;rightHeight++;}// 如果左右子樹高度相等，說明是滿二叉樹，直接返回節點數if (leftHeight == rightHeight) {return (2 << (leftHeight - 1)) - 1; // 注意(2<<1) 相當于2^2，所以leftHeight要減一}// 如果左右子樹高度不相等，分別計算左右子樹的節點數int leftCount = countNodes(root.left);int rightCount = countNodes(root.right);// 返回左右子樹節點數加上當前節點return leftCount + rightCount + 1;}
}

110.平衡二叉樹?

110. 平衡二叉樹

簡單

給定一個二叉樹，判斷它是否是高度平衡的二叉樹。

本題中，一棵高度平衡二叉樹定義為：

一個二叉樹每個節點?的左右兩個子樹的高度差的絕對值不超過 1 。

示例 1：

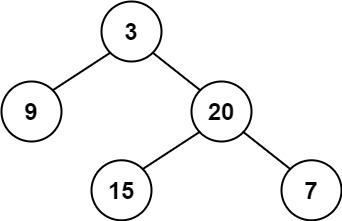
輸入：root = [3,9,20,null,null,15,7]
輸出：true

示例 2：

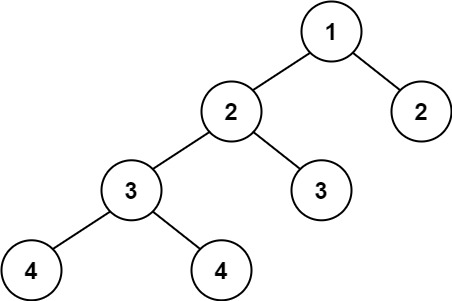
輸入：root = [1,2,2,3,3,null,null,4,4]
輸出：false

示例 3：

輸入：root = []
輸出：true

提示：

  • 樹中的節點數在范圍?[0, 5000]?內
  • -104 <= Node.val <= 104

深度優先遍歷?

計算左右子樹的高度，判斷左右子樹的高度差是否大于一

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {/*** 判斷二叉樹是否平衡*/public boolean isBalanced(TreeNode root) {// 如果平衡函數返回-1，說明不平衡if (balanced(root) == -1) {return false;}// 否則說明平衡return true;}/*** 計算二叉樹的高度，如果不平衡則返回-1*/public int balanced(TreeNode root) {// 如果節點為空，高度為0if (root == null) {return 0;}// 計算左子樹的高度int leftHeight = balanced(root.left);// 如果左子樹不平衡，直接返回-1if (leftHeight == -1) {return -1;}// 計算右子樹的高度int rightHeight = balanced(root.right);// 如果右子樹不平衡，直接返回-1if (rightHeight == -1) {return -1;}// 如果左右子樹高度差超過1，說明不平衡，返回-1if (Math.abs(leftHeight - rightHeight) > 1) {return -1;}// 返回左右子樹中較大的高度加上當前節點的高度return Math.max(leftHeight, rightHeight) + 1;}
}

廣度優先遍歷

計算每個節點的高度，通過迭代遍歷判斷左右子樹的高度差是否大于一

class Solution {/*** 迭代法，效率較低，計算高度時會重復遍歷* 時間復雜度：O(n^2)*/public boolean isBalanced(TreeNode root) {if (root == null) {return true;}Stack<TreeNode> stack = new Stack<>();TreeNode pre = null;while (root!= null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;}TreeNode inNode = stack.peek();// 右結點為null或已經遍歷過if (inNode.right == null || inNode.right == pre) {// 比較左右子樹的高度差，輸出if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {return false;}stack.pop();pre = inNode;root = null;// 當前結點下，沒有要遍歷的結點了} else {root = inNode.right;// 右結點還沒遍歷，遍歷右結點}}return true;}/*** 層序遍歷，求結點的高度*/public int getHeight(TreeNode root) {if (root == null) {return 0;}Deque<TreeNode> deque = new LinkedList<>();deque.offer(root);int depth = 0;while (!deque.isEmpty()) {int size = deque.size();depth++;for (int i = 0; i < size; i++) {TreeNode poll = deque.poll();if (poll.left != null) {deque.offer(poll.left);}if (poll.right != null) {deque.offer(poll.right);}}}return depth;}
}

257.二叉樹的所有路徑

257. 二叉樹的所有路徑

簡單

給你一個二叉樹的根節點?root?，按?任意順序?，返回所有從根節點到葉子節點的路徑。

葉子節點?是指沒有子節點的節點。

示例 1：

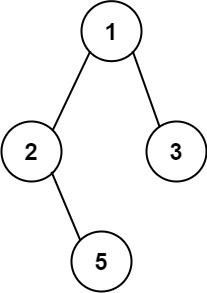
輸入：root = [1,2,3,null,5]
輸出：["1->2->5","1->3"]

示例 2：

輸入：root = [1]
輸出：["1"]

提示：

  • 樹中節點的數目在范圍?[1, 100]?內
  • -100 <= Node.val <= 100

迭代法

節點為空時直接返回，遞到葉子節點時將路徑存入結果集合中，沒遞到葉子節點的話，將現有的路徑傳入去訪問左右子節點。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {/*** 返回二叉樹所有從根到葉子的路徑*/public List<String> binaryTreePaths(TreeNode root) {List<String> result = new ArrayList<>();path(root, "", result);return result;}/*** 輔助函數，遞歸遍歷二叉樹并構建路徑*/public void path(TreeNode root, String path, List<String> result) {// 如果節點為空，直接返回if (root == null) {return;}// 構建當前路徑的字符串表示StringBuilder pathSB = new StringBuilder(path);pathSB.append(Integer.toString(root.val));// 如果當前節點是葉子節點，將路徑加入結果列表if (root.left == null && root.right == null) {result.add(pathSB.toString());} else {// 否則，繼續遞歸遍歷左右子樹pathSB.append("->"); // 添加箭頭分隔符path(root.left, pathSB.toString(), result);path(root.right, pathSB.toString(), result);}}
}

?層序遍歷

通過一個棧，節點和路徑同時入棧和出棧，同樣到葉子節點的話將路徑傳入結果集合中

class Solution {/*** 迭代法*/public List<String> binaryTreePaths(TreeNode root) {List<String> result = new ArrayList<>();if (root == null)return result;Stack<Object> stack = new Stack<>();// 節點和路徑同時入棧stack.push(root);stack.push(root.val + "");while (!stack.isEmpty()) {// 節點和路徑同時出棧String path = (String) stack.pop();TreeNode node = (TreeNode) stack.pop();// 若找到葉子節點if (node.left == null && node.right == null) {result.add(path);}//右子節點不為空if (node.right != null) {stack.push(node.right);stack.push(path + "->" + node.right.val);}//左子節點不為空if (node.left != null) {stack.push(node.left);stack.push(path + "->" + node.left.val);}}return result;}
}


?

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/711989.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/711989.shtml
英文地址，請注明出處：http://en.pswp.cn/news/711989.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

《求生之路2》服務器如何選擇合適的內存和CPU核心數，以避免丟包和延遲高？

《求生之路2》服務器如何選擇合適的內存和CPU核心數，以避免丟包和延遲高？

根據求生之路2服務器的實際案例分析選擇合適的內存和CPU核心數以避免丟包和延遲高的問題&#xff0c;首先需要考慮游戲的類型和對服務器配置的具體要求。《求生之路2》作為一款多人在線射擊游戲&#xff0c;其服務器和網絡優化對于玩家體驗至關重要。 首先&#xff0c;考慮到游…
閱讀更多...
Java應用程序注冊成Linux系統服務后，關閉Java應用程序打印系統日志

Java應用程序注冊成Linux系統服務后，關閉Java應用程序打印系統日志

Java應用程序有自己的日志框架&#xff0c;有指定位置的日志文件&#xff0c;不需要在系統日志里記錄&#xff0c;占用磁盤空間。 1.Linux系統文件目錄 /etc/systemd/system/ 找到要修改的Java應用程序服務配置 比如bis-wz-80.service 2.設置不打印日志 StandardOutputnull S…
閱讀更多...
centos7 搭建 harbor 私有倉庫

centos7 搭建 harbor 私有倉庫

一、下載安裝 1.1、harbor 可以直接從 github 上下載&#xff1a;Releases goharbor/harbor GitHub 這里選擇 v2.10.0 的版本 wget https://github.com/goharbor/harbor/releases/download/v2.10.0/harbor-offline-installer-v2.10.0.tgz 1.2、解壓 tar zxvf harbor-offlin…
閱讀更多...
L2 網絡 Mint Blockchain 正式對外發布測試網

L2 網絡 Mint Blockchain 正式對外發布測試網

Mint Blockchain 是由 NFTScan Labs 發起的聚焦在 NFT 生態的 L2 網絡&#xff0c;致力于促進 NFT 資產協議標準的創新和 NFT 在現實商業應用場景中的大規模采用。 Mint Blockchain 于 2024 年 2 月 28 號正式對外發布測試網&#xff0c;開始全面進入生態開發者測試開發階段。 …
閱讀更多...
2403C++,C++11玩轉無棧協程

2403C++,C++11玩轉無棧協程

原文 C11里也能玩無棧協程了? 答案是:可以! 事實上異網在很早時,C11里就可用無棧協程寫異步代碼了,只不過用起來不太方便,來看看C11里怎么用異網無棧協程寫一個回音服務器的吧. #包含 <異網.h> #包含 <內存> #包含 <向量> #包含 <異網/產生.h> 用 …
閱讀更多...
c++異常機制（5）-- 繼承與異常

c++異常機制（5）-- 繼承與異常

我們在c異常機制(3)中自定義類型&#xff0c;我們將相應的異常封裝成了類&#xff0c;在類中實現一些方法&#xff0c;對異常進行處理。其中每一個類都實現了print()方法。 我們使用throw拋出相應異常的虛擬對象&#xff0c;在catch參數中進行匹配&#xff0c;但是如果有很多異…
閱讀更多...
Springboot項目集成短信驗證碼（超簡單）

Springboot項目集成短信驗證碼（超簡單）

操作流程 注冊驗證碼平臺創建驗證碼模版開始集成&#xff08;無需引入第三方庫&#xff09; 注冊并登陸中昱維信驗證碼平臺 獲取AppID和AppKey。 創建驗證碼模版 創建驗證碼模版&#xff0c;獲取驗證碼模版id 開始集成 創建controller import org.springframework.web.bi…
閱讀更多...
MATLAB環境下基于隨機游走拉普拉斯算子的快速譜聚類方法

MATLAB環境下基于隨機游走拉普拉斯算子的快速譜聚類方法

古人有云&#xff0c;物以類聚&#xff0c;在面臨信息爆炸問題的今天&#xff0c;對信息類別劃分的價值日益顯現&#xff0c;并逐步成為學者們的研究熱點。分類和聚類是數據挖掘的重要工具&#xff0c;是實現事物類別劃分的左右手&#xff0c;聚類又是分類一種特殊的方式。所謂…
閱讀更多...
CodeWhisperer安裝教導--一步到位！以及本人使用Whisperer的初體驗。

CodeWhisperer安裝教導--一步到位！以及本人使用Whisperer的初體驗。

CodeWhisperer是亞馬遜出品的一款基于機器學習的通用代碼生成器&#xff0c;可實時提供代碼建議。類似 Cursor 和Github AWS CodeWhisperer 亞馬遜科技的CodeWhisperer是Amazon于2021年12月推出的一款代碼補全工具&#xff0c;與GitHub Copilot類似。主要的功能有:代碼補全注釋…
閱讀更多...
貓毛過敏養貓人士的必備養貓好物-寵物空氣凈化器品牌分享

貓毛過敏養貓人士的必備養貓好物-寵物空氣凈化器品牌分享

許多貓奴在與貓相處一段時間后突然對貓毛過敏&#xff0c;這真是令人難受。一些人認為對貓咪過敏是因為它們在空氣中飄浮的毛發引起的&#xff0c;但實際上大部分人之所以過敏是因為對貓身上一種微小的蛋白質過敏。這種導致過敏的蛋白質附著在貓咪的一些皮屑上。我們都知道貓咪…
閱讀更多...
前端架構: 腳手架通用框架封裝之入口文件開發(教程一)

前端架構: 腳手架通用框架封裝之入口文件開發(教程一)

腳手架入口文件開發 創建腳手架項目: abc-cli $ mkdir abc-cli && cd abc-cli 全局安裝 lerna, $ npm i -g lerna 基于 lerna 完成項目初始化 $ lerna init 基于 lerna 創建腳手架 cli $ lerna create cli一路回車 好現在生成了一個 cli 的模板&#xff0c;目前需要…
閱讀更多...
Qt 中Json的構造和解析簡單例子

Qt 中Json的構造和解析簡單例子

概述: Qt中使用Json比較方便&#xff0c;不像純C需要導入CJson RapidJson JsonCpp等第三方的庫&#xff0c;主要使用到QJsonDocument、QJsonObject對象即可 1、如何構造一個json字符串 假如我們需要構造 {"cmd":"1001","data":{"content&q…
閱讀更多...
Linux 下安裝Jupyter

Linux 下安裝Jupyter

pip3 install jupyter pip3 install ipython -------------------------------------------- pip3 install jupyterlab jupyter lab pip3 list | grep jupyterlab 啟動&#xff1a; python3 -m jupyter lab 2.安裝朱皮特 pip3 install -i https://pypi.douban.com/simpl…
閱讀更多...
高性能的key-value數據庫Redis 介紹

高性能的key-value數據庫Redis 介紹

Redis 是一個高性能的key-value數據庫。 Redis是一個開源的鍵值存儲系統&#xff0c;通常用于緩存和消息傳遞。它支持多種類型的數據結構&#xff0c;如字符串、列表、集合、散列表和有序集合等。Redis的特點是提供了高性能、靈活性和可伸縮性。 Redis的主要特點包括&#xff…
閱讀更多...
Pytorch學習 day02（加載數據）

Pytorch學習 day02（加載數據）

加載數據 * Dataset提供一種方式&#xff1a;來獲取數據及其label&#xff0c;給數據進行編號 * Dataloader為神經網絡提供不同的數據形式 Dataset的組織形式有很多種&#xff0c;例如&#xff1a; 將label放在文件夾名上&#xff0c;如下&#xff1a; #Dateset # --train #…
閱讀更多...
Python算法題集_組合總和

Python算法題集_組合總和

Python算法題集_組合總和 題39&#xff1a;組合總和1. 示例說明2. 題目解析- 題意分解- 優化思路- 測量工具 3. 代碼展開1) 標準求解【值傳遞回溯】2) 改進版一【引用傳遞堆棧回溯】3) 改進版二【過程值列表緩存遍歷后檢索】 4. 最優算法5. 相關資源 本文為Python算法題集之一的…
閱讀更多...
.halo勒索病毒的最新威脅：如何恢復您的數據？

.halo勒索病毒的最新威脅：如何恢復您的數據？

尊敬的讀者&#xff1a; 隨著科技的發展&#xff0c;網絡安全已經成為我們日常生活中不可忽視的重要議題。其中&#xff0c;勒索病毒是當前網絡安全威脅中的一大挑戰&#xff0c;而“.halo”勒索病毒更是近期備受關注的惡意軟件之一。本文將介紹關于“.halo”勒索病毒的背景知…
閱讀更多...
AI新工具(20240227) StickerBaker文本生成貼紙的工具；Mistral Large；Rewind等

AI新工具(20240227) StickerBaker文本生成貼紙的工具；Mistral Large；Rewind等

StickerBaker - 基于Replicate和Fly.io技術&#xff0c;100%開源的制作貼紙的工具 StickerBaker是一個基于人工智能的貼紙創作工具&#xff0c;允許用戶通過輸入特定的提示語句生成獨特的貼紙。這個工具使用了Replicate平臺來生成貼紙&#xff0c;同時依托于Fly.io作為其基礎設…
閱讀更多...
算法項目外包的收費方式

算法項目外包的收費方式

針對算法研究性項目的收費方式和注意事項&#xff0c;這取決于項目的具體性質、規模和所涉及的技術領域。以下是一些常見的收費方式和需要注意的問題&#xff0c;希望對大家有所幫助。北京木奇移動技術有限公司&#xff0c;專業的軟件外包開發公司&#xff0c;歡迎交流合作。 收…
閱讀更多...
Python學習DAY09_文件和異常

Python學習DAY09_文件和異常

文件和異常 實際開發中常常會遇到對數據進行持久化操作的場景&#xff0c;而實現數據持久化最直接簡單的方式就是將數據保存到文件中。 在 Python 中實現文件的讀寫操作其實非常簡單&#xff0c;通過 Python 內置的 open 函數&#xff0c;我們可以指定文件名、操作模式、編碼信…
閱讀更多...
最新文章

Copyright @ 2022~2023