1.用dfs解決，首先這題的方格圖形就很像一個走迷宮的類型，迷宮想到dfs，最中心點視為起點，起點有兩個小人在這個方格里面對稱行動，直到走出迷宮（一個人走出來了另一個人就也走出來了，而走過的點會被標記，所以一個人不用擔心走到另一個人的路線上，因此只用研究一個人走迷宮問題即可）。如示：
2.走迷宮就要考慮坐標問題，dx,dy分別表示橫縱坐標的變化量，畫圖比較好看走上下左右的變化量是什么
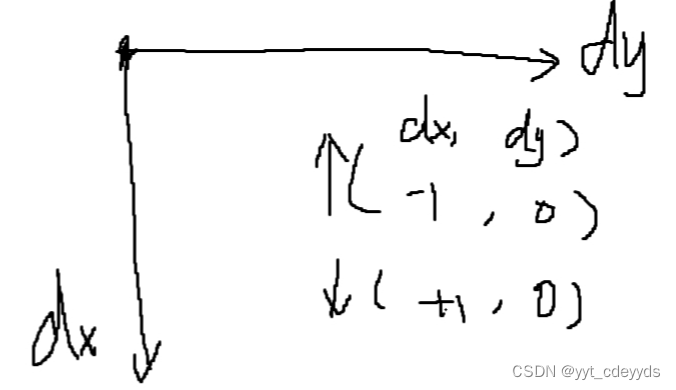
3.代碼如下
- 很貼dfs模板，dfs里面先if判斷“輸出”或者結果的答案；for循環在一個位置上可能的四個方向的選擇；for內部if判斷這個選擇行不行，行的話標記已選擇，向前走一步即dfs，再次退回到這個位置的時候再把這個選擇抹掉。
- 只不過多了坐標的變化，因為都是處于（x,y）位置上，試探性往一個方向走，不管這個方向可不可以，最終我都會退回到這個位置上，再去判斷這個位置上的另外三種可能性，所以判斷完if，肯定還是要退回來的，if只是一個試探。
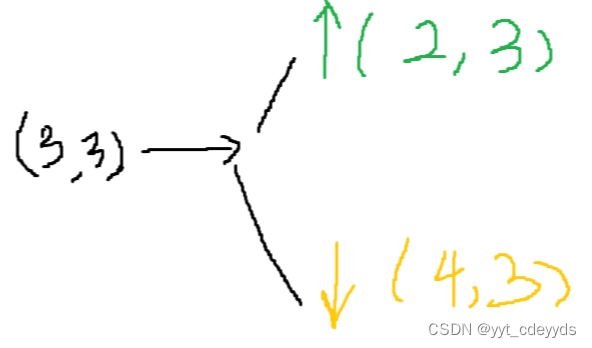
- 因為從中心（3,3）開始，所以一開始是dfs(3,3),記得把此點設置已走過再開始dfs.
- 關于對稱點的坐標變化，可以看見橫縱坐標加起來和都是6，發現這個小規律可以寫的不復雜一些。
#include<iostream>
using namespace std;int dx[] = { 0,-1,1,0,0 };
int dy[] = { 0,0,0,-1,1 };
bool vis[10][10];
int cnt = 0;
void dfs(int x, int y)
{if (x == 0 || y == 0 || x == 6 || y == 6) {cnt++;return;}for (int i = 1; i <= 4; i++) {x += dx[i];y += dy[i];if (!vis[x][y]) {vis[x][y] = 1;vis[6 - x][6 - y] = 1;dfs(x, y);vis[6 - x][6 - y] = 0;vis[x][y] = 0;}x -= dx[i];y -= dy[i];}
}
int main() {vis[3][3] = 1;dfs(3, 3);cout << cnt / 4 << endl;return 0;
}
)
