Prim算法和Kruskal算法都是解決最小生成樹問題的經典算法。最小生成樹是原圖的最小連通子圖,它包含原圖的全部結點,且保持圖連通的所有邊代價和最小。一個連通圖可能有多個最小生成樹。
一、Prim算法
含義
Prim算法,也被稱為普里姆算法,是圖論中的一種算法,主要用于在加權連通圖中搜索最小生成樹。這意味著通過Prim算法搜索到的邊子集所構成的樹中,不但包括了連通圖里的所有頂點,且其所有邊的權值之和亦為最小。
主要思想:從某個頂點開始,不斷選擇與當前生成樹相連的最小權值的邊,將其對應的頂點加入到生成樹中,直到所有頂點都加入到生成樹中為止
算法步驟
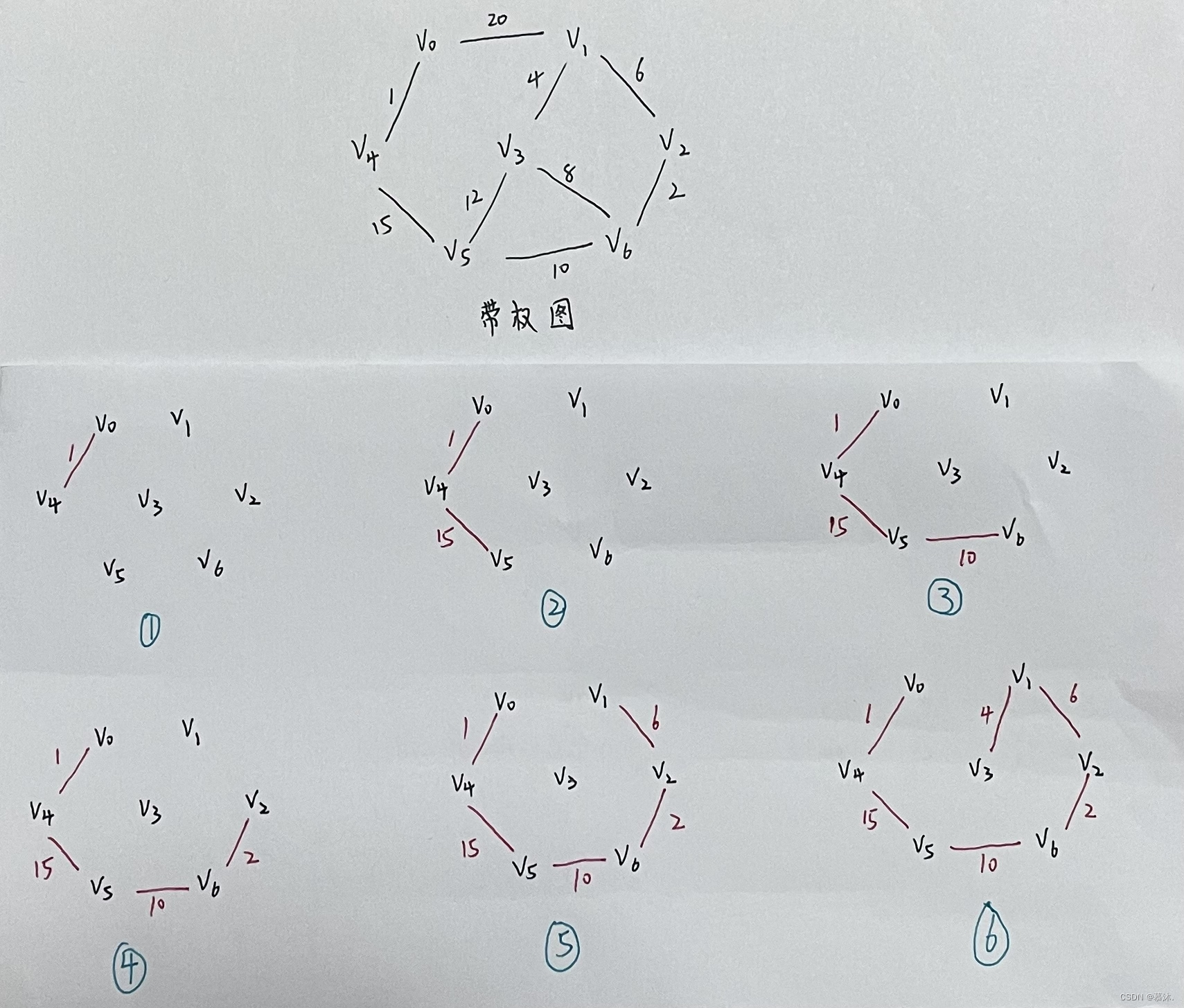
(1)初始狀態:U={u0},TE={}。其中,u0是頂點集合 V中的某一個頂點。
(2)在所有u屬于U,U屬于V-U的邊(u,v)屬于E中找一條權值最小的邊(u0,v0),將這條邊加進集合TE中,同時將此邊的另一頂點v0并入U。
這一步驟的作用是在邊集E里找一條兩個頂點分別在集合 U和V-U中且權值最小的邊,把這條邊添加到邊集 TE 中,并把這條邊上不在U中的那個頂點加入到U中。
13
(3)如果U=V,則算法結束;否則重復步驟(2)。
圖解
一、Kruskal算法
含義
Kruskal算法是一種用來查找最小生成樹的算法,它使用的貪心準則是從剩下的邊中選擇不會產生環路且具有最小權值的邊加入到生成樹的邊集中。
主要思想:先對圖中的所有邊按照權值進行從小到大的排序,然后從小到大依次選取邊,若這條邊連接的兩個頂點不在同一個連通分量中,則將其加入生成樹中,否則舍棄,直到生成樹中包含所有頂點或者所有邊都已遍歷完
算法步驟
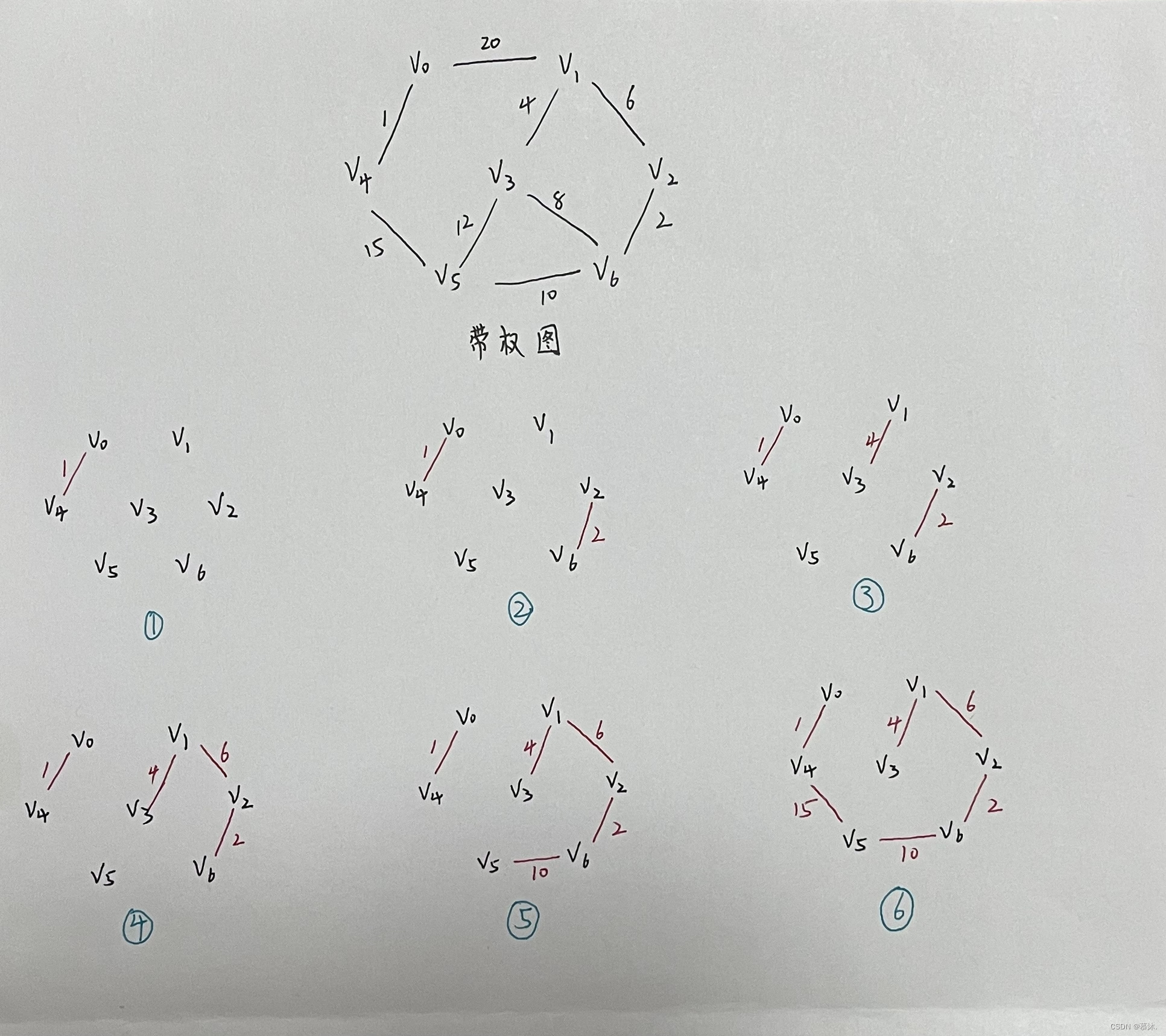
1、將圖中的所有邊按照權值從小到大進行排序。
2、初始化一個空的最小生成樹。
3、依次遍歷排序后的邊,判斷當前邊的兩個頂點是否在同一個連通分量中。如果不在同一個連通分量中,則將該邊加入最小生成樹中,并將這兩個頂點合并到同一個連通分量中。如果已經在同一個連通分量中,則跳過該邊,繼續遍歷下一條邊。
4、重復步驟3,直到最小生成樹中包含了所有的頂點,或者所有的邊都已經遍歷完畢。
圖解
三、Prim算法和Kruskal算法的區別
1、時間復雜度
Prim算法的時間復雜度為O(V^2),其中V為頂點的個數;
而Kruskal算法的時間復雜度為O(ElogE),其中E為邊的個數。在E遠大于V的情況下,Kruskal算法更加高效。
2、實現方式
Prim算法可以使用鄰接矩陣或鄰接表來表示圖,并且需要使用堆來維護當前生成樹與剩余頂點之間的邊的權重。
Kruskal算法可以使用并查集來判斷加入的邊是否形成回路。
3、適用場景
Prim算法適用于稠密圖,即邊的數量接近于頂點數量的平方;
而Kruskal算法適用于稀疏圖,即邊的數量接近于頂點數量的線性。





:Docker與虛擬化技術比較)






)






