"The only person you are destined to become is the person you decide to be." - Ralph Waldo Emerson

1. 題目描述

2. ?題目分析與解析
這個題目開始讀題的時候是有點不好理解題意的,因此我先做個圖讓大家對于題意有更好更直觀的理解再來分析題目。
比如對于這個測試用例:

實際上points就是氣球的寬度,可視化如下:
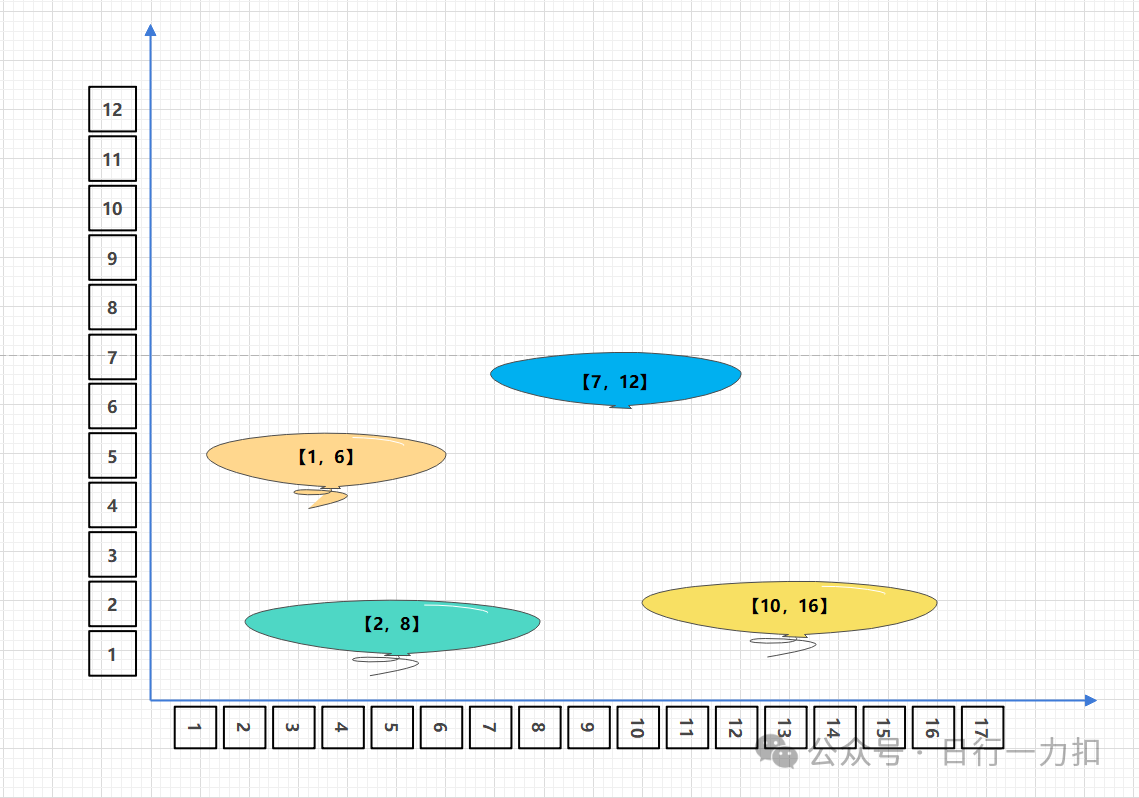
而題目要求的就是引爆所有氣球所必須射出的 最小 弓箭數 ,對于上述情況,那么就需要以下紅色的兩支箭:
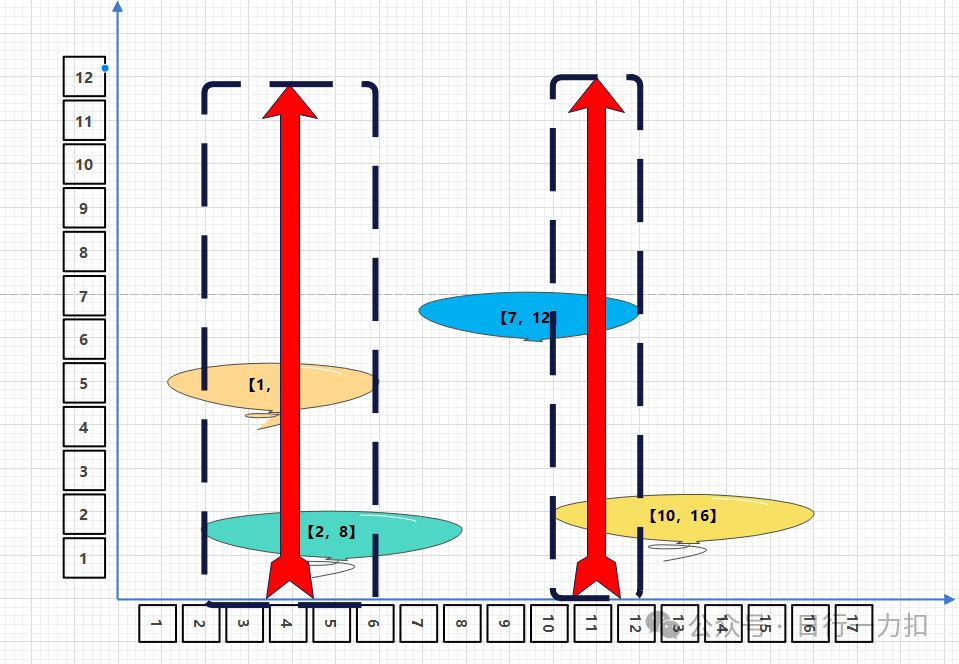
其中虛線框就是表示兩支箭的可以橫向移動的范圍。第一支箭從【2,6】都可以射出從而擊破兩個氣球,第二支箭從【10,12】都可以射出擊破剩下的兩個氣球。
2.1 思路一
可以看出本題的實質就是在找能夠涵蓋所有氣球的最小交集個數。那么我們首先應該想到的是排序,經過排序后,然后遍歷每一個區間,查看當前區間能夠附帶擊破的氣球的個數,比如如下圖:
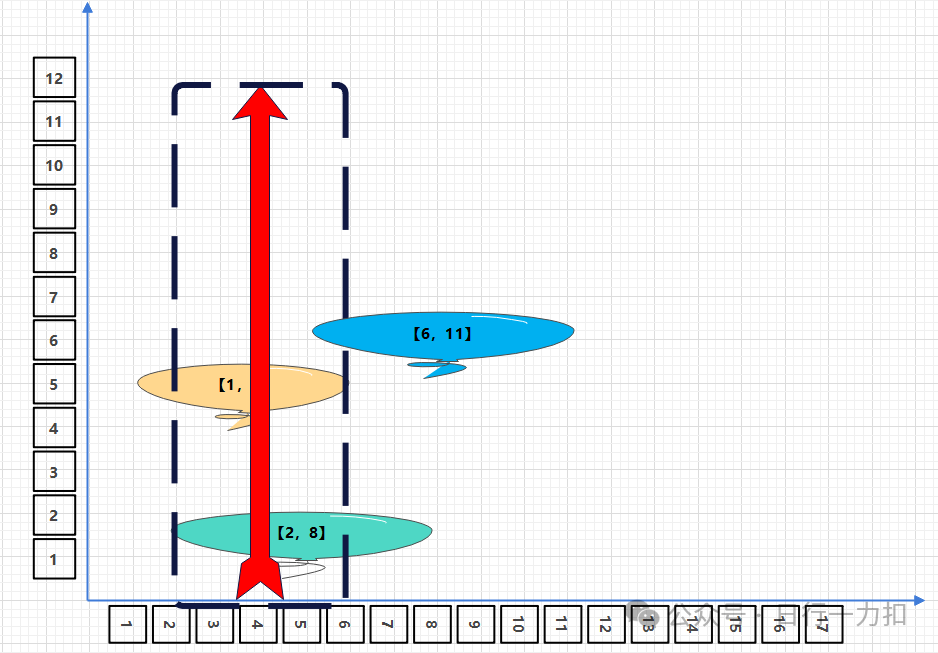
首先遍歷第一個區間【1,6】,查看每一個位置能夠附帶擊破的氣球的個數,在數字1的位置,發現只能附帶擊破自己本身1個氣球,在【2,4】發現能擊破兩個,但是在【5,6】(因為等于5就可以擊破藍色氣球:滿足 ?xstart ≤ x ≤ x``end,則該氣球會被 引爆 ),所以我們肯定得將箭設置成能擊破最多個數氣球的位置,也就是擊破三個氣球,然后移除這些已經被擊破的氣球,繼續尋找下一個區間,以此循環,直到沒有剩余的氣球。
代碼思路:
-
初始化兩個變量,一個用來統計刪除區間的位置,一個用來統計結果
-
按照區間的開始位置進行從小到大排序
-
從最小的區間開始,查看每一個數字射出箭能夠擊破的最大氣球數以及擊破氣球的位置
-
也就是判斷某個數字能否被某些區間所包含,即是否大于等于區間的最小值且小于等于區間的最大值
-
找到最多的能被包含的位置及相關區間,刪除這些區間
-
-
從當前集合中取出下一個最小區間重復以上步驟直到集合為空
-
返回結果
但是理所當然的報了超時,因為我們嘗試去遍歷了每一個可能射出箭的位置:
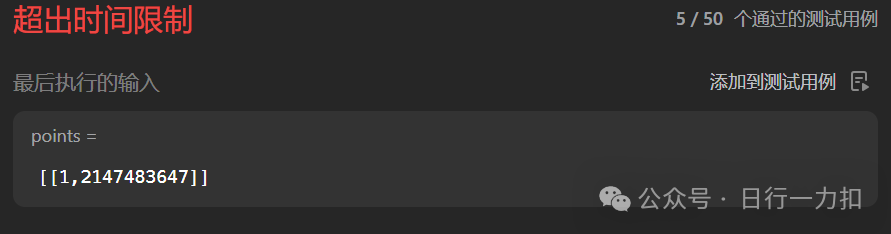
2.2 思路二
根據上面的思路,其實我們的本質就是找每個區間和其余區間的最大交集個數。
而因為如果我們按照區間的開始位置從小到大進行排序,那么我們就需要根據下一個區間的開始位置是否小于等于當前遍歷區間的結束位置,如下,假設現在遍歷第一個藍色區間:
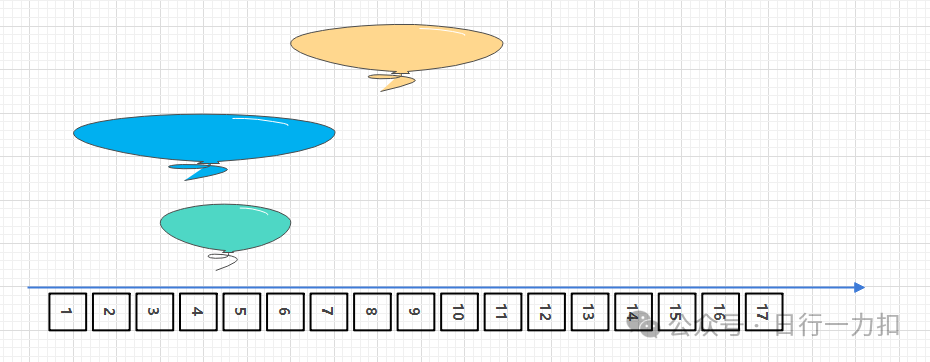
我們發現綠色的開始位置小于藍色氣球的結束位置,所以我們就可以斷定他們倆有交集(因為左端點已經經過排序了的)。然后再看下一個區間也就是黃色氣球,發現還是有交集,那么我們是不是就可以斷定這一支箭一定就可以一串三呢?
答案是否定的,雖然對于上述圖中是可以從x=6射出一只箭來打破這三個氣球,然后從剩余氣球的第一個位置繼續遍歷,但是如果是如下的情況呢?
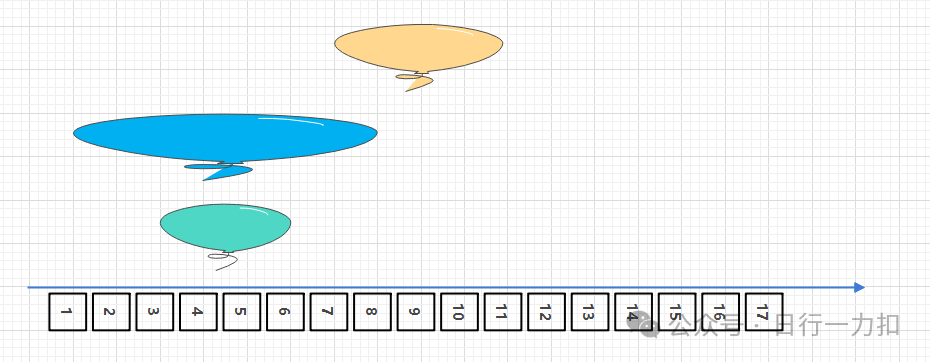
這時可以發現,雖然遍歷的第一個藍色氣球和黃色綠色兩個氣球都相交,但是我們并不能用一只箭將他們全部射破,因為綠色和黃色并不像上面開始的圖中給出的示例一樣能夠在 x=6處相交。
所以此時要注意,在判斷完畢第一個藍色氣球和綠色氣球之后,我們需要把結束位置更新,更新為 6,因為綠色氣球必須要一只 x<=6 的箭來射穿它。
這時如果結束位置是6,我們再來判斷黃色氣球的開始位置和當前區間也就是 【1,6】是否相交,發現是不可以的,就可以斷定需要一只箭來射穿前兩個氣球。然后我們再從黃色氣球開始向后按照之前的步驟繼續發出箭。
所以核心點就是: 我們一定要把結束位置更新為走過的氣球中的最小值
所以根據以上性質,我們可以給出以下代碼思路:
代碼思路:
-
對氣球區間進行升序排序
-
遍歷每一個區間,查看當前區間的下一個區間的開始位置是否小于等于當前區間的結束位置
-
如果滿足,就將遍歷的區間索引++,也就相當于移除了這個區間,然后更新右端點為兩者的最小值。
-
-
如果走到某一個區間發現不滿足上述條件,那么直接射出一只箭,然后遍歷剩下的區間
小錯誤排查:
但是按照以上思路求解發現了一個問題,就是對于該測試用例:
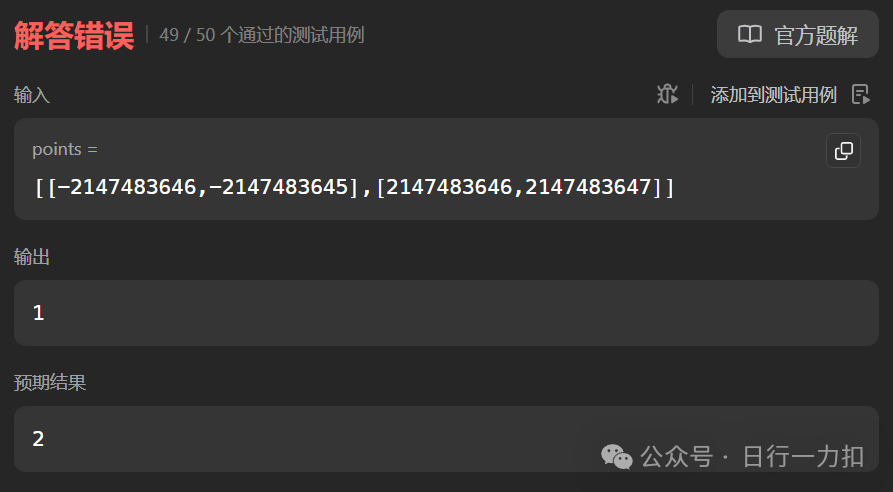
發現解答錯誤,然后我debug了一下,發現按照從小到大排序是這樣的:

通過排查了一番,找到了原因如下:
在排序時,我是用如下代碼:
? ? ? ?//1. 對氣球區間進行升序排序Arrays.sort(points, (o1, o2) -> o1[0] - o2[0]);
該代碼片段是使用一個自定義比較器對二維數組points進行排序的Java代碼。這個比較器是一個lambda表達式,它比較兩個區間的開始點o1[0]和o2[0]。
這個比較器通過計算兩個開始點的差值o1[0] - o2[0]來決定排序順序。在Java中,Comparator接口期望的返回值為負數、零或正數,分別表示第一個參數小于、等于或大于第二個參數。
但是因為測試用例中整數值接近Integer類型的極限,所以這個比較器的計算可能會導致整數溢出:
-
如果
o1[0]是一個非常大的正數,而o2[0]是一個負數,那么理論上o1[0]應該大于o2[0]。 -
但是如果
o1[0]和o2[0]的差值大于Integer.MAX_VALUE(即2147483647),那么計算結果將會溢出,導致返回一個負值。 -
這會使得排序函數錯誤地認為
o1[0]小于o2[0]。
為了避免整數溢出,那么應該使用Integer.compare()方法來比較兩個整數,它能正確處理溢出的情況。下面是修改后的代碼:
Arrays.sort(points, (o1, o2) -> Integer.compare(o1[0], o2[0]));
使用Integer.compare()方法可以確保即使是接近整數極限的值,比較操作也會正確執行,返回正確的排序順序。
經過修改后完美解決!
2.3 思路三
在思路二中,實際上是對思路一的優化,減少了一些不必要的判斷,思路二需要不斷更新右邊界來確保正確的射出箭。那么我們可不可以不更新右邊界呢?
因為我們之所以不斷更新右邊界,就是想知道在哪個位置之前必須得射出一只箭,這是必須依賴于右邊界的值的。那我們是不是可以根據右邊界從小到大進行排序,以每一個當前區間的右邊界作為指標,判斷其余區間是否能和它相交?
這樣其實每一個右邊界就是一次極限,必須射出一只箭的極限,因為如果到了右邊界還不射出,那么當前這個氣球就無法被擊破了。所以根據以上思路,我們可以對右邊界從小到大排序,得出以下:
代碼思路:
假設給定的區間集合中的每個區間表示為一個點對[xstart, xend]
-
按照xend排序:首先將所有區間按照
xend的值從小到大排序,這樣可以確保我們每次選擇的區間都是最先結束的。 -
選擇區間:從排序后的區間列表中選擇第一個區間,這個區間的
xend將覆蓋第一個坐標點。這將是我們選擇的第一個區間。 -
覆蓋剩余的點:然后遍歷剩下的點,對于每個點,如果它沒有被當前已經選擇的區間集合中的任何一個區間覆蓋,那么我們就選擇下一個區間。我們選擇的區間是排序后列表中第一個
xstart小于或等于該點坐標的區間。 -
重復:重復上述過程,直到所有的點都被覆蓋。
-
計數:在上述過程中,我們每選擇一個區間就將計數器加一,最后的計數器的值就是最少需要的區間數。
3. 代碼實現
3.1 思路一
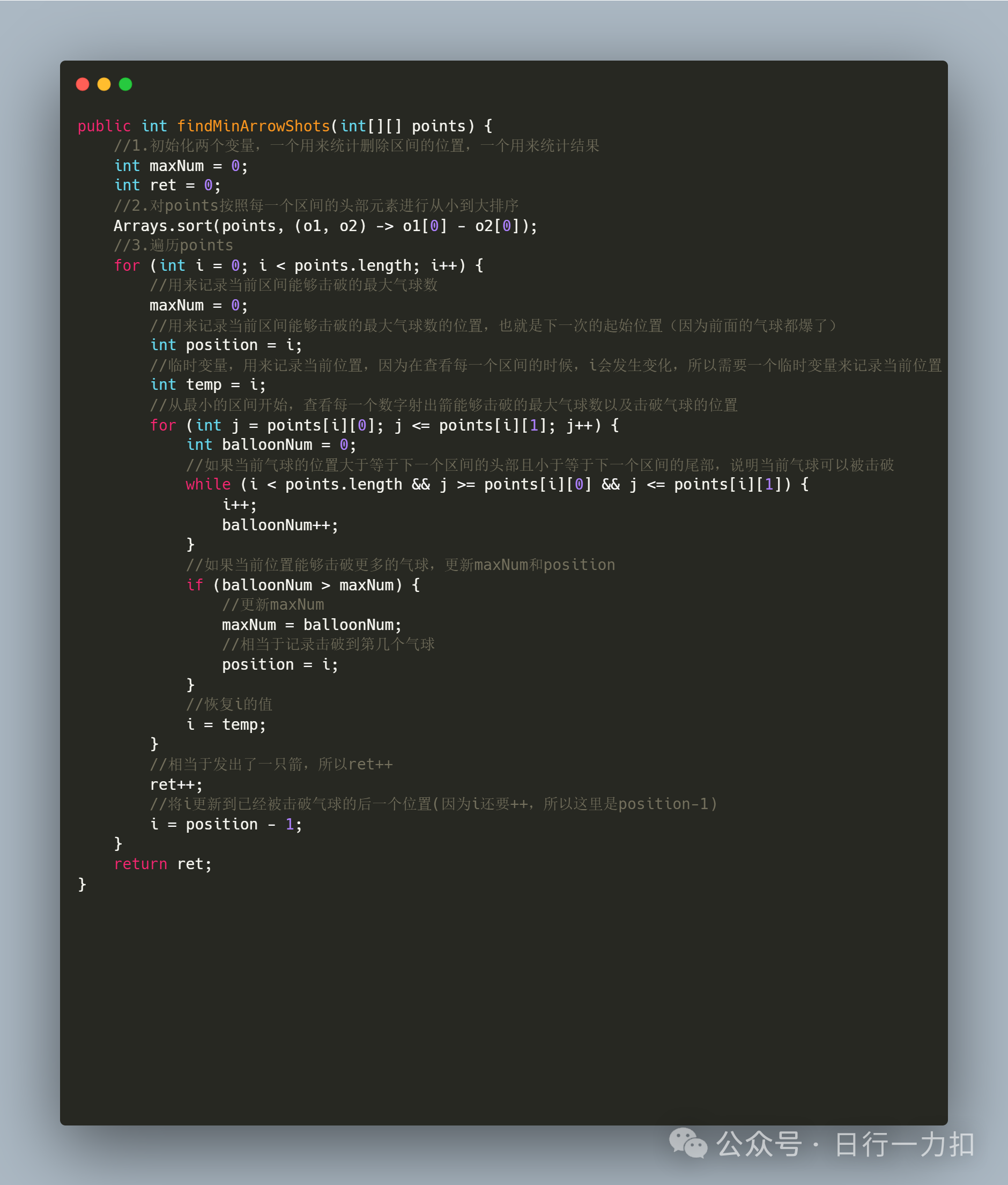

3.2 思路二
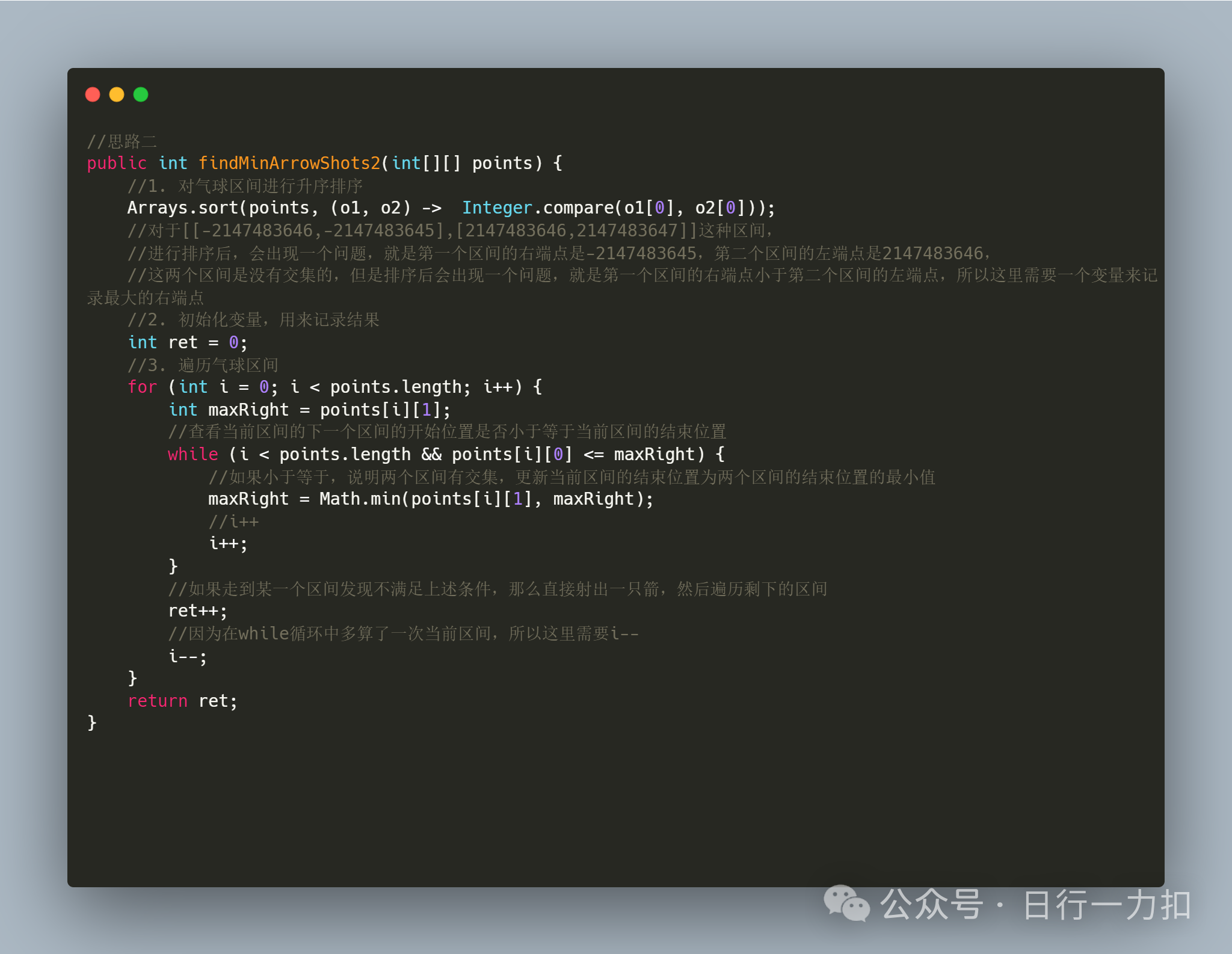
3.3 思路三
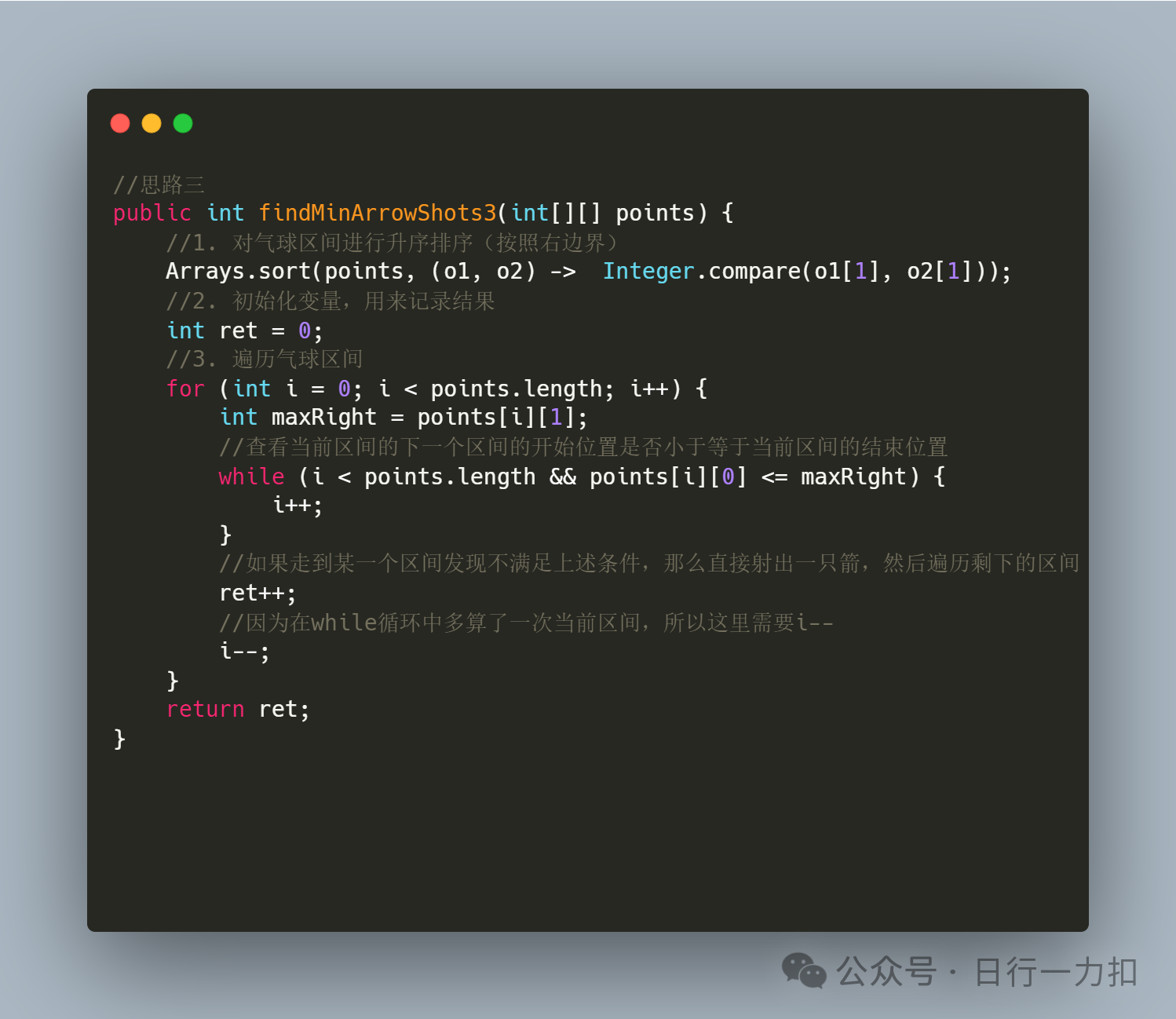
4. 相關復雜度分析
解法一:
-
時間復雜度:O(n^2),最壞情況下,每個區間都會與每個箭進行比較。
-
空間復雜度:O(1),沒有使用額外的空間,除了幾個變量以外。
解法二:
-
時間復雜度:O(n log n),排序的時間復雜度是O(n log n),遍歷區間的時間復雜度是O(n),因此總的時間復雜度是O(n log n)。
-
空間復雜度:O(1),排序可能需要O(log n)的空間復雜度(如果使用的是快速排序),但通常我們認為這是排序操作的內在空間使用,并且不會超過O(log n)。
解法三:
-
時間復雜度:O(n log n),與解法二類似,主要的時間消耗在于排序。
-
空間復雜度:O(1),同樣的理由,主要空間消耗在排序的棧空間上,不會超過O(log n)。
需要注意的是,實際的時間復雜度還取決于使用的排序算法。
在Java中,Arrays.sort()方法對于基本類型使用的是快速排序的變種,對于對象類型使用的是穩定的歸并排序,歸并排序的空間復雜度是O(n)。由于本題中排序的是int[][]類型,即對象類型,所以如果嚴格來說,空間復雜度應為O(n)。但在面試或者實際工作中,如果不是特別強調,我們通常認為這是內置的排序函數的空間復雜度,而不將其計入算法的空間復雜度中。





- 對ChatGPT的常見誤解)












)
