我之前做過自己的RTL-SDR。一直有一個疑惑。為啥rtl2832u芯片有一對差分I路，還有一對差分Q路。差分很好理解是為了抗干擾，但為啥要I和Q呢？并且我也知道不少人在自己修改的時候，保留I路對接在r820t2（跟原版一樣），而把Q路作為直采。

那么我就有一個疑惑，既然Q路可以挪作它用，并且不影響RTL-SDR本來的功能。為什么rtl2832u不只保留I路呢？而且我在電腦上寫解調軟件的時候，即使用的是原版rtlsdr，只有I路有效，但還是有交織的IQ數據輸出出來的。如果原版rtl2832u的Q路什么都沒接那么這個Q路是哪里來的呢？

雖然后來有一位朋友跟我說過，rtl2832u有兩種使用模式。第一種是類似原版的（或者說是用r820t2前端的版本），只用I路獲取中頻信號，也就是下圖(b)。第二種方式是用I路和Q路去獲取基帶信號，也就是下圖(a)。

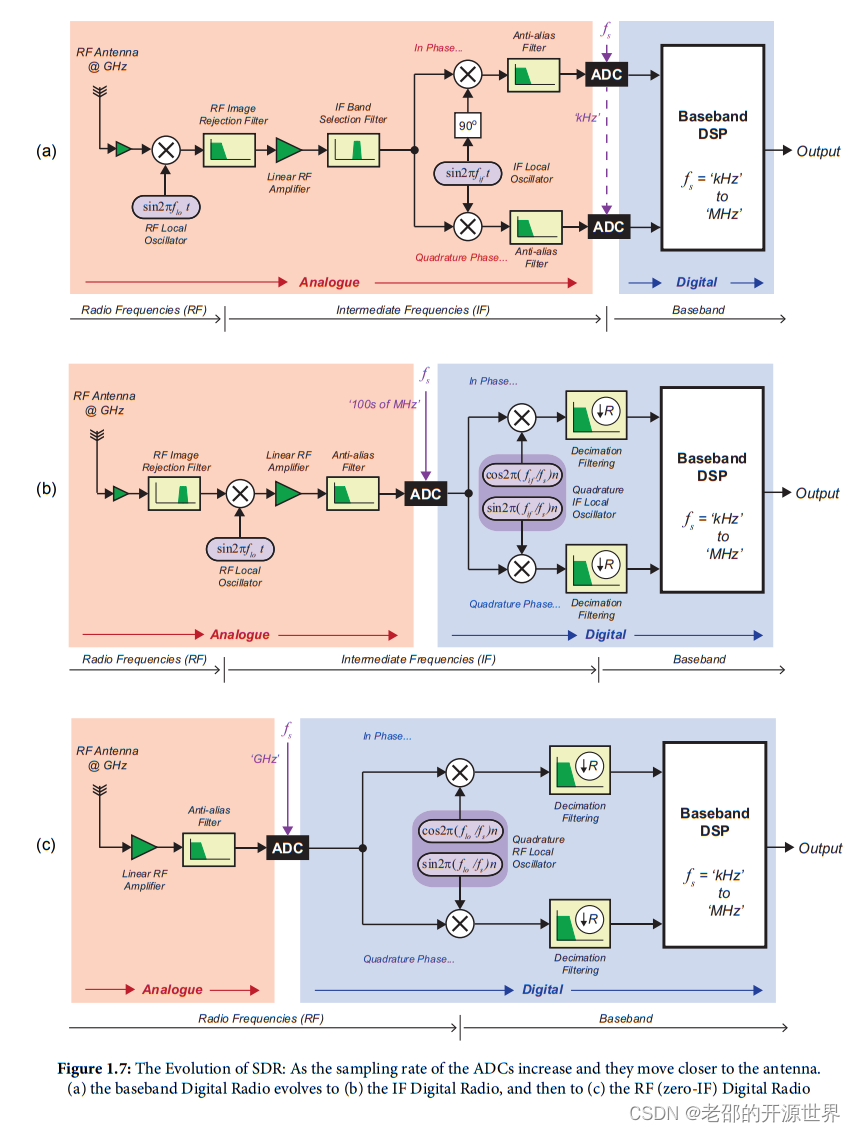
但是我當時還是沒有完全搞懂。為啥rtl2832u在采樣時中頻可以只采一路，而基帶采樣必須要分別采I路和Q路？在我看來中頻和基帶都是在頻譜上的一段區域，沒有什么區別。為啥基帶不能像中頻那樣只用一個ADC采樣，然后再到數字部分分成I和Q呢？或者說干脆不要I和Q直接用基帶信號解調了。

我也看過一些地方說IQ調制可以增加信道容量，提高頻譜利用率之類的說法，但我并沒有很深刻的理解。

直到我最近找到了一本好書:

<Fundamentals of RF and Microwave Techniques and Technologies>

這本書的第12章解答了我的一直以來的疑惑。

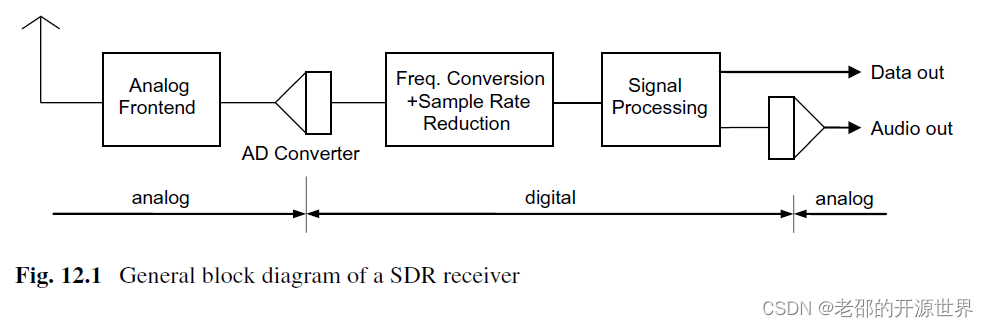
上圖是軟件無線電架構的一般化表示。我們關心的主要就是ADC前面的模擬前端。

0.如果目標頻率比較低，可以直采，那么左側模擬前端里只有一些放大器、濾波器就行，沒有混頻器。與前面彩圖(c)對應。

如果目標頻率高，左側模擬前端必須有混頻器，它又分為兩種：

1.用一個簡單的混頻器（1個余弦），下變頻到ADC支持的頻率范圍內。與彩圖(b)對應。

2.用正交混頻，也就是先分為兩路，一路用余弦，另一路用正弦，分別采樣，其中一路移相后再疊加。與彩圖(a)對應。

這時候你可能就會想，用簡單混頻器就行，為什么還要正交混頻這種復雜的結構？

關鍵在于，我們想降低ADC的采樣率，減輕后處理的負擔。

這部分說到了，為了降低采樣率，基帶信號頻率不能太高，它的頻率離0Hz比較近。這就意味著本振信號與要接收的信號頻率也比較接近，這樣混頻后才會在0Hz附近。

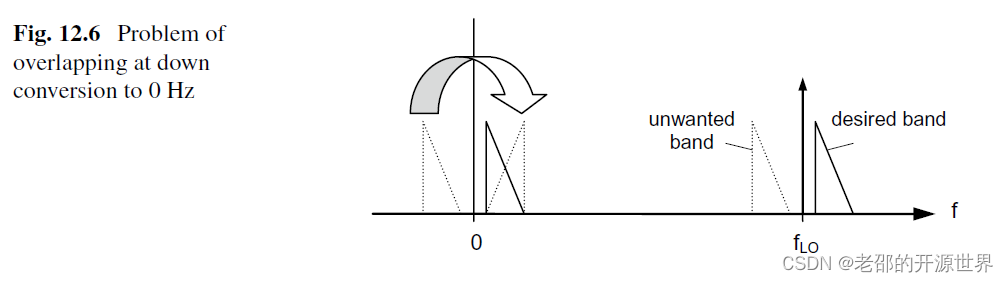
觀察上圖fLO的豎線就是本振，實線三角形是我們感興趣的信號。注意它們之間的距離比較近，好處是變頻到基帶后實線三角形離0Hz比較近。壞處你馬上就知道了。

我們可以看一下虛線三角形。這個位置實際上不一定有信號，一旦空氣中存在一個這個頻率的信號，它也會一起混頻，下搬移到負頻率處。而所有的負頻率又可以翻折到正頻率上來。一旦翻折過來，它就會和我們要的基帶信號（0Hz附近的實線三角形）重疊在一起。那就無法正常解調了。

你可能會說為什么不在剛開始接收信號的時候就用濾波器把需要的頻段與不需要的頻段分隔開呢？但所有濾波器都不是理想的，如果虛線三角形離實線三角形很遠，當然可以用濾波器區分，但如果很近就無法區分了。

所以，上面這些就解釋了，如果你要用簡單混頻器，那么就不能直接變到0Hz附近的基帶，而是搬得稍微高一點，比如對于rtlsdr來說就是3~5MHz就沒問題。而這個頻段就是我們說的中頻了。這就解釋了彩圖(b)只能在中頻起作用，不能把這個架構用于基帶采樣。

其實rtlsdr的采樣率比我們想象中的高，雖然程序中一般只用到2MSps，但這是降采樣后的，實際它的硬件采樣率可以到20多MSps。這樣它就可以采下這個中頻信號。

但如果要設計的SDR要支持更高帶寬的信號，它的中頻就必須更高，我們的ADC采樣率不夠采這么高的中頻，我們就必須考慮其它方案。也就是彩圖(a)的架構。

彩圖(a)的架構可以讓信號直接變到0Hz附近的基帶，而又不被鏡像干擾。這也是我找的這本書中重點解釋的架構。它在模擬部分就用兩個稍有不同的混頻器，分別下變頻，再把一路移相再相加，就能得到沒有鏡像干擾的基帶信號。

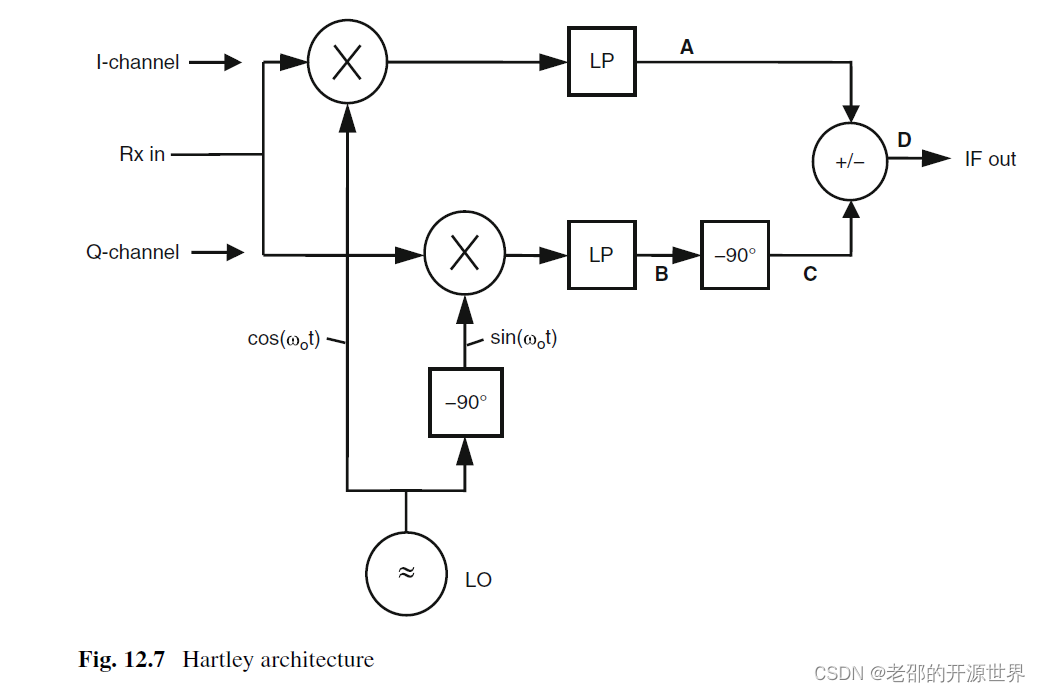
上圖就是剛剛說的架構，這種混頻器架構是1928年提出的，當時沒有SDR。所以都是模擬電路。在SDR中，其實右邊部分已經是ADC以后的軟件實現的了。

這里是對應的公式推導。公式推導證明了，在輸出端可以得到下變頻后的S(t)，它的載波從w2變為了wIF，并且輸出端的信號可以只有我們要的S(t)，而與R(t)無關。當然如果你要的是R(t)也行，只是最后一步要用減法而不是加法。

-----------------------------------------------------------------------------------------------------------------------

此書不但講了為什么要用IQ采樣基帶信號，還解釋了為啥要做IQ的幅度校正和相位校正。如果不做那么剛剛正好能約掉的項目就約不掉了。之前看到Lime官方也講過這個問題，但當時只是看到調節LimeSuite后星座圖/頻譜圖確實有一些改善。但沒理解為什么。

下面是這本書的解釋。

書中還提出了IRR這個指標，但光看公式就能看出增益和相位不平衡會帶來一些無法抵消的項目了。

_________________________________________________________________________

上文已經解釋了為啥要彩圖(a)要用IQ。但為啥彩圖(b)和(c)在數字部分還要用IQ？不清楚。。。

文中提到的書可以在Springer出版社官網免費下載。