電子技術——PN結電流關系方程
平衡狀態下的PN結
平衡狀態下的PN結界面總共有兩種電流,一種為 擴散電流 另一種為 漂移電流 。兩種電流形成的平衡區域稱為 耗散區 。
在平衡狀態擴散電流等于漂移電流,此時靜電流為0,PN結外部沒有電流:
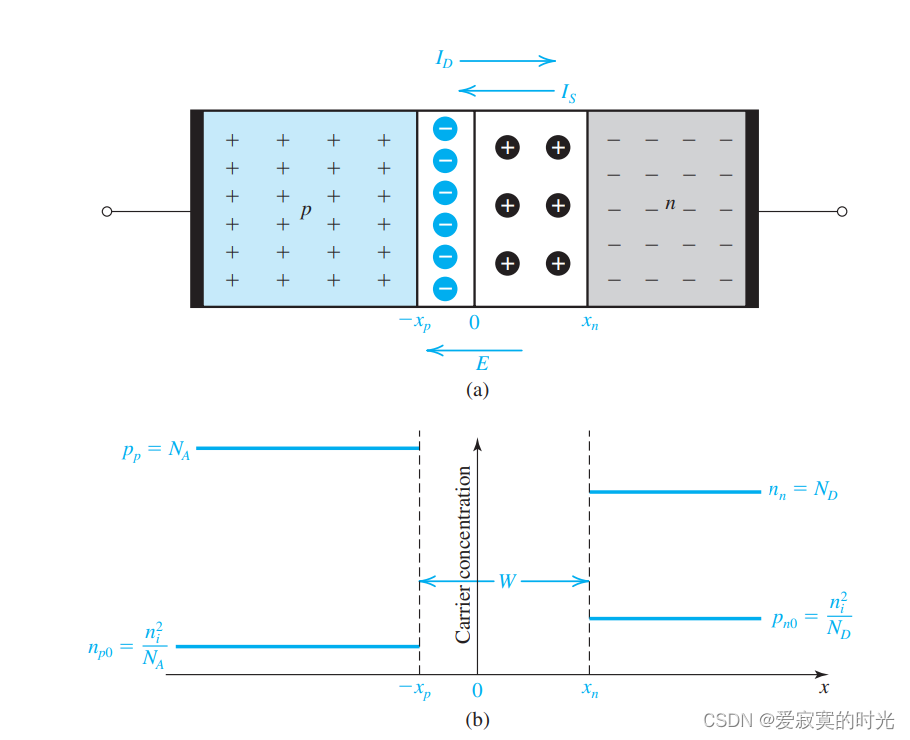
圖中 I D I_D ID? 為擴散電流, I S I_S IS? 為漂移電流。 x n x_n xn? 為耗散區 n n n 區域長度, ? x p -x_p ?xp? 為耗散區 p p p 區域長度, W W W 為耗散區寬度。
n n n_n nn? 為 n n n 區域主要載流子(電子)密度,等于摻雜濃度 N D N_D ND? , p p p_p pp? 為 p p p 區域主要載流子(空穴)密度,等于摻雜濃度 N A N_A NA? 。
p n 0 p_{n0} pn0? 為 n n n 區域次要載流子(空穴)密度,滿足 玻爾茲曼條件下的密度關系方程 p n 0 = n i 2 N D p_{n0} = \frac{n^2_i}{N_D} pn0?=ND?ni2?? , n p 0 n_{p0} np0? 為 p p p 區域次要載流子(電子)密度,滿足 n p 0 = n i 2 N A n_{p0} = \frac{n^2_i}{N_A} np0?=NA?ni2?? 。 n i n_i ni? 為平衡次載流子密度(共價鍵斷裂產生,與溫度有關),平衡條件下有 p n = n n = n i p_n = n_n = n_i pn?=nn?=ni? 。
由于擴散區中理想下不存在任何載流子,只有 貢獻原子 和 接受原子 存在,PN結界面兩邊存在不同的凈電荷,因此擴散區將形成 勢壘電壓 V 0 V_0 V0?:

勢壘電壓阻止了PN結界面的濃度進一步擴散(電壓與擴散方向相反),耗散區寬度處于恒定數值 W W W ,因此PN結處于平衡狀態。
外加偏置電壓狀態下的PN結
當PN結處于外加偏置電壓 V V V 下時,將會破壞PN結的平衡狀態,此時PN結電流與外界電流一起處于 動態平衡 狀態。
外界電流等于:
I = I D ? I S I = I_D - I_S I=ID??IS?
動態平衡下的PN結中, p p p 和 n n n 區域中的載流子密度不再是隨位置變換的恒等函數,而是指數函數:

上圖描述了PN處于 正偏置 下的濃度隨位置的變化曲線,正偏置電壓提供了更多的能量讓載流子突破勢壘電壓,增大了擴散電流。
此時PN結對外界的電流表現為界面 ? x p -x_p ?xp? 與 x n x_n xn? 的密度梯度擴散電流,等價于 I = I D ? I S I = I_D - I_S I=ID??IS? ,正偏置下表現為:
擴散電流大于漂移電流 I D > I S I_D > I_S ID?>IS? ,此時會有額外的空穴進入 n n n 區域,通過外部電路流回 p p p 區域,因此界面 x n x_n xn? 處的 p n p_n pn? 濃度上升,同理 ? x p -x_p ?xp? 界面的 n p n_p np? 濃度也上升。
對于負偏置電壓下的濃度隨位置的變化曲線:
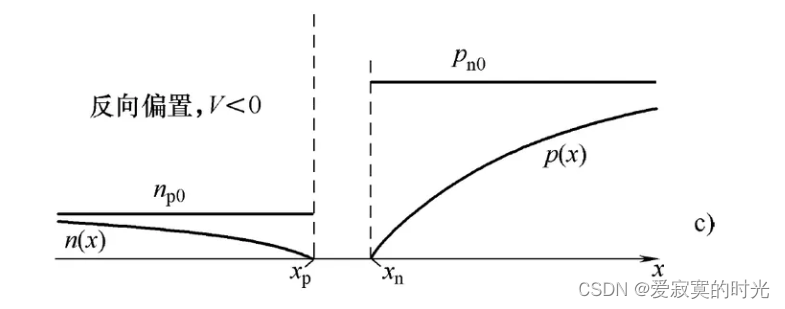
反向偏置電壓增大了擴散的壁壘能量,擴散電流幾乎為0,但漂移電流幾乎保持不變(漂移現象由粒子熱運動有關),此時 n n n 區域中的耗散區缺少空穴,空穴通過 n n n 區域進入耗散區,導致界面 x n x_n xn? 處的 p n p_n pn? 濃度下降,同理 ? x p -x_p ?xp? 界面的 n p n_p np? 濃度也下降,下降最低點為0(濃度不能為負數)。
通過半導體物理學,界面 x n x_n xn? 的密度隨外界偏置電壓的變化關系為:
p n ( x n ) = p n 0 e V / V T p_n(x_n) = p_{n0}e^{V/V_T} pn?(xn?)=pn0?eV/VT?
當 V V V 為負無窮的時候(反向偏置電壓無限大),此時 p n ( x n ) = 0 p_n(x_n) = 0 pn?(xn?)=0 ,但當 V V V 表現為正電壓的時候, p n ( x n ) p_n(x_n) pn?(xn?) 隨 V V V 指數上升(PN結單向導電性)。
同樣當 x > x n x > x_n x>xn? 密度隨位置呈現指數變化,關系為:
p n ( x ) = p n 0 + p n 0 ( e V / V T ? 1 ) e ? ( x ? x n ) / L p p_n(x) = p_{n0} + p_{n0}(e^{V/V_T} - 1) e^{-(x-x_n)/L_p} pn?(x)=pn0?+pn0?(eV/VT??1)e?(x?xn?)/Lp?
當 x = x n x = x_n x=xn? 的時候, p n ( x n ) = p n 0 e V / V T p_n(x_n) = p_{n0}e^{V/V_T} pn?(xn?)=pn0?eV/VT? 。
L p L_p Lp? 稱為 擴散長度 。
界面的梯度電流為:
J p ( x ) = ? q D p d p n ( x ) d x J_p(x) = -q D_p \frac{dp_n(x)}{dx} Jp?(x)=?qDp?dxdpn?(x)?
帶入得到:
J p ( x n ) = q ( D p L p ) p n 0 ( e V / V T ? 1 ) J_p(x_n) = q (\frac{D_p}{L_p}) p_{n0} (e^{V/V_T} - 1) Jp?(xn?)=q(Lp?Dp??)pn0?(eV/VT??1)
其中 D p D_p Dp? 為空穴的擴散速率,與空穴的漂移速率滿足 愛因斯坦關系 :
D n μ n = D p μ p = V T \frac{D_n}{\mu_n} = \frac{D_p}{\mu_p} = V_T μn?Dn??=μp?Dp??=VT?
V T V_T VT? 為熱電壓 μ p \mu_p μp? 為空穴的漂移速率。
同理:
J n ( ? x p ) = q ( D n L n ) n p 0 ( e V / V T ? 1 ) J_n(-x_p) = q (\frac{D_n}{L_n}) n_{p0} (e^{V/V_T} - 1) Jn?(?xp?)=q(Ln?Dn??)np0?(eV/VT??1)
總電流為:
I = A ( J p + J n ) = A q ( D p L p p n 0 + D n L n n p 0 ) ( e V / V T ? 1 ) = A q n i 2 ( D p L p N D + D n L n N A ) ( e V / V T ? 1 ) I = A(J_p + J_n) = Aq(\frac{D_p}{L_p} p_{n0} + \frac{D_n}{L_n} n_{p0}) (e^{V/V_T} - 1) = Aqn^2_i (\frac{D_p}{L_p N_D} + \frac{D_n}{L_n N_A}) (e^{V/V_T} - 1) I=A(Jp?+Jn?)=Aq(Lp?Dp??pn0?+Ln?Dn??np0?)(eV/VT??1)=Aqni2?(Lp?ND?Dp??+Ln?NA?Dn??)(eV/VT??1)
當 V V V 為負無窮的時候,我們知道 I I I 的大小等于 I S I_S IS? ,因此:
I = I S ( e V / V T ? 1 ) I = I_S (e^{V/V_T} - 1) I=IS?(eV/VT??1)
I S = A q n i 2 ( D p L p N D + D n L n N A ) I_S = Aqn^2_i (\frac{D_p}{L_p N_D} + \frac{D_n}{L_n N_A}) IS?=Aqni2?(Lp?ND?Dp??+Ln?NA?Dn??)
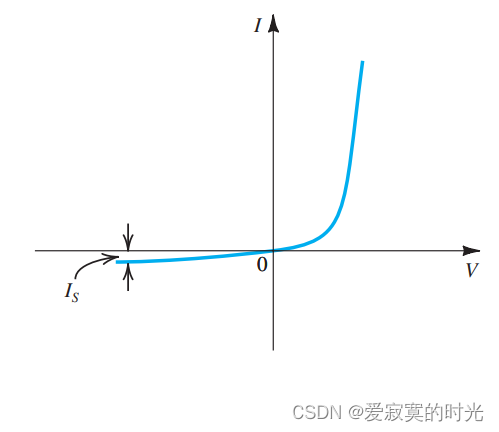
I S I_S IS? 稱為 飽和電流 ,因為與界面面積 A A A 有關,又稱為 比例電流 。 I S I_S IS? 又正比于 n i 2 n^2_i ni2? ,因此又和溫度有關。表達式 I = I S ( e V / V T ? 1 ) I = I_S (e^{V/V_T} - 1) I=IS?(eV/VT??1) 的圖像為:


掛載硬盤/數據盤詳細操作和開機自動掛載的兩種方式)


之同態濾波)



)




)




