P8680 [藍橋杯 2019 省 B] 特別數的和

題目描述

小明對數位中含有?2、0、1、9?的數字很感興趣（不包括前導?00），在?1?到 40?中這樣的數包括?1、2、9、10?至 32、39?和 40，共28?個，他們的和是574。

請問，在?1?到?n?中，所有這樣的數的和是多少？

輸入格式

輸入一行包含一個整數?�n。

輸出格式

輸出一行，包含一個整數，表示滿足條件的數的和。

將輸入的數按照不同的位數進行分類，然后將他們的每一項數位提取出來進行判斷

如果符合條件則累加

#include<bits/stdc++.h>
using namespace std;
int a[6];
int main()
{int sum=0;int n;cin>>n;for(int i=1;i<=n;i++){a[1]=i%10;//個位a[2]=i/10%10;//十位a[3]=i/100%10;//百位a[4]=i/1000%10;//千位a[5]=i/10000%10;//萬位if(i<10){if(i==2||i==1||i==9){sum+=i;}}if(i>=10&&i<100){for(int j=1;j<3;j++){if(a[j]==2||a[j]==1||a[j]==9||a[j]==0){sum+=i;break;}}}if(i>=100&&i<1000){for(int j=1;j<4;j++){if(a[j]==2||a[j]==1||a[j]==9||a[j]==0){sum+=i;break;}}}if(i>=1000&&i<10000){for(int j=1;j<5;j++){if(a[j]==2||a[j]==1||a[j]==9||a[j]==0){sum+=i;break;}}}}cout<<sum;return 0;
}

L-shapes

題目描述

An L-shape is a figure on gridded paper that looks like the first four pictures below. An L-shape contains exactly three shaded cells (denoted by *), which can be rotated in any way.

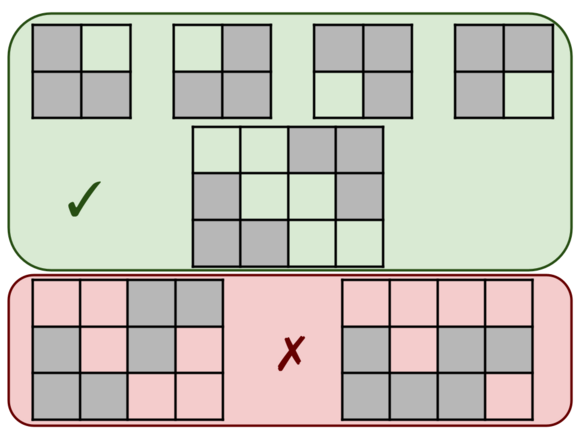
You are given a rectangular grid. Determine if it contains L-shapes only, where L-shapes can't touch an edge or corner. More formally:

• Each shaded cell in the grid is part of exactly one L-shape, and
• no two L-shapes are adjacent by edge or corner.

For example, the last two grids in the picture above do not satisfy the condition because the two L-shapes touch by corner and edge, respectively.

輸入格式

The input consists of multiple test cases. The first line contains an integer?t（1≤t≤100?) — the number of test cases. The description of the test cases follows.

The first line of each test case contains two integers?n?and?m?( 1≤n,m≤50?) — the number of rows and columns in the grid, respectively.

Then?n?lines follow, each containing?m?characters. Each of these characters is either '.' or '*' — an empty cell or a shaded cell, respectively.

輸出格式

For each test case, output "YES" if the grid is made up of L-shape that don't share edges or corners, and "NO" otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

題意翻譯

L形在網格紙上形如下面的前四張圖片。L形正好包含三個陰影單元（用*表示），可以以任何方式旋轉。

現給你一個矩形網格。確定它是否僅包含L形，其中L形不能接觸邊或角，也就是說網格中的每個陰影單元正好是一個L形的一部分，并且沒有兩個L形通過邊或角相鄰。

例如，上圖中的最后兩個網格不滿足條件，因為兩個L形分別通過角和邊緣接觸。

如果網格滿足條件，則輸出“YES”，否則輸出“NO”。

遍歷，當掃到*的時候，將其標記為1，遍歷到1時對周圍進行掃描，符合條件則將L型都變為0

最后再掃描時如果還掃到1則輸出NO,否則輸出YES

#include<bits/stdc++.h>
using namespace std;
int a[55][55],n,m,t;
char s;
void find(int i,int j)
{if(a[i+1][j]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&!a[i][j-1]&&!a[i][j+1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){a[i][j]=a[i+1][j]=a[i+1][j+1]=0;return ;}if(a[i+1][j-1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&!a[i][j-2]&&!a[i][j-1]&&!a[i][j+1]&&!a[i+1][j-2]&&!a[i+1][j+1]&&!a[i+2][j-2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){a[i][j]=a[i+1][j-1]=a[i+1][j]=0;return ;}if(a[i][j+1]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&!a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j]&&!a[i+1][j+2]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){a[i][j]=a[i][j+1]=a[i+1][j+1]=0;return ;}if(a[i][j+1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&!a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+1]&&!a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){a[i][j]=a[i][j+1]=a[i+1][j]=0;return ;}
}
int main()
{cin>>t;for(int k=1;k<=t;k++){memset(a,0,sizeof(a));bool possible = true;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>s;if(s=='*')a[i][j]=1;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==1)find(i,j);}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==1){possible=false;break ;}}if (!possible) break;}if (possible) {cout << "YES\n";} else {cout << "NO\n";}}return 0;
}

P1258 小車問題

題目描述

甲、乙兩人同時從 A 地出發要盡快同時趕到 B 地。出發時 A 地有一輛小車，可是這輛小車除了駕駛員外只能帶一人。已知甲、乙兩人的步行速度一樣，且小于車的速度。問：怎樣利用小車才能使兩人盡快同時到達。

輸入格式

僅一行，三個實數，分別表示 AB 兩地的距離?s，人的步行速度?a，車的速度?b。

輸出格式

兩人同時到達 B 地需要的最短時間，保留?6?位小數。

列方程x/a=(s-2x+s-x)/b

解得時間=x/a+(s-x)/b

#include<bits/stdc++.h>
using namespace std;
int main()
{double a,b,s,x;cin>>s>>a>>b;double t;x=(2*a*s)/(3*a+b);t=x/a+(s-x)/b;cout<<fixed<<setprecision(6)<<t;
}

P10050 [CCO2022] Alternating Heights

題目描述

Troy 計劃給 CCO 的學生拍一張合影，他向你尋求幫助。

有?K?個學生，編號從?1?到?K。Troy 忘記了學生的身高，但他記得沒有兩個學生的身高相同。

Troy 有一個序列?1,2,…,A1?,A2?,…,AN?，表示合影中從左到右的學生順序。一個學生可能在?A?中出現多次。你不確定這張合影會怎么拍，但你不愿意認為 Troy 犯了錯誤。

Troy 會給你?Q?個形式為 x,y?的詢問，每個詢問為「給定學生序列 Ax?,Ax+1?,…,Ay?，他們的身高能否形成一個交替序列？」更具體地說，我們用?hi??表示第 i?個學生的身高。如果存在一種身高分配h1?,h2?,…,hK?，使得 hAx??>hAx+1??<hAx+2??>hAx+3??<…hAy??，回答?YES；否則回答?NO。

注意，每個查詢都是獨立的：也就是說，詢問?i?的身高分配與詢問?j?的身高分配無關(i！=j)。

輸入格式

第一行包含三個用空格分隔的整數?N,K?和?Q。

第二行包含?N?個整數，表示?1,2,…)A1?,A2?,…,AN?(1≤Ai?≤K)。

接下來的?Q?行，每行包含兩個用空格分隔的整數?x?和?(1≤x<y≤N)，表示一組查詢。

輸出格式

輸出?Q?行。第 i?行，輸出?YES?或者?NO，表示 Troy 的第?i?個查詢的答案。

每次進行二分查找，將中間值和左端點進行拓撲排序

如果出現環則說明矛盾，輸出NO

#include<bits/stdc++.h>
using namespace std;
int n,m,t,x,y,a[10005],f[10005];
int d[3005][3005],top[3005],in[3005];
queue<int> q;
bool check(int l,int r)
{memset(in,0,sizeof(in));memset(top,0,sizeof(top));for(int i=l+1;i<=r;i+=2){if(i-1>0) d[a[i]][++top[a[i]]]=a[i-1],in[a[i-1]]++;if(i+1<=r) d[a[i]][++top[a[i]]]=a[i+1],in[a[i+1]]++;}while(!q.empty()) q.pop();for(int i=1;i<=m;i++){if(!in[i]){q.push(i);}}int sum=0;while(!q.empty()){int p=q.front();q.pop();sum++;for(int i=1;i<=top[p];i++){in[d[p][i]]--;if(!in[d[p][i]])q.push(d[p][i]);}}return sum==m;
}
int F(int k)
{int l=k,r=n,mid,p=0;while(l<=r){mid=(l+r)/2;if(check(k,mid))p=max(p,mid),l=mid+1;elser=mid-1;}return p;
}
int main()
{cin>>n>>m>>t;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)f[i]=F(i);for(int i=1;i<=t;i++){cin>>x>>y;if(y<=f[x]){cout<<"YES"<<endl;}else{cout<<"NO"<<endl;}}return 0;
}