圖——最小生成樹實現(Kruskal算法,prime算法)

預備知識：

最小生成樹概念：

Kruskal算法：

代碼實現如下：

測試：

Prime算法：

代碼實現如下：

測試：

結語：

預備知識：

連通圖：在無向圖中，若從頂點v1到頂點v2有路徑，則稱頂點v1與頂點v2是連通的。如果圖中任意一對頂點都是連通的，則稱此圖為連通圖。

生成樹：一個連通圖的生成樹是指一個連通子圖，它含有圖中全部n個頂點，但只有足以構成一棵樹的n-1條邊。一顆有n個頂點的生成樹有且僅有n-1條邊，如果生成樹中再添加一條邊，則必定成環。

并查集：

由于本文章重點不在講述并查集，故下面我簡單描述并查集的作用，各種方法，源碼如下。

并查集的作用：可以將一個數組中的元素分為多個小組的數據結構。

方法：

findRoot（x）：查找x的根。

union(int x1, int x2)：合并x1和x2。

isSameSet(int x1, int x2)：判斷兩個數字是不是在同一個集合當中。

import java.util.Arrays;public class UnionFindSet {private int[] elem;//底層是數組public UnionFindSet(int n){this.elem = new int[n];Arrays.fill(elem,-1);//整體初始化為-1：代表根}/*** 查找x的根* @param x* @return*/public int findRoot(int x){if(x < 0){throw new IndexOutOfBoundsException("數據不合法");}while(elem[x] >= 0){x = elem[x];}return x;}/*** 合并x1和x2* @param x1* @param x2*/public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){//說明x1和x2的根是相同的，不需要進行合并return;}elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;//將x2合并到x1}/*** 判斷兩個數字是不是在同一個集合當中* @param x1* @param x2* @return*/public boolean isSameSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){return true;}else{return false;}} 
}

最小生成樹概念：

連通圖中的每一棵生成樹，都是原圖的一個極大無環子圖，即：從其中刪去任何一條邊，生成樹就不在連通；反之，在其中引入任何一條新邊，都會形成一條回路。

若連通圖由n個頂點組成，則其生成樹必含n個頂點和n-1條邊。因此構造最小生成樹的準則有三條：

(1) 只能使用圖中的邊來構造最小生成樹。

(2)?只能使用恰好n-1條邊來連接圖中的n個頂點。

(3)?選用的n-1條邊不能構成回路。

構造最小生成樹的方法：Kruskal算法和Prim算法。這兩個算法都采用了逐步求解的貪心策略。

貪心算法：是指在問題求解時，總是做出當前看起來最好的選擇。也就是說貪心算法做出的不是整體最優的選擇，而是某種意義上的局部最優解。貪心算法不是對所有的問題都能得到整體最優解。

Kruskal算法：

Kruskal算法采用全局貪心的策略，其步驟如下：

任給一個有n個頂點的連通網絡N={V,E}。

（1）首先構造一個由這n個頂點組成、不含任何邊的圖G={V,NULL}，其中每個頂點自成一個連通分量。

（2）其次不斷從E中取出權值最小的一條邊(若有多條任取其一)，若該邊的兩個頂點來自不同的連通分量（若相同則不加因為會生成環），則將此邊加入到G中。

（3）如此重復，直到所有頂點在同一個連通分量上為止。

核心：每次迭代時，選出一條具有最小權值，且兩端點不在同一連通分量上的邊，加入生成樹。

?具體過程如下圖所示：按照abc..的循序，箭頭為當前要操作的位置（不一定能添加，黑色為可添加）。

代碼實現如下：

先構造關于Edge的小根堆，由于是自定義類，故要自己實現一個比較器Comparator。

1. 定義優先級隊列存儲邊構建小根堆跟進權重進行比較。

2. 把矩陣當中的邊全部入隊列。

3. 定義并查集判斷將來兩條邊是不是在一個集合（避免構成環）。

4. 由于篇幅有限matrix之類的前文實現過這里不在實現有需要的友友可以前往圖的概念

static class Edge{public int srcIndex;public int destIndex;public int weight;public Edge(int srcIndex,int destIndex,int weight){this.srcIndex = srcIndex;this.destIndex = destIndex;this.weight = weight;}}public int kruskal(GraphByMatrix minTree){//1. 定義優先級隊列 存儲邊 構建小根堆 跟進權重進行比較PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){@Overridepublic int compare(Edge o1,Edge o2){return o1.weight - o2.weight;}});int n = matrix.length;//2. 把矩陣當中的邊全部入隊列for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){//因為是無向圖，所以只入一半就可以 i < j 即可if(i < j && matrix[i][j] != Integer.MAX_VALUE){Edge edge = new Edge(i,j,matrix[i][j]);minHeap.offer(edge);}}}//3、最后整個的權重int totalWeight = 0;int size= 0;//4.定義并查集 判斷將來兩條邊 是不是在一個集合UnionFindSet ufs = new UnionFindSet(n);//5. 出優先級隊列的n-1條邊while(size < n-1 &&!minHeap.isEmpty()){Edge min  = minHeap.poll();int srcIndex = min.srcIndex;int destIndex = min.destIndex;//判斷是不在在同一個集合當中,在一個集合 就不能添加if(!ufs.isSameSet(srcIndex,destIndex)){//打印選出的邊System.out.println("選擇的邊: "+ arrayV[srcIndex] + "-> "+ arrayV[destIndex] + ":"+matrix[srcIndex][destIndex]);?minTree.addEdgeUseIndex(srcIndex,destIndex,min.weight);totalWeight += min.weight;//添加完成之后，說明 可以 合并到同一個集合ufs.union(srcIndex,destIndex);size++;}}//如果是 選出n-1條邊，否則就說明不是連通圖if(size == n-1){return totalWeight;}//不是連通圖， 可能選不出n-1條邊  假設一個圖中，有其他的頂點獨立著return -1;}private void addEdgeUseIndex(int srcIndex,int destIndex,int weight) {matrix[srcIndex][destIndex] = weight;//如果是無向圖 那么相反的位置 也同樣需要置為空if(!isDirect) {matrix[destIndex][srcIndex] = weight;}}

測試：

測試代碼對應的圖：

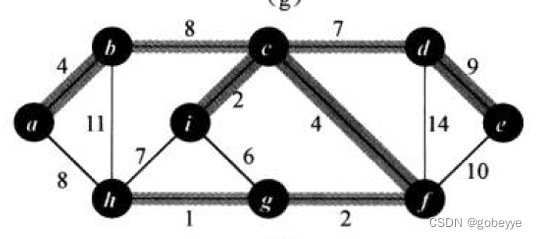
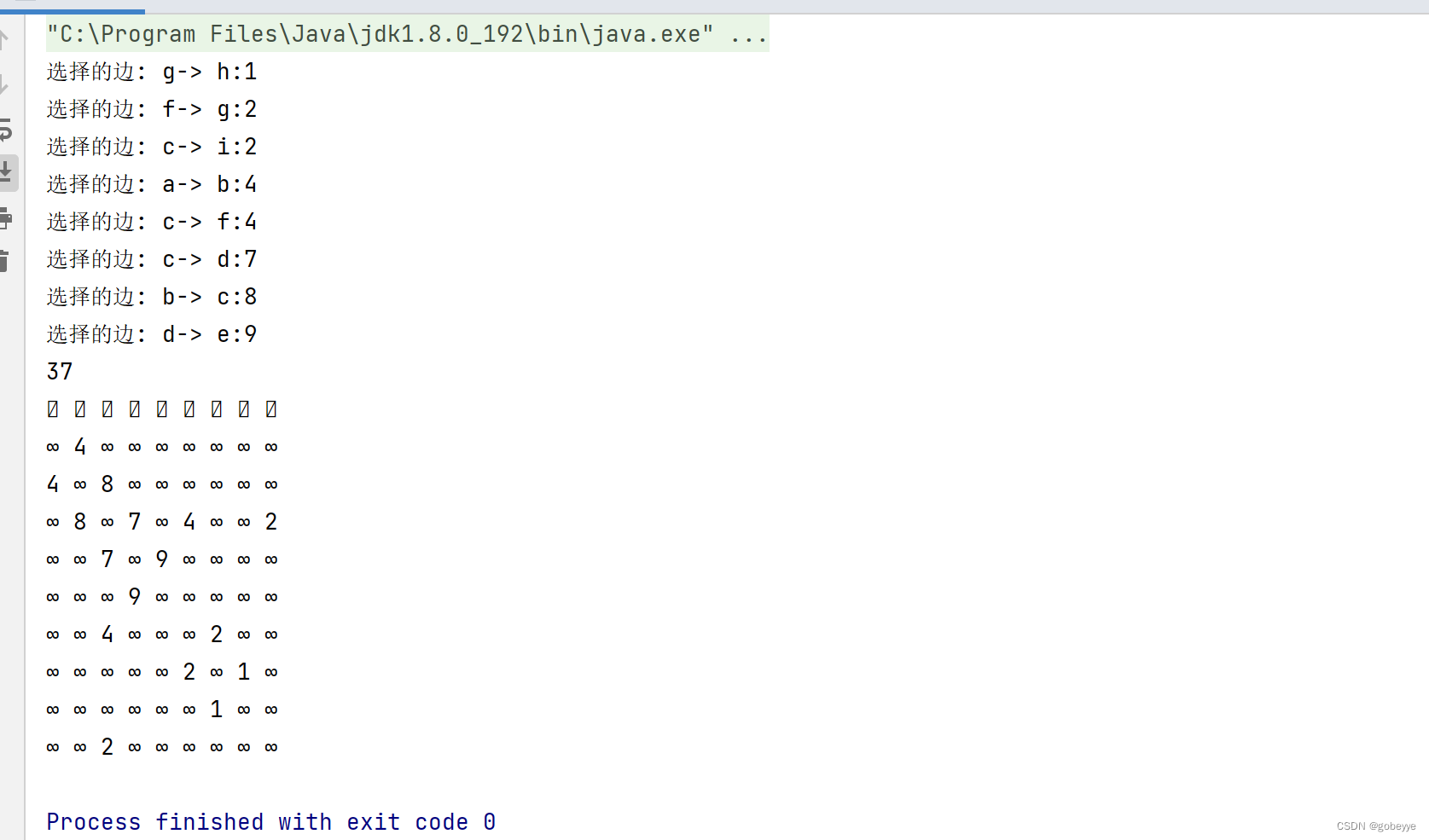
測試代碼：

public static void main(String[] args) {testGraphMinTreeKruskal();}public static void testGraphMinTreeKruskal() {String str = "abcdefghi";char[] array =str.toCharArray();GraphByMatrix g = new GraphByMatrix(str.length(),false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);//g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix  kminTree = new GraphByMatrix(str.length(),false);System.out.println(g.kruskal(kminTree));kminTree.printGraph();}

效果：

顯然正確💯

Prime算法：

Primel算法采用局部貪心的策略，其步驟如下：

按照字母順序abc....看。

代碼實現如下：

由于是局部貪心用兩個Set，那么天然就不會有環，故prime可以不用并查集。

1. 先獲取當前頂點的下標。

2. 定義一個X集合，把當前的起點下標存進去。

3. 定義一個Y集合，存儲目標頂點的元素。

4. 除了剛剛的起點，其他的頂點需要放到Y。

5. 從X集合中的點到Y集合的點中，連接的邊中找出最小值放到優先級隊列。

6. 把當前頂點連接出去的所有的邊放入隊列。

7.把這次的目標點，添加到X集合，變成了起點記得把之前的目標點，從Y集合刪除掉。

8.遍歷剛剛添加的新起點destIndex，連接出去的所有邊，再次添加到優先級隊列。

public int prim(GraphByMatrix minTree,char chV){//1. 先獲取當前頂點的下標int srcIndex = getIndexOfV(chV);int n = arrayV.length;//2. 定義一個X集合，把當前的起點下標存進去Set<Integer> setX = new HashSet<>();//3. 定義一個Y集合，存儲目標頂點的元素Set<Integer> setY = new HashSet<>();setX.add(srcIndex);//4. 除了剛剛的起點，其他的頂點需要放到Y集合for(int i = 0;i < n;i++){if(i != srcIndex){setY.add(i);}}//5. 從X集合中的點到Y集合的點中，連接的邊中找出最小值放到優先級隊列PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){@Overridepublic int compare(Edge o1,Edge o2){return o1.weight - o2.weight;}});//6. 把當前頂點連接出去的所有的邊放入隊列for(int i = 0;i < n;i++){if(matrix[srcIndex][i] != Integer.MAX_VALUE){minHeap.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));}}int size = 0;int totalWeight = 0;while(size < n - 1 && !minHeap.isEmpty()){//7. 取出隊列中的第一條邊Edge min = minHeap.poll();int srcI = min.srcIndex;int destI = min.destIndex;//起始點本身就在X集合，所以這里只需要判斷目標點即可if(setX.contains(destI)){//包含}else{//8. 直接將該邊 放入最小生成樹minTree.addEdgeUseIndex(srcI,destI,min.weight);//9. 每選一條邊 就打印一條語句System.out.println("選擇的邊: "+ arrayV[srcI] + "-> "+ arrayV[destI] + ":"+matrix[srcI][destI]);size++;totalWeight += min.weight;//10.把這次的目標點，添加到X集合，變成了起點setX.add(destI);//11.記得把之前的目標點，從Y集合刪除掉setY.remove(destI);//12. 遍歷剛剛添加的新起點destIndex，連接出去的所有邊，再次添加到優先級隊列for(int i = 0;i < n;i++){// 13. !setX.contains(i) 判斷目標點不能再X這個集合 例如: a->b 就包含了b->aif(matrix[destI][i] != Integer.MAX_VALUE && !setX.contains(i)){minHeap.offer(new Edge(destI,i,matrix[destI][i]));}}}}if(size == n-1){return totalWeight;}else{return -1;}}

測試：

測試對應的圖：

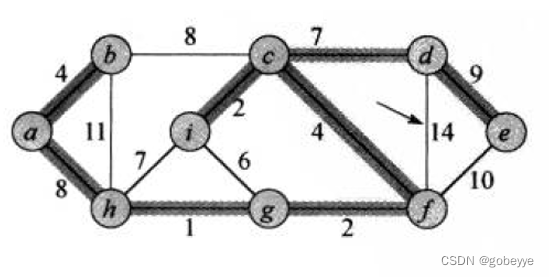
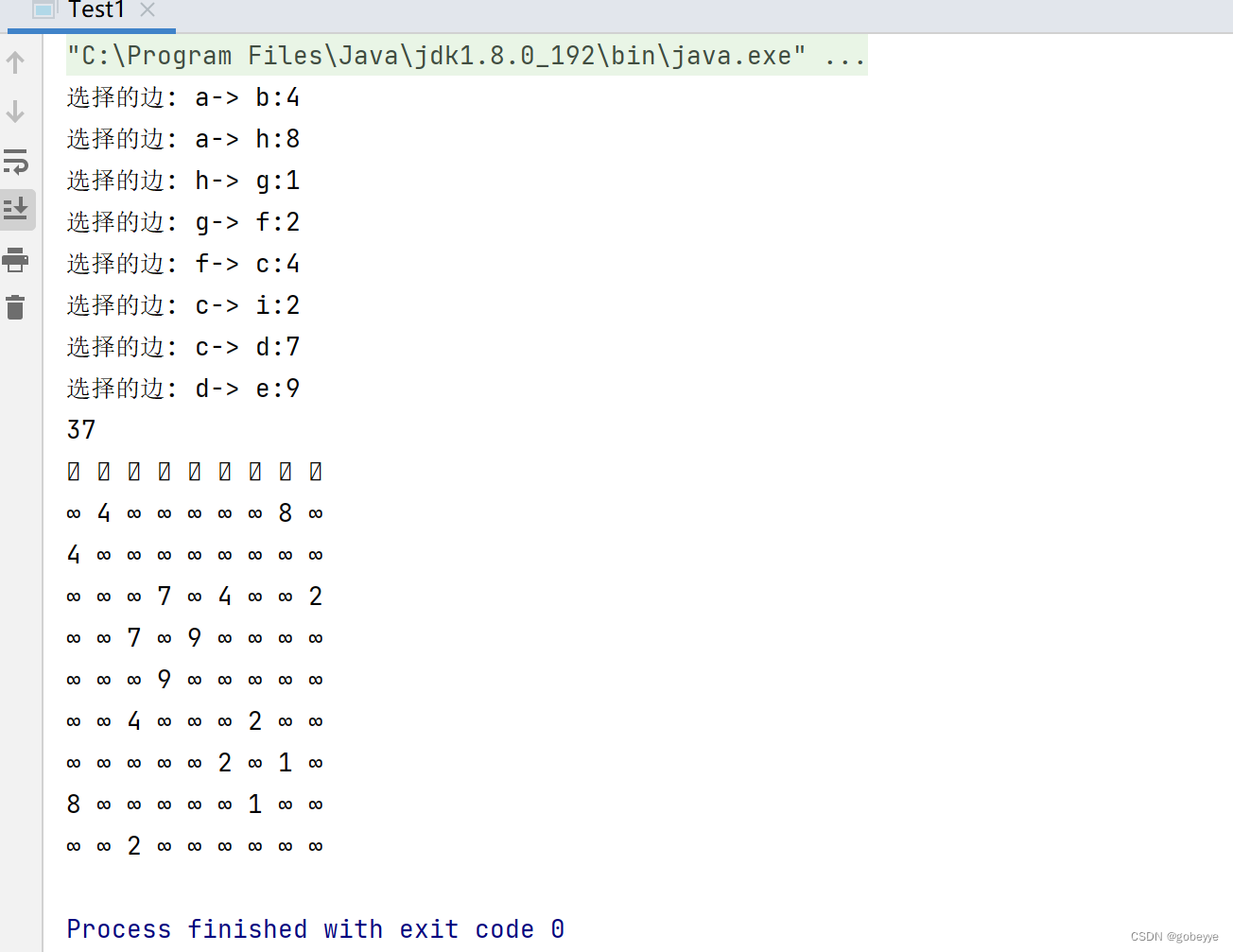
測試代碼：

public static void main(String[] args) {testGraphMinTreePrime();}public static void testGraphMinTreePrime() {String str = "abcdefghi";char[] array = str.toCharArray();GraphByMatrix g = new GraphByMatrix(str.length(), false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);//g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix primTree = new GraphByMatrix(str.length(), false);System.out.println(g.prim(primTree, 'a'));primTree.printGraph();}

效果：