Python 數據可視化之密度散點圖 Density Scatter Plot

🍉 CSDN 葉庭云：https://yetingyun.blog.csdn.net/

密度散點圖（Density Scatter Plot），也稱為密度點圖或核密度估計散點圖，是一種數據可視化技術，主要用于展示大量數據點在二維平面上的分布情況。與傳統散點圖相比，它使用顏色或陰影來表示數據點的密度，從而更直觀地展示數據的分布情況。密度散點圖能更好地揭示數據的集中趨勢和分布模式，尤其是在數據量非常大時，避免了散點圖中點重疊導致的可視化混亂問題。

在這里插入圖片描述

密度散點圖涉及的基礎概念：

散點圖（Scatter Plot）：基礎的二維數據表示形式，用于展示兩個變量之間的關系。每個數據點的位置由這兩個變量的值決定。當數據量龐大時，很多點會重疊在一起，使得無法清晰看到數據的分布。
核密度估計（Kernel Density Estimation，KDE）：一種用于估計隨機變量概率密度函數的非參數方法。通過平滑處理來填補單獨觀測值之間的空白，從而生成一個連續的概率密度函數。KDE 通常涉及到選擇一個核函數（如高斯核）和帶寬（控制平滑程度的參數）。
顏色編碼：在密度散點圖中，不同密度區域通常會使用不同顏色或深淺來表示，顏色深淺代表了該區域內數據點的密集程度。

可視化原理：

數據映射：首先將每個數據點映射到二維平面上。這與普通散點圖相同，這一步驟確定了每個點在圖上的位置。
密度估計：對所有數據點應用核密度估計算法。這一步驟是通過在每個數據點周圍放置一個“核”，然后對整個數據集覆蓋區域內所有核進行求和來完成的。結果是得到整個二維空間上每一位置的密度估計值。
顏色映射：根據得到的密度估計值為不同區域分配顏色或深淺。高密度區域將被賦予更深或更鮮艷的顏色，而低密度區域則使用較淺或較淡的顏色。
渲染顯示：最后將帶有顏色編碼的二維平面呈現出來，形成最終的密度散點圖。可選項：在繪制的密度散點圖的右方或下方展示顏色條 colorbar。

為什么要用密度散點圖？

探索數據分布：通過顏色編碼表示不同密度級別，密度散點圖能夠揭示出數據中可能隱含的各種模式、聚類或趨勢。這對于探索性數據分析尤其有用，因為它可以幫助研究人員發現未被預見到的關系或行為模式。我們可以看到哪些區域有更密集的數據點，哪些區域相對稀疏。在處理包含上萬個數據點的大型數據集時，傳統散點圖可能會導致嚴重的過度繪制（overplotting），即不同數據點在圖表上的位置重疊，使得無法清晰地看到數據分布。密度散點圖通過表示區域內數據點的相對密度來解決這個問題，從而提供了一種更清晰、更有效地理解數據分布的方式。
優化視覺呈現：密度散點圖通過采用漸變色或色階映射等方法，幫助清晰地展示數據，相比傳統散點圖的混亂和模糊。這樣可以更容易區分高密度和低密度區域，使整體呈現更美觀、易于理解。高靈活性的密度散點圖支持多種定制選項，比如調整顏色映射、透明度、標記大小等，以適應不同類型和規模的數據集。此外，還可以結合其他類型的可視化技術（比如輪廓線或網格）來增強表達能力。
異常值檢測：密度散點圖可以幫助我們識別異常值。如果某個區域的密度遠高于其他區域，那么可能存在異常值。
聚類分析：密度散點圖可以幫助我們發現數據的聚集區域。如果某個區域有較高的密度，那么這可能是一個數據聚類的中心。
模型預測結果分析：密度散點圖非常適合用于可視化觀測值和擬合值的情況，能觀察到模型預測的潛在偏移與合理性。
促進決策制定：在商業智能、金融分析、生物統計等領域，了解和分析復雜數據集中的模式對于指導決策至關重要。密度散點圖提供了一種直觀方法來識別關鍵變量之間的關系和動態變化，從而幫助決策者基于深入洞察做出更加明智的選擇。

總結來說，使用密度散點圖在處理大規模和 $/$ 或復雜數據集時提供了一種極具價值的工具。它不僅能夠有效解決過度繪制問題，還能揭示出隱藏在龐大數據背后的結構和模式，同時提供優雅且功能強大的視覺展示方式。無論是在科研、工業還是商業領域，掌握并應用這種技術都將極大地增強對數據的理解和利用能力。

下面講解一個帶擬合曲線的密度散點圖的繪圖示例。

導入需要的依賴庫：

import numpy as np
from numpy import polyfit, poly1d
import matplotlib as mpl
from matplotlib import cm
from matplotlib import ticker
from matplotlib import colors
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from scipy.stats import gaussian_kde

繪制帶擬合曲線的密度散點圖的 Python 代碼如下：

# 固定 numpy 的隨機種子
np.random.seed(2024)# 構造二維數據 x 和 y
x = np.random.normal(loc=0.0, scale=1.0, size=1000)
y = x + np.random.normal(loc=0.1, scale=1.0, size=1000)# 核密度估計
x_and_y = np.vstack([x, y])
kde = gaussian_kde(x_and_y)
z = kde(x_and_y)
idx = z.argsort()
x, y, z = x[idx], y[idx], z[idx]is_cbar = True# 創建圖形和坐標軸
fig, ax = plt.subplots(figsize=(7, 4), dpi=150)# cmap: bwr、Spectral_r、viridis_r、spring、gist_rainbow_r、RdBu_r
# 可設置的 colormaps - https://matplotlib.org/tutorials/colors/colormaps.html
my_cmap = "bwr"# 繪制密度散點圖
ax.scatter(x, y, c=z, cmap=my_cmap)# 用 7 次多項式擬合，調用 poly1d 方法得到多項式系數。
y_fit = polyfit(x, y, 7)
y_fit_1d = np.poly1d(y_fit)
y_hat = np.polyval(y_fit, x)# 計算相關系數和 R^2
print('Correlation coefficients：')
print(np.corrcoef(y_hat, y))
correlation = np.corrcoef(y_hat, y)[0, 1]
R_square = correlation ** 2
print("R^2：", R_square)xtick = np.linspace(min(x), max(x), 1000)
# 擬合的多項式曲線
plt.plot(xtick, y_fit_1d(xtick), color="#FF0066", lw=2.2)# 坐標軸刻度的數值使用 Latin Modern Math 字體
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontproperties(font_latex2) for label in labels]
[label.set_color('black') for label in labels]# 設置坐標軸刻度
plt.tick_params(axis='x', direction='out', labelsize=13, length=4.6, width=1.15)
plt.tick_params(axis='y', direction='out', labelsize=13, length=4.6, width=1.15)# 展示 X 和 Y 軸的子刻度
ax.xaxis.set_minor_locator(ticker.AutoMinorLocator())
ax.yaxis.set_minor_locator(ticker.AutoMinorLocator())# 顏色條的設置：刻度、字體、字號等
if is_cbar:norm = colors.Normalize(vmin=np.min(z), vmax=np.max(z))cbar = plt.colorbar(cm.ScalarMappable(norm=norm, cmap=my_cmap), ax=ax)cbar.ax.set_ylabel("Density", fontproperties=font_latex2, labelpad=12)cbar.ax.tick_params(labelsize=12)labels = cbar.ax.get_xticklabels() + cbar.ax.get_yticklabels()[label.set_fontproperties(font_latex2) for label in labels][label.set_color('black') for label in labels]tick_locator = ticker.MaxNLocator(nbins=8)cbar.locator = tick_locatorcbar.update_ticks()# 設置 X 軸和 Y 軸的刻度值范圍
ax.set_xlim(left=-6, right=6.0000001)
ax.set_xticks(np.arange(-6, 6.000001, step=2.0))
ax.set_ylim(bottom=-6, top=6.0000001)
ax.set_yticks(np.arange(-6, 6.000001, step=2.0))# 畫圖對象周圍的框的加粗一點
lw = 1.25
ax.spines["right"].set_linewidth(lw)
ax.spines["left"].set_linewidth(lw)
ax.spines["top"].set_linewidth(lw)
ax.spines["bottom"].set_linewidth(lw)# 設置 X 軸和 Y 軸的標簽、字體、刻度和刻度標簽在內的坐標軸邊界框中的間距
plt.xlabel("X Label", fontproperties=font_latex1, labelpad=8)
plt.ylabel("Y Label", fontproperties=font_latex1, labelpad=8)# 設置標題 字體 大小 以及距繪圖對象的距離
plt.title("Python Matplotlib - Density Scatter Plot",fontproperties=font_latex2, pad=12)# 文本的位置是根據數據坐標來確定的
ax.text(x=-5, y=4.5, s=r'$\ {R^2} = 0.522$', usetex=True,fontsize=14, fontweight="bold")# 顯示網格  虛線和透明度
plt.grid(alpha=0.360, ls="--", which="major", color="#A9A9A9")
# 緊湊布局
plt.tight_layout()plt.savefig("./Figures/密度散點圖.png", dpi=300, bbox_inches="tight")
plt.show()

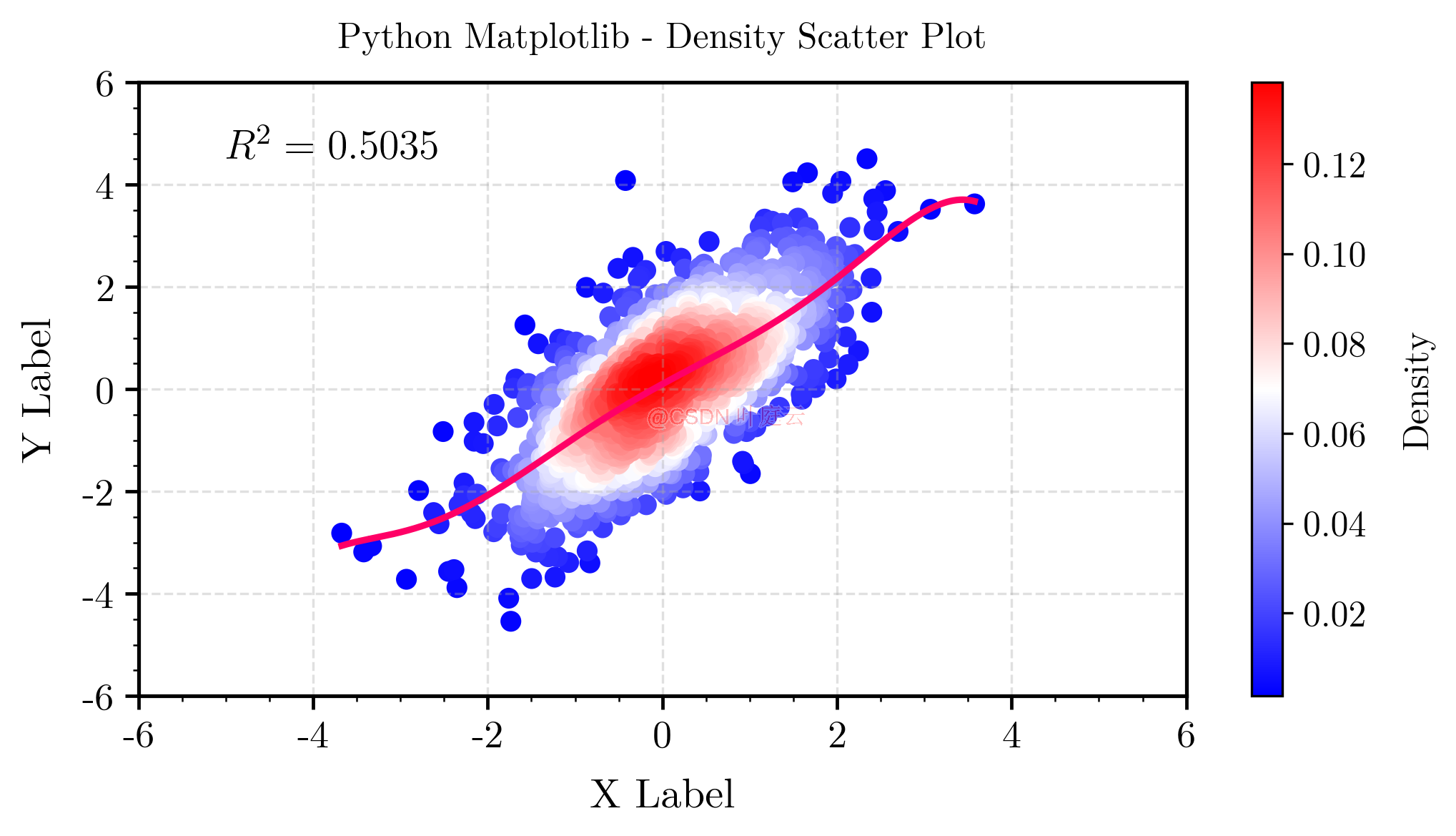
整體解釋：這段代碼首先導入了所需的庫，然后生成了測試數據 $x$ 和 $y$ （實際應用還可能是真實值 $y$ 和預測值 $\hat y$ ）。接著，它使用核密度估計（KDE）來計算數據的密度分布。之后，它繪制了一個密度散點圖，并使用多項式擬合來生成一個曲線。最后，它計算了相關系數和 $R^2$ 值，并設置了各種圖形屬性，如坐標軸刻度、顏色條、網格等。最后，它將圖像保存為一個 .png 文件并顯示出來。