
 來源 | 碼海責編 | Carol封圖 |?CSDN 付費下載于視覺中國我們幾乎每天都在用搜索引擎搜索信息,相信大家肯定有注意過這樣一個細節:當輸入某個字符的時候,搜索引框底下會出現多個推薦詞,如下,輸入「python」后,底下會出現挺多以python 為前綴的推薦搜索文本,它是如何實現的呢?
來源 | 碼海責編 | Carol封圖 |?CSDN 付費下載于視覺中國我們幾乎每天都在用搜索引擎搜索信息,相信大家肯定有注意過這樣一個細節:當輸入某個字符的時候,搜索引框底下會出現多個推薦詞,如下,輸入「python」后,底下會出現挺多以python 為前綴的推薦搜索文本,它是如何實現的呢?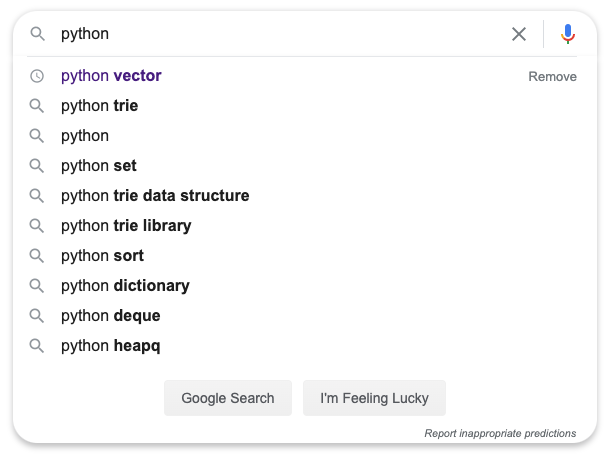
- 什么是 Trie 樹
- Trie 樹的實現
- 如何實現搜索字符串自動提示
- 再談 Trie 樹

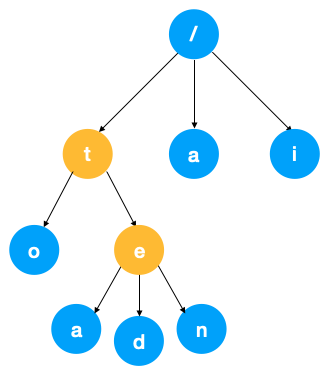
- 根節點不包含字符,除根節點外每個節點只包含一個字符
- 從根節點到某一節點,路徑上經過的字符連接起來,為該節點對應的字符串。如上圖中從根節點到結點 o,經過的字符為「t」和「o」,所以它表示單詞 to。
- 每個節點的所有子節點包含的字符都不相同,這一點也就保證了相同的前綴能夠得到復用。

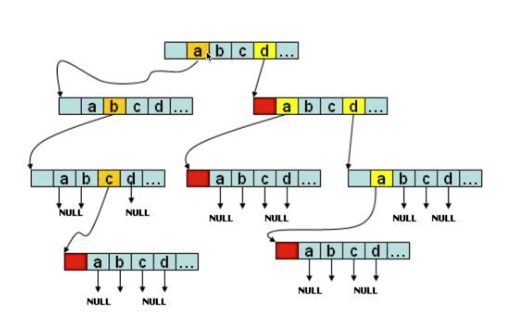
/**
?*?26?個字母
?*/static?final?int?ALPHABET_SIZE?=?26;/**
?*?Trie?樹的節點表示
?*/static?class?TriedNode?{/**
?????*?根節點專用,存儲?"/"
?????*/public?char?val;/**
?????*?以此結點字符為終止字符的字符串的個數
?????*/public?int?frequency;/**
?????*?節點指向的子節點
?????*/
????TriedNode[]?children?=?new?TriedNode[ALPHABET_SIZE];public?TriedNode(char?val)?{this.val?=?val;
????}
}/**
?*?Trie?樹
?*/static?class?TrieTree?{private?TriedNode?root?=?new?TriedNode('/');?//?根節點
}- 根據一組字符串構造 Trie 樹
- 在 Trie 樹中查找字符串是否存在
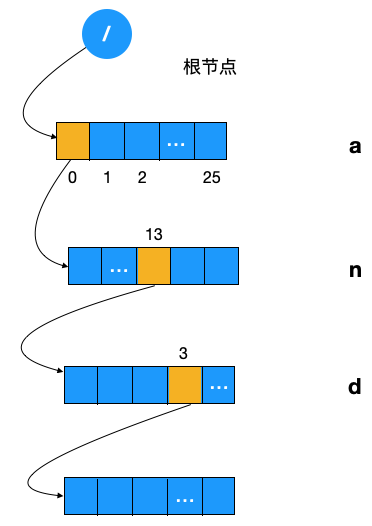
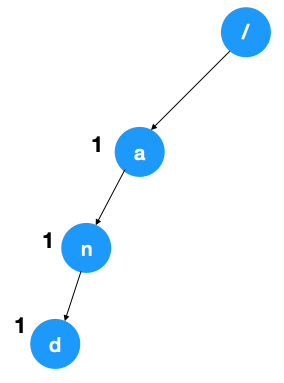
- 構建根節點,此時根節點存有一個元素大小為 26 的數組
- 遍歷字符串「and」
- 遍歷第一個字符 a 時,將上述數組的第一個元素賦值為一個 TriedNode 實例(假設其名為 A)
- 當遍歷第二個字符 n 時,將 A 結點 TriedNode 數組下標為 n-a = 13 (a 的 ascii 為 97,n 的 ascii 碼為 110) 的元素賦值為一個 TriedNode 實例(假設其名為 N)
- 同理,當遍歷第三個字符 d 時,將 N 結點 TriedNode 數組的第 4 個元素(下標為 3)賦值為一個 TriedNode 實例(假設其名為 D),同時也將其結點的 frequency 加一,代表以此字符為終止字符的字符串多了一個。
/**
?*?Trie?樹
?*/static?class?TrieTree?{private?TriedNode?root?=?new?TriedNode('/');?//?根節點/**
?????*?以?String?為條件構建?Trie?樹
?????*?@param?s
?????*/public?void?insertString(String?s)?{
????????TriedNode?p?=?root;for?(int?i?=?0;?i?????????????char?c?=?s.charAt(i);int?index??=?c-'a';if?(p.children[index]?==?null)?{
????????????????p.children[index]?=?new?TriedNode(c);
????????????}
????????????p?=?p.children[index];//Process?char
????????}
????????p.frequency++;
????}
}/**
?*?查找字符串是否在原字符串集合中
?*?@param?s
?*?@return?boolean
?*/public?boolean?findStr(String?s)?{
????TriedNode?p?=?root;for?(int?i?=?0;?i?????????//?當前被遍歷的字符char?c?=?s.charAt(i);int?index??=?c-'a';if?(p.children[index]?==?null)?{//?如果字符對應位置的數組元素為空,說明肯定不存在此字符,終止之后的字符遍歷return?false;
????????}//?如果存在,則繼續往后遍歷字符串
????????p?=?p.children[index];
????}return?true;
}
如何實現搜索字符串自動提示功能
有了 Trie 樹,相信大家不難解決開篇的這個問題,首先搜索引擎根據用戶的搜索詞構建一顆 Trie 樹,假設這個搜索詞庫是 a, to, tea, ted, ten, i, in, inn,則構建的 Trie 樹為:
- 先根據用戶輸入的前綴在樹中找出含有此前綴的所有字符串
- 我們知道在節點中保存了字符串的被搜索次數,所以利用小頂堆即可算出被搜索次數最多的 10 個字符串,即可得最終展示給用戶的提示詞。
這樣就解決了,考慮以下現象:我們在輸入搜索詞的時候,搜索引擎給出的提示詞可能并不是以用戶輸入的字符串為前綴的。
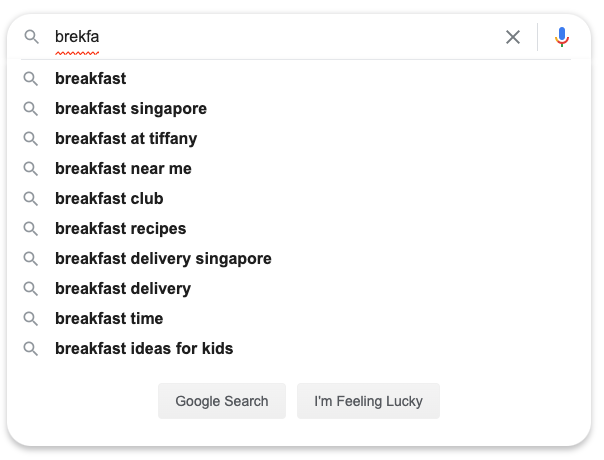
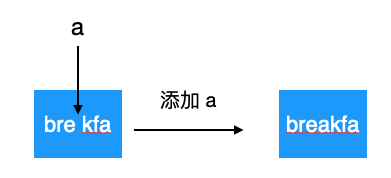
這種又是怎么實現的呢,它實際上用到了字符串編輯距離的思想,所謂字符串編輯距離是說一個字符串可以通過增刪改查字符來變成另外一個字符串。

再談 Trie 樹
從前面的介紹中我們可以看到使用 Trie 樹確實在能在快速查找字符串與詞頻統計上發揮重要作用,但天下沒有免費的午餐,如果字符集比較大的話,用 Trie 樹可能會造成空間的浪費,以上文中構建的 Trie 樹為例
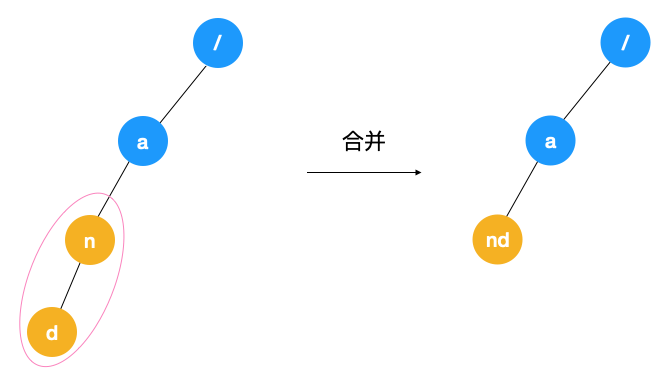
如果是字符串的精確匹配查找,我們一般建議使用散列表或紅黑樹來解決,畢竟很多語言的類庫都有現成的,不需要自己實現,拿來即用
如果需要進行前綴匹配查找,則用 Trie 樹更合適一些

總結
本文通過搜索引擎字符串提示簡要地概述了其實現原理,相信大家應該理解了,需要注意的是其使用場景,更推薦在需要前綴匹配查找的時候用 Trie 樹,否則像一般的精確匹配查找等更推薦用散列表和紅黑樹這些很成熟的數據結構,畢竟這兩數據結構實現一般在類庫中都是實現了的,不需要自己實現,盡量不要重復造輪子。
 推薦閱讀
推薦閱讀手把手教你配置VS Code 遠程開發工具,工作效率提升N倍
用大白話徹底搞懂HBase RowKey詳細設計
后端程序員必備:書寫高質量SQL的30條建議
Go 遠超 Python,機器學習人才極度稀缺,全球 16,655 位程序員告訴你這些真相!
任正非談“狼文化”:華為沒有 996,更沒有 007
區塊鏈必讀“上鏈”哲學:“胖鏈下”與“瘦鏈上”
在商業中,如何與人工智能建立共生關系?

)的輸出結果是)

...)
 如何用Apache POI操作Excel文件-----POI-3.10的一個和注解(comment)相關的另外一個bug...)

)




)

)




:MySQL服務安裝實戰)
