基本思想
希爾排序(Shell's Sort),以發明人命名,又稱為縮小增量排序,也是一種插入排序算法。
主要思想:直接插入排序算法時間和待排數據有關,其平均復雜度是O(n^2),但是在待排數據已經有序的情況下,其復雜度可以達到O(n),因為不需要移動數據。
希爾排序就是利用這種特點,先將整個待排數據記錄分割成若干個子待排數據記錄,然后分別進行直接插入排序,當整個待排數據記錄“基本有序”時,再對整個數據記錄進行完整的一次直接插入排序。通俗地來說,先“跳著”給待排序列排序幾個數據,讓待排數據基本有序的情況,再直接插入排序。
舉例來說:
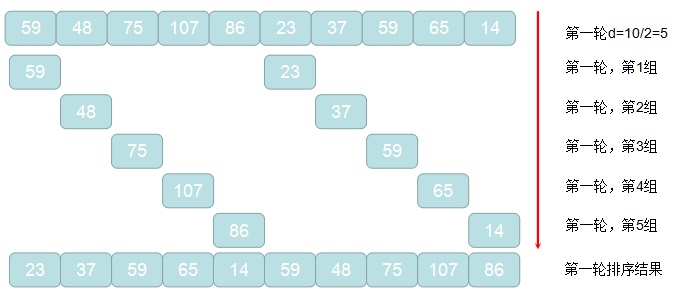
例如:給定10個整數:(4,3,1,2,6,5,0,9,8,7) 從小到大排序。
第一步:
假定先分成五個子序列,請注意增量分割,例如第1個元素和第6個元素是一個子序列,第2個元素和第7個元素是一個子序列。最終分成 (4,5)(3,0)(1,9)(2,8)(6,7),對子序列分別排序,最終得到結果:
(4,0,1,2,6,5,3,9,8,7),調整了(3,0)的位置。
第二步:
分成三個子序列,縮小增量,因此第1個元素和第4個元素、第7個元素、第10個元素是一個子序列。最終分成(4,2,3,7)(0,6,9)(1,5,8),同樣對子序列的數據進行排序,得到結果:(2,3,4,7)(0,6,9)(1,5,8),最終得到:
(2,0,1,3,6,5,4,9,8,7)
第三步:
分成一個子序列,也就是增量為1,此時和直接插入排序一樣,對整個序列進行直接插入排序即可。
算法有效的特征時:使用增量分割序列時,有可能會讓“亂序”的數據“跳躍到”前面,這樣不用移動位置,從而減少移動的次數。
希爾排序算法時間復雜度分析是個復雜的難題,其針對每個隊列的所選的增量序列不同,時間不同。增量序列的值應滿足沒有除1以外的公因子,并且最后一個增量值為1,例如......11,9,5,3,2,1等。
代碼實現
希爾排序與直接插入排序相比:
1.需要進行多次子排序過程,每次子排序也是直接插入排序。
2.需要一個增量序列,分割整個待排序列。
/*
#include <stdio.h>// 對分割每個子序列進行排序
// dk比較子序列增量
void shell_insert(int a[], int length, int dk)
{int i,j,t;for(i=dk; i<length; i++){if(a[i] < a[i-dk] ){t = a[i];for(j=i-dk; j>=0 && t < a[j]; j=j-dk)a[j+dk] = a[j];a[j+dk] = t;}}
}void shell_insert_sort(int a[], int length, int dk[], int dk_length)
{int i;for(i=0; i<dk_length; i++){shell_insert(a, length, dk[i]);}
}
int main(void)
{int a[10] = {4,3,1,2,6,5,0,9,8,7};int dk[3] = {5,3,1};shell_insert_sort(a,10,dk,3);int i;for(i=0; i<10; i++)printf("%d ", a[i]);return 0;
}
其實做為一個學習者,有一個學習的氛圍跟一個交流圈子特別重要這里我推薦一個C/C++基礎交流583650410,不管你是小白還是轉行人士歡迎入駐,大家一起交流成長。



















)
