幫助你理解線性代數與機器學習緊密結合的核心內容

下文節選自北大出版社《機器學習線性代數基礎》, [遇見]已獲授權許可. 這本書不同于傳統教材, 從新的角度來介紹線性代數的核心知識, 講解也很棒, 又剛好參加參加了當當每滿100-50的活動, 感興趣的朋友可以關注下.?

傅里葉級數：從向量的角度看函數

本節將采用一種全新的視角去看待函數，把函數看作是無窮維向量空間中的一個向量。這樣，我們就能引入??維向量空間??中的許多運算法則，其中一個重要的運算就是向量的內積。通過概念的類比，對兩個函數的內積運算和正交性進行定義，并參照向量中標準正交基的相關概念，引入通過一組正交基函數對一個連續函數進行分解的方法。在這種思想方法的引領下，本節從向量的視角去介紹和講解函數的傅里葉分析方法，介紹由正余弦函數組成的正交函數基，以及周期函數的傅里葉級數求解方法，本節可以看作是線性代數理論和工具向函數空間的拓展，仔細分析會發現向量與函數的一些思想方法的共通之處。

1. 函數：無窮維向量

空間是整個線性代數理論與實踐的核心概念，下面先簡要地回顧一下向量空間的有關概念。向量空間??由所有含有??個成分的列向量所構成。例如，??空間中就包含了所有含有??個成分的列向量?， 因此??空間也稱為是??維空間，在這個向量空間??中，還定義了向量的加法、標量乘法以及內積等基本運算法則。在這里需要說明的是，我們一直所討論的向量空間??是一個有限維的空間，即向量中的成分個數是有限的。而接下來，我們會把思路進一步的打開，將空間的概念從狹義引申到廣義，去探討一下函數和向量之間的關聯。函數的概念相信讀者并不會感到陌生，函數反映的是自變量和因變量之間的一種映射關系，如果給定自變量元素?，對他施加映射規則?，就得到了因變量元素?，即我們所熟悉的表示方法：?。這種看待問題的角度來源于函數的基本定義，但是從中我們似乎找不到函數和向量有什么關聯。這是因為從解析式的角度去看待函數，關注的是它的映射規則。如果從更直接的角度去看待呢？回顧一下繪制一條函數曲線的過程，我們會對應地在坐標系中對各個自變量的取值進行描點，然后將這些點連接成函數曲線。我們會發現：如果自變量的取值越密集，那么所描繪出來的曲線就越趨近于原始的函數曲線，當??的時候，通過描點法繪制出來的曲線就和真實的函數曲線無異了。此時，如果對函數曲線依照??的間隔進行均勻采樣，如圖 7.1 所示，就能得到一組采樣值?，特別地，當采樣間隔??的時候，這一組采樣值就能夠完全地代表這個函數了。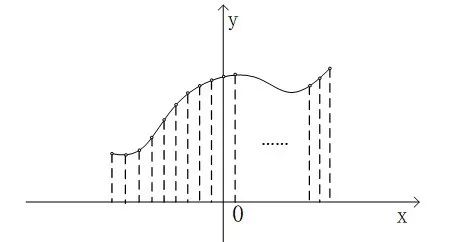

圖1. 對連續函數曲線按 的間隔均勻采樣?此時，如果利用向量工具對這一組函數值進行表示，即表示為?，它就和函數很自然的對應了起來，這是一種返璞歸真的思路和方法。并且最為重要的一點是，由于自變量??和??之間的間距?，因此采樣的個數，即向量中的成分個數是無限的，由此又可以說：我們成功的把函數放到了一個無窮維的向量空間當中去了。建立起了這種對應關系后，就可以采用向量空間中介紹過的運算法則和相關概念，來進一步討論構建在空間中的函數運算性質。

2. 尋找一組正交的基函數

一旦將函數看作是無窮維空間中的向量，那么自然而然的就可以將??維向量空間??中的內積定義進行遷移。向量的坐標基于基底的選取，向量空間??中的任何一個??維向量??都可以寫成??個基向量??線性組合的形式，即：??，并且這種表示方法是唯一的，我們在此基礎上對向量進行進一步的變換和分析。如果從向量的角度去審視函數，我們能否將一個指定的函數??寫成一組基函數的組合呢？答案是肯定的，并且正如同基向量的選取有很多種選擇一樣，基函數也有不同的多種選擇，那么什么樣的基函數才能稱得上是好的基函數呢？關于這一點，我們同樣去從向量空間中尋找答案。在向量空間中，標準正交向量滿足彼此無關，且同時滿足向量為單位長度的特性，一般使用一組標準正交向量作為基向量，它們性質優越、操作簡便。我們以此類推，是否也應該選取類似性質的一組函數作為??在無窮維向量空間中的基函數呢？答案是肯定的，下面就讓我們按照這個思路去尋找和討論。驗證兩個向量是否滿足正交，需要進行的是向量的內積運算，回顧一下兩個??維向量??和??進行內積運算的運算法則：???如果要滿足向量??和向量??之間彼此正交，則他們的內積運算結果必須為 0，即：。那么兩個函數??和??的內積該如何進行表示呢？很顯然，由于他們被表示成了向量，直觀上看函數的內積表示形式同向量相比應該是一樣的，但是在這里我們需要注意兩個要點：一方面是參與內積運算的兩個向量的維數都是無窮的；另一方面它們的采樣間隔都是趨近于 0。因此很自然，離散量的加和運算演變成了連續量的積分運算，兩個無窮維向量的內積運算本質上就是兩個函數乘積的積分(這是微積分里的基本概念，相信讀者不會感到陌生)，因此，我們可以將函數??和??的內積表示成：??如果積分運算的結果為 0，則表示這兩個函數滿足彼此正交的關系，即有希望被我們選擇作為基函數。下面來看一個實際的例子，計算一下我們熟悉的正弦函數??和余弦函數??的內積，由于他們都是周期為??函數，因此我們計算??范圍內的積分結果：代碼如下：

from sympy import integrate, cos, sinfrom sympy.abc import ximport numpy as npe = integrate(sin(x)*cos(x), (x, 0, 2*np.pi))print(e.evalf())br

運行結果：

0

從代碼的運行結果中我們可以看到：積分運算的結果為 0，即兩個函數的內積為 0，說明他們彼此之間是滿足正交的，這個結果正如我們所期待。但是，僅僅由正弦函數??和余弦函數??作為基函數是遠遠不夠的，因為從基向量的相關概念中我們知道，?維向量空間??中的任意一個向量都被表示為空間中??個基向量的線性組合形式，而我們將函數視作是無窮維的向量，因此通過類比可知，我們需要的不是兩個基函數，而是一組滿足彼此之間兩兩正交的無窮序列作為基函數。正弦函數和余弦函數的正交性不僅僅局限在??和??這兩個函數，實質上，下面這個正余弦函數的無窮序列兩兩之間都滿足正交性：??類似地，這種無窮序列正是我們想要的，他是針對函數這個無窮維向量的一組好基。和 滿足正交性的推演過程并不難，也是通過驗證二者的乘積在 取值范圍內的積分是否為 0，具體的計算過程我們就不在這里展開了，幾個實例演算代碼請見書中所示。通過程序的運行結果，確實該序列中的函數兩兩之間滿足正交的關系。當然了，滿足彼此正交的基函數不僅僅只有這一種。

3. 周期函數與傅里葉級數

函數可以分為周期函數和非周期函數兩個大類，首先從周期函數入手去展開討論，首先我們從一個指定周期為??的函數??開始進行分析，這是最基本、最典型的一種情況。有了這組由正余弦函數無窮序列所構成的正交基函數，我們就可以按照之前的思路對函數??進行處理，在無窮維的空間中，在正余弦函數所構成的基上進行函數展開，將函數??寫成他們的線性組合的形式：?接著把上面的式子寫成展開式的形式：?這種級數的展開形式就是周期為??的函數??的傅里葉級數，這里有幾點需要注意一下：第一：從展開式中我們可以看出，周期為??的函數??被表示成了正弦函數??和余弦函數??所構成的基函數的線性組合，并且在通常的情況下，基函數的個數是無窮多個。第二：我們確實是實現了我們制定的重大目標，這一組基函數是彼此正交的。第三：按照傅里葉級數對函數 進行展開的操作，其物理意義是非常重大的。如果我們把函數??的自變量??替換成?，可能大家會更加豁然開朗。?，我們利用這個等式建立起了時域和頻域的橋梁，等式的左側是關于時間 的函數，而右側則是一系列不同頻率諧波的疊加，且這些諧波的頻率都是周期函數??頻率的整數倍。通過傅里葉級數，很巧妙的拿到了周期函數用不同頻率諧波疊加的表達方式，這樣就可以非常直觀的去除掉某個指定頻率的成分，這在信號處理的領域中是最為重要也最為基礎的概念。如果我們僅僅是去觀察時域中的函數曲線?，想要實現上述的濾波功能，看似是根本不可能的，而一旦通過傅里葉級數將時域函數??轉換到頻域當中，這個濾波的過程就變得相當簡單了。關于傅里葉級數的應用我們也就點到為止，如果讀者感興趣，可以去查閱信號處理的相關資料。更一般地，如果時域中的函數??是任意周期?，那么我們用于傅里葉級數展開的基頻率就是?(在前面周期為??的例子中，基頻率就是?)，傅里葉級數中所有正余弦函數的頻率都是基頻率的整數倍，依次為：。最終，對于周期為??的時域函數?，對他的傅里葉級數進行一般化的描述，就記作為：?

4. 傅里葉級數中的系數

通過??這個重要的式子，我們架起了時域和頻域之間的聯通橋梁，從一個隨著時間??不斷變化的函數曲線中提取出了他的頻譜。傅里葉級數中的??等稱之為傅里葉系數，它反映了各個用來疊加的諧波幅度，體現了各個頻率分量在總的信號中所占的分量。這種級數展開的形式其實在我們這本書的介紹中前前后后已經出現了好幾次，并且都是非常重要的關鍵點，本質上都是將待處理的對象進行分解，將其轉換到一組選定的正交基上，并且用一些指標來衡量各個正交基所代表成分的重要性程度。我們一起來回憶一下前面出現過的幾種類似情況：(1)在主成分分析的過程中，我們選取的正交基是數據協方差矩陣??的??個標準正交特征向量，我們利用特征向量所對應的特征值來衡量他們的優先順序；(2)在利用奇異值分解進行數據壓縮的過程中，我們把待壓縮的數據矩陣寫成??的形式，其中展開式里每一個??相乘的結果都是一個等維的?形狀的矩陣，并且它們彼此之間都滿足相互正交的關系，前面的系數??則是各個對應矩陣的權重值。??的不等關系則依序代表了各個矩陣片段“重要性”的程度；我們把待分析的對象分解到了一組基上，這些基的具體形態各異，它們可以是向量，可以是矩陣，也可以是函數，而這些基因為相互正交而彼此無關，這些彼此無關的成分由于其擁有不同的權重，因此提供給了我們處理具體問題的量化依據。正因為如此，求取傅里葉級數的系數就顯得非常重要，表面上看我們的已知信息并不多，而級數卻又是無窮級數，那么這應該如何處理呢？實際上，只需要抓住各個基函數彼此之間滿足正交的特性就可以很容易的進行處理了，傅里葉級數??中的各項除了與自身以外，與其他各項都保持正交，依據此項特性，對于任意系數??而言，我們有：同理，對于系數 而言同樣有：?這里的積分運算并不太難，我們就不具體推演了，最后我們直接給出傅里葉級數系數的表達式：由此，我們就求得了傅里葉級數的各個系數。

5. 非周期函數與傅里葉變換

討論完了周期函數，再來介紹非周期函數的情況。在周期函數的傅里葉級數中與函數周期??密切相關的量就是基頻率?，基函數中任意一個正余弦函數的頻率都是他的整數倍，這個我們之前已經講過，換句話說，?表示的就是從時域轉換到頻域之后，頻譜中各相鄰頻率的間隔。而我們可以把非周期函數看做是周期??無窮大的周期函數，因此，頻率間隔?，譜線越來越密，最終由離散譜變成了連續譜。

6. 思維拓展分析

其實傅里葉分析的具體細節遠遠不止這些，想要更深入、更細致的掌握他還需要花些功夫，當然這些細節并不是我們本書的核心重點。本節主要目的是對我們的思維進行拓展，把線性代數的一些運算方法和處理思想從傳統的向量空間拓展到無窮維的函數空間中去。通過把向量的內積、正交等運算概念進行類比引入，實現對正交的函數基的概念定義和方法運用，巧妙的連接起時域和頻域，這非常有助于我們去體會向量與函數的共通之處。

向上滑動閱覽簡介及目錄?

本書以機器學習涉及的線性代數核心知識為重點，進行新的嘗試和突破：從坐標與變換、空間與映射、近似與擬合、相似與特征、降維與壓縮這5個維度，環環相扣地展開線性代數與機器學習算法緊密結合的核心內容。?

第1章 坐標與變換：高樓平地起
1.1描述空間的工具：向量 2
1.2基底構建一切，基底決定坐標 13
1.3矩陣，讓向量動起來 18
1.4矩陣乘向量的新視角：變換基底 27
　第2章 空間與映射：矩陣的靈魂
2.1矩陣：描述空間中的映射 34
2.2追因溯源：逆矩陣和逆映射 42
2.3向量空間和子空間 50
2.4老樹開新花，道破方程組的解 55
　第3章 近似與擬合：真相*近處
3.1投影，尋找距離*近的向量 62
3.2深入剖析*小二乘法的本質 69
3.3施密特正交化：尋找**投影基 74
　第4章 相似與特征：**觀察角
4.1相似變換：不同的視角，同一個變換 80
4.2對角化：尋找*簡明的相似矩陣 85
4.3關鍵要素：特征向量與特征值 89
　第5章 降維與壓縮：抓住主成分
5.1*重要的矩陣：對稱矩陣 96
5.2數據分布的度量 100
5.3利用特征值分解(EVD)進行主成分分析(PCA) 103
5.4更通用的利器：奇異值分解(SVD) 111
5.5利用奇異值分解進行數據降維 116
　第6章 實踐與應用：線代用起來
6.1SVD在推薦系統中的應用 124
6.2利用SVD進行彩色圖片壓縮 133
　第7章 函數與復數域：概念的延伸
7.1傅里葉級數：從向量的角度看函數 145
7.2復數域中的向量和矩陣 151