大鳳號裝甲空母
時間限制: 1 Sec 內存限制: 128 MB
提交: 108 解決: 15
[提交] [狀態] [命題人:admin]
題目描述
大鳳號航空母艦很喜歡算術。
它，是舊日本海軍中最為先進的航空母艦。
它，是舊日本海軍中最為短命的航空母艦。
同時，她還是最平的航空母艦（龍驤：你說啥？）
如此多第一 ……
一生二，二生三，三生萬物 ……
這也許就是大鳳喜歡算術的原因吧。
有一天，她看到了這樣一道題：
令
電探發現了來自遠處的魚雷，時間不多了。

輸入
一行由空格隔開的兩個非負整數，分別是n和p。

輸出
一行表示答案。

樣例輸入
復制樣例數據
5 97
樣例輸出
11

提示
時間限制: 1 Sec 內存限制: 128 MB
提交: 108 解決: 15
[提交] [狀態] [命題人:admin]
題目描述
大鳳號航空母艦很喜歡算術。
它，是舊日本海軍中最為先進的航空母艦。
它，是舊日本海軍中最為短命的航空母艦。
同時，她還是最平的航空母艦（龍驤：你說啥？）
如此多第一 ……
一生二，二生三，三生萬物 ……
這也許就是大鳳喜歡算術的原因吧。
有一天，她看到了這樣一道題：
令
電探發現了來自遠處的魚雷，時間不多了。

輸入
一行由空格隔開的兩個非負整數，分別是n和p。

輸出
一行表示答案。

樣例輸入
復制樣例數據
5 97
樣例輸出
11

提示

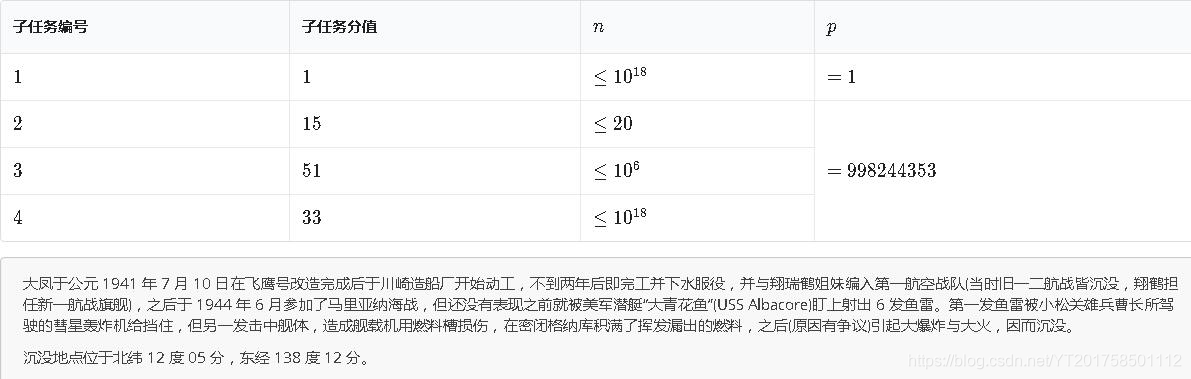
解題思路：
通過打表，得

可以推出對于$?x^n?$的值$dp[n]$滿足：
$dp[n]=f[n]+f[n?2]$即$dp[n]=f[n?1]+2?f[n?2]$
當$n$時：$dp[n]$
否則 ：$dp[n]?1$
因此可以通過矩陣快速冪來快速計算$dp[n]$,可得：
$\left|\begin{array}{ccc}dp[n]& f[n]& f[n?1]\\ 0& 0& 0\\ 0& 0& 0\end{array}\right|$ =$\left|\begin{array}{ccc}0& f[1]& f[0]\\ 0& 0& 0\\ 0& 0& 0\end{array}\right|$*${\left|\begin{array}{ccc}0& 0& 0\\ 1& 1& 1\\ 2& 1& 1\end{array}\right|}^n$
因此通過矩陣快速冪求得$dp[n]$的值，再根據$n$的奇偶分類討論即可。
ps:需特判一下$n$為0的情況
代碼：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <bitset>
#include <set>
#include <utility>
#include <sstream>
#include <iomanip>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define lep(i,l,r) for(int i=l;i>=r;i--)
#define ms(arr) memset(arr,0,sizeof(arr))
//priority_queue<int,vector<int> ,greater<int> >q;
const int maxn = (int)1e5 + 5;
const ll mod = 1e9+7;
struct node
{ll arr[3][3];node() {ms(arr);}
};
ll p;
node mul(node a,node b) {node c;for(int i=0;i<3;i++) {for(int j=0;j<3;j++) {for(int k=0;k<3;k++) {c.arr[i][j]=(c.arr[i][j]+(a.arr[i][k]*b.arr[k][j])%p)%p;}}}return c;
}
ll quickpow(ll n) {node a,b;a.arr[0][0]=a.arr[0][1]=a.arr[0][2]=a.arr[2][2]=0;a.arr[1][0]=a.arr[1][1]=a.arr[1][2]=a.arr[2][1]=1;a.arr[2][0]=2;b.arr[0][0]=b.arr[0][1]=1;b.arr[0][2]=b.arr[1][0]=b.arr[1][1]=b.arr[1][2]=0;b.arr[2][0]=b.arr[2][1]=b.arr[2][2]=0;while(n) {if(n&1) b=mul(b,a);a=mul(a,a);n>>=1;}return b.arr[0][0]%p;
}
int main() 
{#ifndef ONLINE_JUDGEfreopen("in.txt", "r", stdin);#endif//freopen("out.txt", "w", stdout);//ios::sync_with_stdio(0),cin.tie(0);ll n;scanf("%lld %lld",&n,&p);ll ans=quickpow(n);if(n==0) printf("%lld\n",1%p);else {if(n%2==1) printf("%lld\n",ans);else {printf("%lld\n",(ans-1+p)%p);}}return 0;
}