我們做個總結吧

數組理論基礎

數組是非常基礎的數據結構，在面試中，考察數組的題目一般在思維上都不難，主要是考察對代碼的掌控能力

也就是說，想法很簡單，但實現起來 可能就不是那么回事了。

首先要知道數組在內存中的存儲方式，這樣才能真正理解數組相關的面試題

「數組是存放在連續內存空間上的相同類型數據的集合。」

數組可以方便的通過下表索引的方式獲取到下表下對應的數據。

舉一個字符數組的例子，如圖所示：

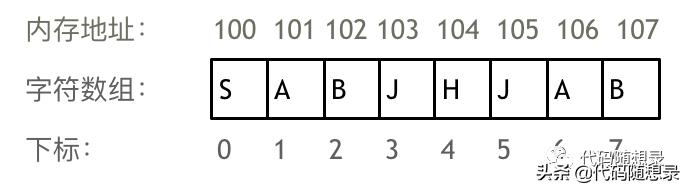
需要兩點注意的是

• 「數組下表都是從0開始的。」
• 「數組內存空間的地址是連續的」

正是「因為數組的在內存空間的地址是連續的，所以我們在刪除或者增添元素的時候，就難免要移動其他元素的地址。」

例如刪除下表為3的元素，需要對下表為3的元素后面的所有元素都要做移動操作，如圖所示：

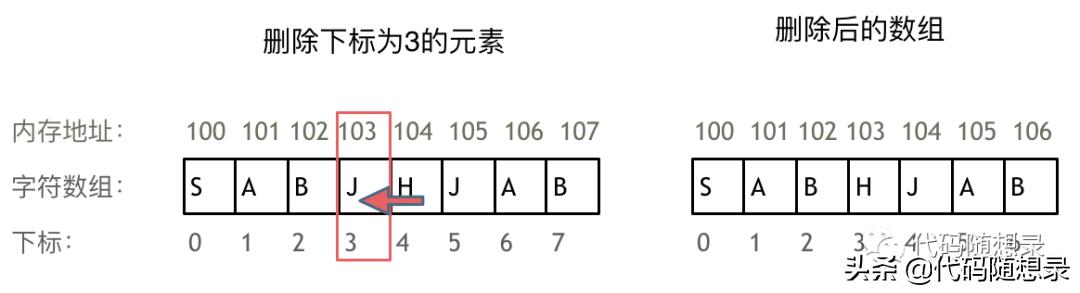
而且大家如果使用C++的話，要注意vector 和 array的區別，vector的底層實現是array，嚴格來講vector是容器，不是數組。

「數組的元素是不能刪的，只能覆蓋。」

那么二維數組直接上圖，大家應該就知道怎么回事了

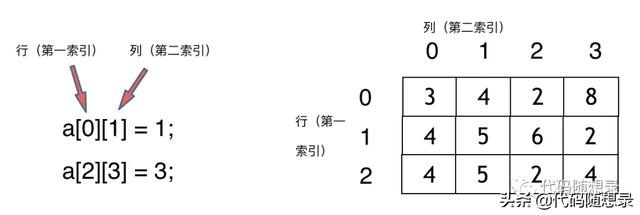
「那么二維數組在內存的空間地址是連續的么？」

我們來舉一個例子，例如：int[][] rating = new int[3][4]; ， 這個二維數據在內存空間可不是一個 3*4 的連續地址空間

看了下圖，就應該明白了：

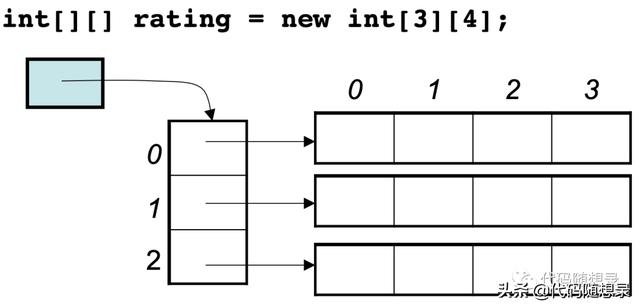
所以「二維數據在內存中不是 3*4 的連續地址空間，而是四條連續的地址空間組成！」

數組的經典題目

在面試中，數組是必考的基礎數據結構。

其實數據的題目在思想上一般比較簡單的，但是如果想高效，并不容易。

我們之前一共講解了四道經典數組題目，每一道題目都代表一個類型，一種思想。

二分法

數組：每次遇到二分法，都是一看就會，一寫就廢

這道題目呢，考察的數據的基本操作，思路很簡單，但是在通過率在簡單題里并不高，不要輕敵。

可以使用暴力解法，通過這道題目，如果要求更優的算法，建議試一試用二分法，來解決這道題目

暴力解法時間復雜度：O(n)
二分法時間復雜度：O(logn)

在這道題目中我們講到了「循環不變量原則」，只有在循環中堅持對區間的定義，才能清楚的把握循環中的各種細節。

「二分法是算法面試中的常考題，建議通過這道題目，鍛煉自己手撕二分的能力」。

雙指針法

數組：就移除個元素很難么？

雙指針法(快慢指針法)：「通過一個快指針和慢指針在一個for循環下完成兩個for循環的工作。」

暴力解法時間復雜度：O(n^2)
雙指針時間復雜度：O(n)

這道題目迷惑了不少同學，糾結于數組中的元素為什么不能刪除，主要是因為以下兩點：

• 數組在內存中是連續的地址空間，不能釋放單一元素，如果要釋放，就是全釋放(程序運行結束，回收內存棧空間)。
• C++中vector和array的區別一定要弄清楚，vector的底層實現是array，所以vector展現出友好的一些都是因為經過包裝了。

雙指針法(快慢指針法)在數組和鏈表的操作中是非常常見的，很多考察數組和鏈表操作的面試題，都使用雙指針法。

滑動窗口

數組：滑動窗口拯救了你

本題介紹了數組操作中的另一個重要思想：滑動窗口。

暴力解法時間復雜度：O(n^2)
滑動窗口時間復雜度：O(n)

本題中，主要要理解滑動窗口如何移動 窗口起始位置，達到動態更新窗口大小的，從而得出長度最小的符合條件的長度。

「滑動窗口的精妙之處在于根據當前子序列和大小的情況，不斷調節子序列的起始位置。從而將O(n^2)的暴力解法降為O(n)。」

如果沒有接觸過這一類的方法，很難想到類似的解題思路，滑動窗口方法還是很巧妙的。

模擬行為

數組：這個循環可以轉懵很多人

模擬類的題目在數組中很常見，不涉及到什么算法，就是單純的模擬，十分考察大家對代碼的掌控能力。

在這道題目中，我們再一次介紹到了「循環不變量原則」，其實這也是寫程序中的重要原則。

相信大家又遇到過這種情況：感覺題目的邊界調節超多，一波接著一波的判斷，找邊界，踩了東墻補西墻，好不容易運行通過了，代碼寫的十分冗余，毫無章法，其實「真正解決題目的代碼都是簡潔的，或者有原則性的」，大家可以在這道題目中體會到這一點。

總結

從二分法到雙指針，從滑動窗口到螺旋矩陣，相信如果大家真的認真做了「代碼隨想錄」每日推薦的題目，定會有所收獲。

推薦的題目即使大家之前做過了，再讀一遍的文章，也會幫助你提煉出解題的精髓所在。

「如果感覺有所收獲，希望大家多多支持，打卡轉發，點贊在看 都是對我最大的鼓勵！」

最后，大家周末愉快！

在留言區留下你的思路吧！

-------end-------

我將算法學習相關的資料已經整理到了Github ：https://github.com/youngyangyang04/leetcode-master，里面還有leetcode刷題攻略、各個類型經典題目刷題順序、思維導圖看一看一定會有所收獲！

每天8:35準時推送一道經典算法題目，推送的每道題目都不是孤立的，而是由淺入深，環環相扣，幫你梳理算法知識脈絡，輕松學算法！

「@代碼隨想錄」期待你的關注！