相信大家在小學奧數中都遇到這樣一個問題：4條直線最多能將平面分成幾部分？這個問題并不能難倒我們，但是如果將問題改為：4個平面最多能將空間分為幾部分？這下子我們可能就要放棄了。

為了解決這個問題，今天我們就來研究一組相關的問題，這些問題的解決方案都涉及數學歸納法。

問題1 :?個點最多能將一條直線分為多少個區域?

1個點：

2個點：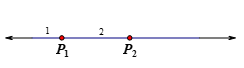

3個點：

點數	1	2	3	...	個點
區域數	2	3	4	...

從表中我們容易猜想得出，個點最多能將一條直線分為個區域。為了表述方便，令

直線上個點所決定的直線上區域的最大個數

當一個額外的點被添加到這條直線上會發生什么呢？

我們觀察一下：每次一個新的點被添加到這條直線上，它必須被插入到由之前的點決定的一個現有的區域中。因此，該區域被劃分為兩個區域和，而之前的所有其他區域保持不變。因此，當向直線添加一個新點時，只添加一個新區域。

因此我們得到一個循環關系：

這樣，我們可以推導出顯性公式：

接下來我們使用數學歸納法進行證明。

設命題:

• 基步：，因此真。
• 歸納步：假設真，即對成立。通過遞推關系有?也成立。

因此根據數學歸納法，對所有成立。

問題2 :?條直線最多能將一個平面分為多少個區域?

1條直線：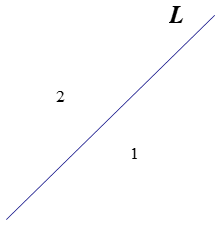

2條直線：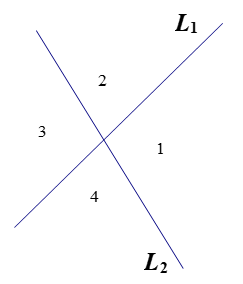

3條直線：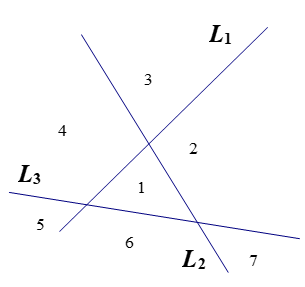

4條直線：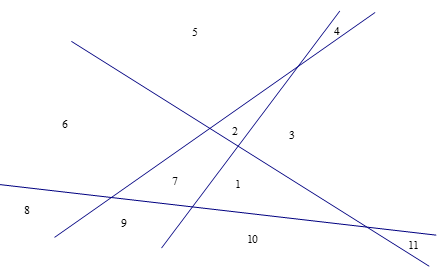

類似地，令

平面上條直線所決定的平面上區域的最大個數我們已經觀察到，如果是平面上條直線所確定的平面上的最大區域數，則，，，。

直線數 n	1	2	3	4	5	6	7
區域數	2	4	7	11

我們可以用同樣的方法求出，等等，但是這些圖越來越難構造。因此我們需要找到這個序列的顯性公式。我們可以采用有限差分法來構造這個序列的顯性公式，注意到第二排差值是1，2，3，4，第一排差值是1，1，1。因為第一排差值是常數，我們期望可能是的二次函數。令

其中、、為常數，可由上表中的部分數據確定。然后，使用表中的值(列一個三元一次方程組)，解得因此，對于的顯性公式的一個猜想是我們來看看如果5條直線的情況。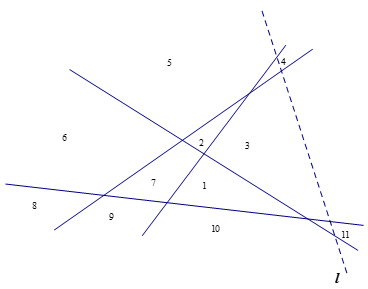

因為不平行于任何其他直線，也不經過其他直線任何較早的交點，所以每次與現有直線相交時，它就把它所經過的區域分成兩個區域。當經過第四條直線后，又將最后一個區域劃分為兩個區域。簡言之，第5條直線產生了5個新區域。同樣的論證表明，將第條線添加到n條線的組合中會產生個新區域。我們可以把它表示為一個遞歸關系：

同樣地，我們可以用數學歸納法證明顯性公式成立，這里不再贅述。

問題3 : 空間中個平面最多劃分多少個區域?

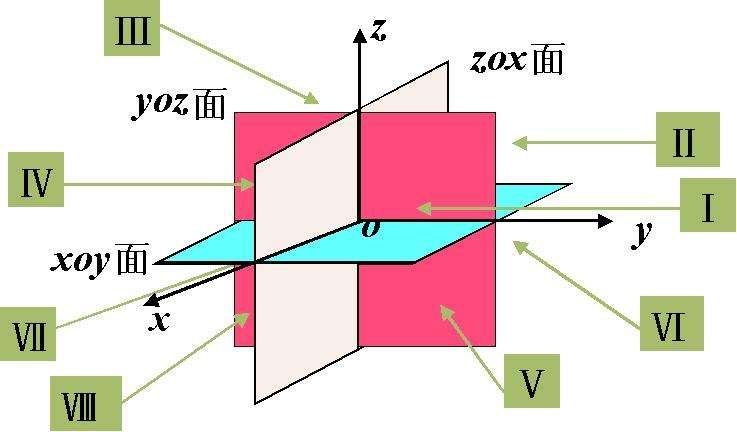
令

空間中個平面所決定的最大區域數觀察上圖可得，，。但是你可能會發現用圖來表示的情況很困難，因為圖很復雜。

想象一下在三個平面的圖形中添加第四個平面的結果。給定三個平面都會與新平面有一條交線，三條直線最多能將平面分為7個區域。因此，再使用有限差分法(列一個四元一次方程組)來構造序列的顯性公式:

現在嘗試聯系問題1、2、3

我們看下表：

元素個數	分割直線數	分割平面數	分割空間數
0	1	1	1
1	2	2	2
2	3	4	4
3	4	7	8
4	5	11	15
...	...	...	...
條直線	個

注意到，在表格中

對所有自然數成立。

這樣我們就解決了最開始提出的問題。

參考文獻[1]G.波利亞.數學與猜想:數學中的歸納和類比(第1卷)[M].科學出版社，2001.

【往期回顧】

• 圖解數學

圖解裝錯信封問題

人人都能看懂的美妙證明！圖解柏拉圖多面體和歐拉公式

在紙上投針就能算出圓周率π？圖解蒲豐投針實驗

什么是數列的極限？圖解ε-N語言

• 數學文化：

原來數學還可以這樣！

• 生活中的數學：

找東西背后的概率問題

一局俄羅斯方塊可以一直玩下去嗎？

• 公式之美：

你還在死記自然數平方和的公式嗎？那你就not fashion了！

最短的證明有多短！？

最短的證明有多短！？(二)

喜歡就點亮在看，謝謝支持