點擊上方藍色字體,關注AI小白入門喲

作者 | 文杰
編輯 | yuquanle
本文介紹線性回歸模型,從梯度下降和最小二乘的角度來求解線性回歸問題,以概率的方式解釋了線性回歸為什么采用平方損失,然后介紹了線性回歸中常用的兩種范數來解決過擬合和矩陣不可逆的情況,分別對應嶺回歸和Lasso回歸,最后考慮到線性回歸的局限性,介紹了一種局部加權線性回歸,增加其非線性表示能力
線性回歸
A、線性回歸
假設有數據有:
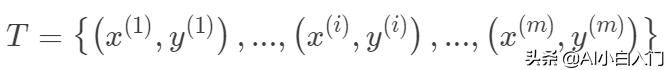
其中
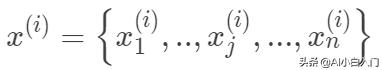
,
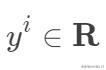
。其中m為訓練集樣本數,n為樣本維度,y是樣本的真實值。線性回歸采用一個高維的線性函數來盡可能的擬合所有的數據點,最簡單的想法就是最小化函數值與真實值誤差的平方(概率解釋-高斯分布加最大似然估計)。即有如下目標函數:
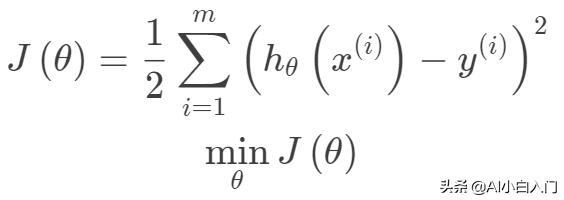
其中線性函數如下:
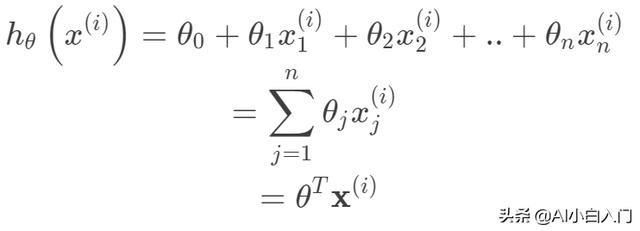
構建好線性回歸模型的目標函數之后,接下來就是求解目標函數的最優解,即一個優化問題。常用的梯度優化方法都可以拿來用,這里以梯度下降法來求解目標函數。
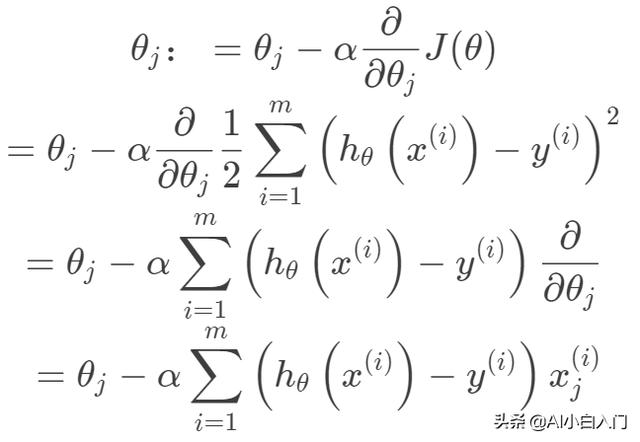
另外,線性回歸也可以從最小二乘法的角度來看,下面先將樣本表示向量化,
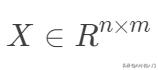
,
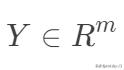
,構成如下數據矩陣。
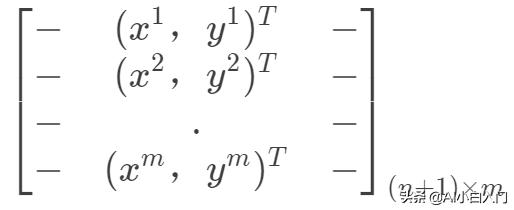
那么目標函數向量化形式如下:
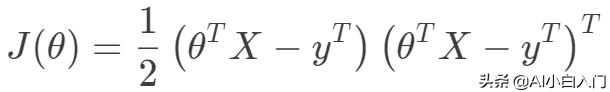
可以看出目標函數是一個凸二次規劃問題,其最優解在導數為0處取到。
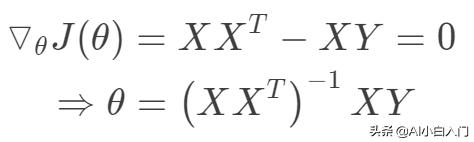
值得注意的上式中存在計算矩陣的逆,一般來講當樣本數大于數據維度時,矩陣可逆,可以采用最小二乘法求得目標函數的閉式解。當數據維度大于樣本數時,矩陣線性相關,不可逆。此時最小化目標函數解不唯一,且非常多,出于這樣一種情況,我們可以考慮奧卡姆剃刀準則來簡化模型復雜度,使其不必要的特征對應的w為0。所以引入正則項使得模型中w非0個數最少。當然,嶺回歸,lasso回歸的最根本的目的不是解決不可逆問題,而是防止過擬合。
B、概率解釋
損失函數與最小二乘法采用最小化平方和的概率解釋。假設模型預測值與真實值的誤差為
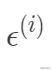
,那么預測值
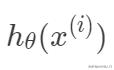
與真實值
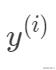
之間有如下關系:
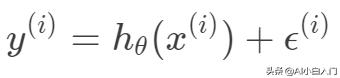
根據中心極限定理,當一個事件與很多獨立隨機變量有關,該事件服從正態分布 。一般來說,連續值我們都傾向于假設服從正態分布。假設每個樣本的誤差
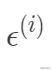
獨立同分布均值為0,方差為σ的高斯分布
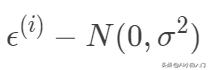
,所以有:
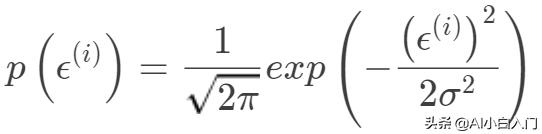
即表示
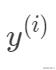
滿足以均值為
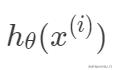
,方差為
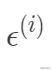
的高斯分布。
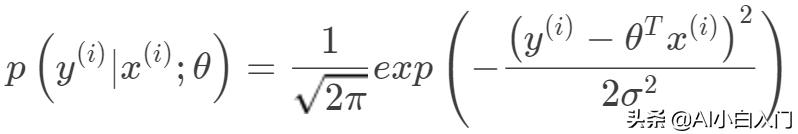
由最大似然估計有:
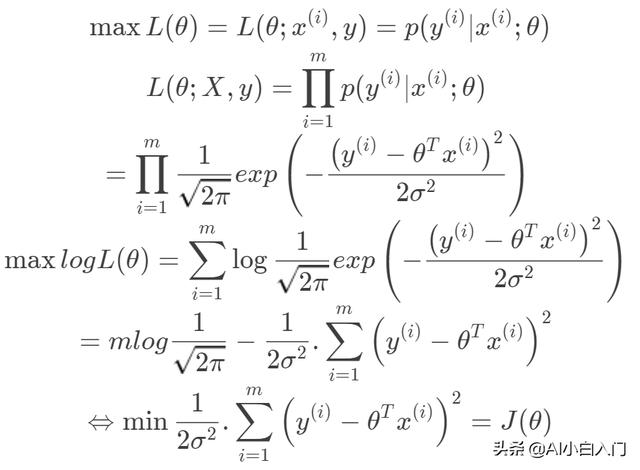
嶺回歸和Lasso回歸
嶺回歸的目標函數在一般的線性回歸的基礎上加入了正則項,在保證最佳擬合誤差的同時,使得參數盡可能的“簡單”,使得模型的泛化能力強(即不過分相信從訓練數據中學到的知識)。正則項一般采用一,二范數,使得模型更具有泛化性,同時可以解決線性回歸中不可逆情況。
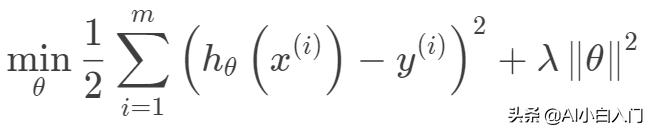
其迭代優化函數如下:
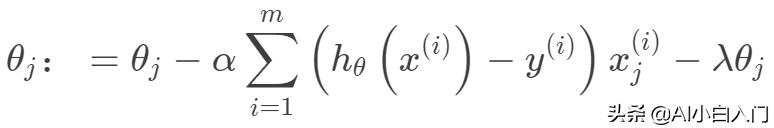
另外從最小二乘的角度來看,通過引入二范正則項,使其主對角線元素來強制矩陣可逆。
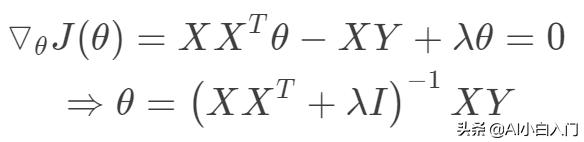
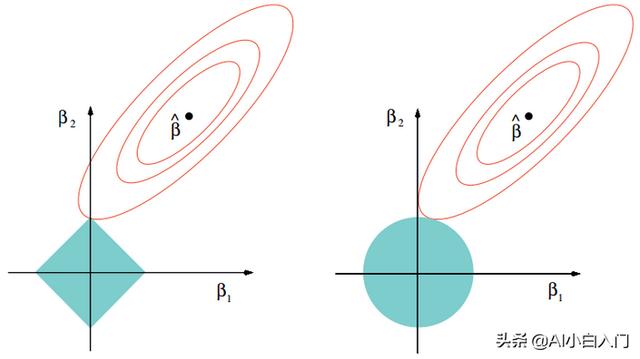
Lasso回歸采用一范數來約束,使參數非零個數最少。而Lasso和嶺回歸的區別很好理解,在優化過程中,最優解為函數等值線與約束空間的交集,正則項可以看作是約束空間。可以看出二范的約束空間是一個球形,而一范的約束空間是一個方形,這也就是二范會得到很多參數接近0的值,而一范則盡可能非零參數最少。
值得注意的是線性模型的表示能力有限,但是并不一定表示線性模型只能處理線性分布的數據。這里有兩種常用的線性模型非線性化。對于上面的線性函數的構造,我們可以看出模型在以
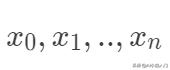
的坐標上是線性的,但是并不表示線性的模型就一定只能用于線性分布問題上。假如我們只有一個特征
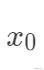
,而實際上回歸值是
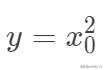
等,我們同樣可以采用線性模型,因為我們完全可以把輸入空間映射到高維空間
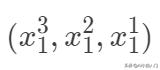
,其實這也是核方法以及PCA空間變換的一種思想,凡是對輸入空間進行線性,非線性的變換,都是把輸入空間映射到特征空間的思想,所以只需要把非線性問題轉化為線性問題即可。另外一種是局部線性思想,即對每一個樣本構建一個加權的線性模型。
局部加權線性回歸
考慮到線性回歸的表示能力有限,可能出現欠擬合現象。局部加權線性回歸為每一個待預測的點構建一個加權的線性模型。其加權的方式是根據預測點與數據集中點的距離來為數據集中的點賦權重,當某點距離預測點較遠時,其權重較小,反之較大。由于這種權重的機制引入使得局部加權線性回歸產生了一種局部分段擬合的效果。由于該方法對于每一個預測點構建一個加權線性模型,都要重新計算與數據集中所有點的距離來確定權重值,進而確定針對該預測點的線性模型,計算成本高,同時為了實現無參估計來計算權重,需要存儲整個數據集。
局部加權線性回歸,在線性回歸基礎上引入權重,其目標函數(下面的目標函數是針對一個預測樣本的)如下:
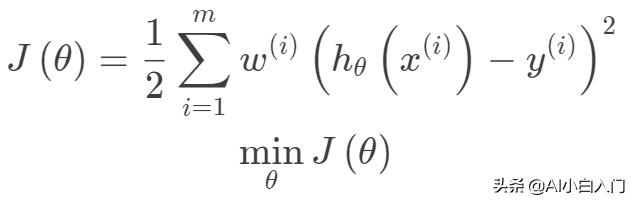
一般選擇下面的權重函數,權重函數選擇并非因為其類似于高斯函數,而是根據數據分布的特性,但權重函數的選取并不一定依賴于數據特性。
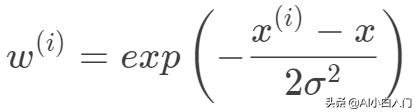
其中是待預測的一個數據點。
對于上面的目標函數,我們的目標同樣是求解使得損失函數最小化,同樣局部加權線性回歸可以采用梯度的方法,也可以從最小二乘法的角度給出閉式解。
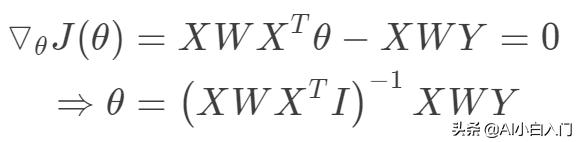
其中
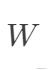
是對角矩陣,
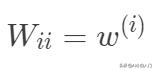
。
線性回歸核心思想最小化平方誤差,可以從最小化損失函數和最小二乘角度來看,優化過程可以采用梯度方法和閉式解。在閉式解問題中需要注意矩陣可逆問題。考慮到過擬合和欠擬合問題,有嶺回歸和lasso回歸來防止過擬合,局部加權線性回歸通過加權實現非線性表示。
代碼實戰
A、線性回歸
/**線性回歸函數的實現,考慮一般的線性回歸,最小平方和作為損失函數,則目標函數是一個無約束的凸二次規劃問題,由凸二次規劃問題的極小值在導數為0處取到,且極小值為全局最小值,且有閉式解。根據數學表達式實現矩陣之間的運算求得參數w。**/int regression(Matrix x,Matrix y){ Matrix xT=x.transposeMatrix(); Matrix xTx=xTx.multsMatrix(xT,x); Matrix xTx_1=xTx.niMatrix(); Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT); Matrix ws; ws=ws.multsMatrix(xTx_1xT,y); cout<B、嶺回歸和Lasso回歸
/**下面的嶺回歸函數只是在一般的線性回歸函數的基礎上在對角線上引入了嶺的概念,不僅有解決矩陣不可逆的線性,同樣也有正則項的目的,采用常用的二范數就得到了直接引入lam的形式。**/int ridgeRegres(Matrix x,Matrix y,double lam){ Matrix xT=x.transposeMatrix(); Matrix xTx=xTx.multsMatrix(xT,x); Matrix denom(xTx.row,xTx.col,lam,"diag"); xTx=xTx.addMatrix(xTx,denom); Matrix xTx_1=xTx.niMatrix(); Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT); Matrix ws=ws.multsMatrix(xTx_1xT,y); cout<C、局部加權線性回歸
/**局部加權線性回歸是在線性回歸的基礎上對每一個測試樣本(訓練的時候就是每一個訓練樣本)在其已有的樣本進行一個加權擬合,權重的確定可以通過一個核來計算,常用的有高斯核(離測試樣本越近,權重越大,反之越小),這樣對每一個測試樣本就得到了不一樣的權重向量,所以最后得出的擬合曲線不再是線性的了,這樣就增加的模型的復雜度來更好的擬合非線性數據。**///需要注意的是局部加權線性回歸是對每一個樣本進行權重計算,所以對于每一個樣本都有一個權重w,所以下面的函數只是局部線性回歸的一個主要輔助函數Matrix locWeightLineReg(Matrix test,Matrix x,Matrix y,const double &k){ Matrix w(x.row,x.row,0,"T"); double temp=0; int i,j; /** 根據測試樣本點與整個樣本的距離已經選擇的核確定局部加權矩陣,采用對角線上為局部加權值 **/ for(i=0;i詳細代碼: https://github.com/myazi/myLearn/blob/master/LineReg.cpp
The End







)








)


