常見的線性模型：

求解方式有兩種，一種是計算均方誤差（MSE），使得均方誤差最小。

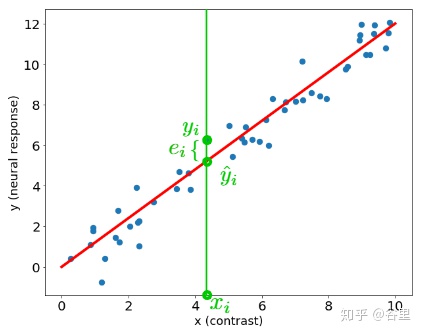
找到梯度為零的點即可。

而之前一直比較模糊的最大似然法也比較清楚了。一般線性模型，我們假定誤差項是符合高斯分布的，高斯分布的概率密度函數為：

這里x即為原始值，

為估計值，原始描述的是原始點在均值周圍的分布，現在改成估計值圍繞原始值的分布即可。以下便是線性模型的似然函數

我們要找的就是使得p值最大的theta。取log是為了求值的方便，下面的推導直接把前面部分分離出來了，因為是個常數，可以直接不看，看后半部分就行了。

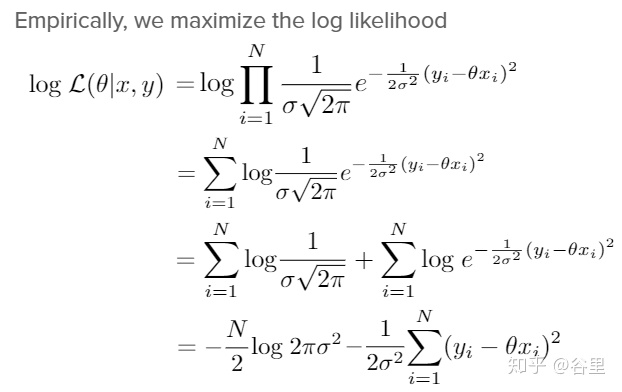
這樣，我們看只要求后半部分的極值就行了，由于是負號，求其最大值就是求不帶負號的最小值，這樣就跟MSE的公式幾乎一樣了。

從概念上講就是，由于誤差項是高斯分布的，而估計值是一個確定值，所以當前真實值其實是落在以估計值為中心的高斯分布上的，如下

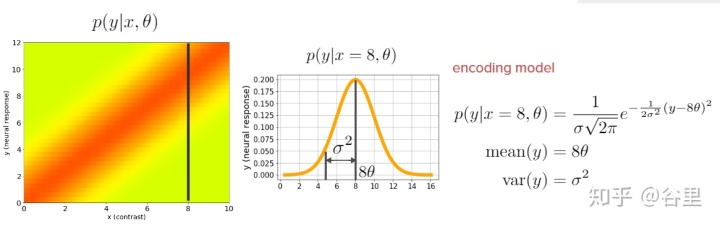
我們想要估計值盡可能等于真實值，那么使真實值最好就落在高斯分布的最高點上，即概率最大點，所以我們把每個真實值的落在各自估計值的高斯分布的概率加起來最大，就可以說是最佳的擬合程度了。由于加了log，所以累加在圖2中變成了累乘。

而這個極大似然估計也概念化地解釋了過擬合欠擬合中地bias-variance問題，variance就是指這個分布地寬窄，如果過寬，variance過大，即我們的模型變異很大，可能加一個或減一個數據，參數都會變很多。

而估算variance可以用bootstrap來做，bootstrap的過程就是，加入我們有10各樣本，就取隨機在10個樣本中抽取10個樣本，但是抽取方式是可以重復的，因此我們又得到了10個樣本，只是可能有重復樣本。

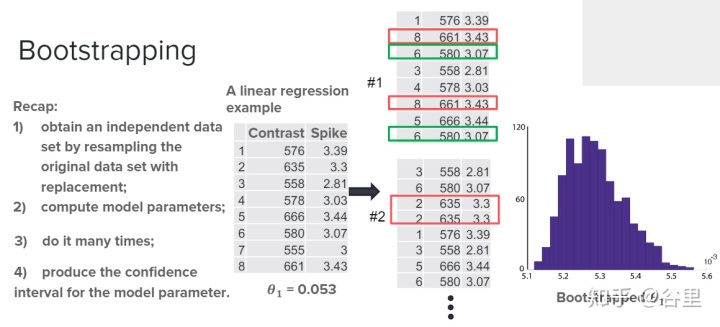
看一下代碼就很清楚了。

def resample_with_replacement(x, y):"""Resample data points with replacement from the dataset of `x` inputs and`y` measurements.Args:x (ndarray): An array of shape (samples,) that contains the input values.y (ndarray): An array of shape (samples,) that contains the correspondingmeasurement values to the inputs.Returns:ndarray, ndarray: The newly resampled `x` and `y` data points."""# Get array of indices for resampled pointssample_idx = np.random.choice(len(x), size=len(x), replace=True)# Sample from x and y according to sample_idxx_ = x[sample_idx]y_ = y[sample_idx]return x_, y_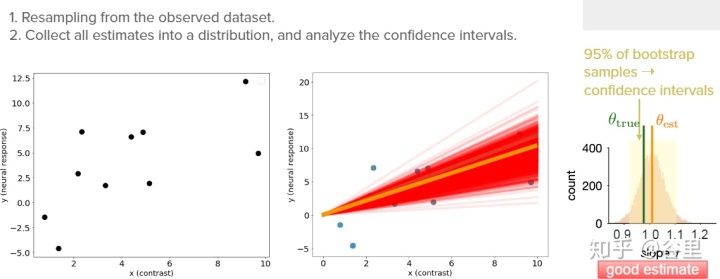

這樣就可以通過bootstrap來估計出我們參數的置信區間，雖然我們無從知道真實值是什么樣的，但是給一個區間總比一個點信息更多一點。當然有的顯著性檢驗應該可以用這個區間有沒有過0點來做。

除了bootstrapping可以給出模型的variance，還可以使用交叉驗證的方法評估模型，把所有數據分成n塊，每次用其中一塊做驗證集，其他為測試集。是測試集的平均正確率來判斷模型表現。這里要注意，一般都會做標準化，不能在劃分驗證集和測試集之前做，這樣會帶來很多的假陽性。一個辦法是對訓練集標準化，然把用得到的標準化參數應用到測試集上。

以上，我們的假設是誤差項為高斯分布，而不是所有都符合高斯分布的，如，如果反應是多個離散值的分布，那么我們的誤差項分布使用泊松分布更好。這樣就是個非線性的模型了，做起來很簡單，只需要在線性模型中間加一步非線性轉化，將原來的線性模型得到的輸出，套一個非線性方程即可，這也就是所謂的廣義線性模型（GLM）。

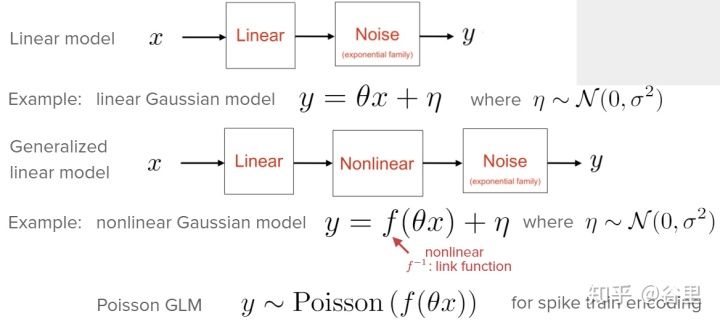
而二值分布只需要將非線性方程設置為sigmoid方程，套上即可，這就是Logistic回歸。

這樣就是可以用glm，只是在原來的線性模型加一步非線性轉化就可以結果多樣的問題。

使用正則化解決過擬合問題，詳見：

上圖均來自于NMA2020的tutorial，代碼來自示例代碼：