[2021-CVPR] Fine-grained Angular Contrastive Learning with Coarse Labels 論文簡析

論文地址：https://arxiv.org/abs/2012.03515

代碼地址：https://github.com/guybuk/ANCOR

首先通俗地介紹一下細粒度（fine-grained），細粒度分類是指在原來粗分類的基礎上再對子類進行更細致的分類。舉個例子，圖中有一只狗，粗（coarse）分類的分類結果即是一只狗，而細粒度的分類結果則會細致到這只狗是什么品種，是比格，柯利還是哈巴狗。

本文提出了一個新任務C2FS（Coarse-to-Fine Few-Shot），即由粗粒度轉向細粒度的小樣本的分類任務，在訓練階段使用粗類樣本進行訓練，在測試階段經過細粒度子類小樣本數據集的微調之后測試細粒度子類的分類準確度。

并提出了一個針對該任務的網絡架構，使用有監督學習對樣本進行粗分類，使用自監督對比學習（文中用的是MoCo V2）進行細粒度分類，并針對兩種分類訓練時損失函數會沖突的問題提出了Angular Normalization模塊，將自監督的infoNCE損失轉移到角度空間，從而提升兩個分類任務之間損失函數的協同性。

整體網絡結構如下：

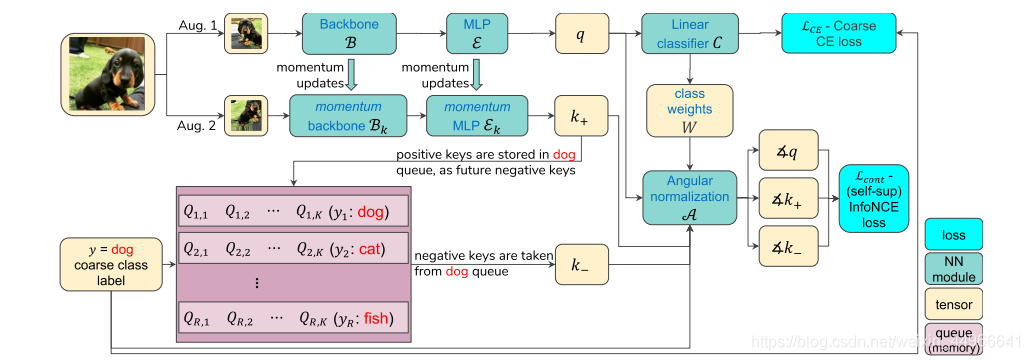
其中針對粗分類的任務，根據粗類標簽進行有監督學習，來將粗類之間分開，損失函數就是我們熟悉的交叉熵。而針對粗類的子類進行細粒度分類時，作者使用了最近大火的自監督對比學習，具體使用的是何愷明團隊的MoCo V2，使得屬于同一個粗類內的每個不同的實例分開有一定距離，損失函數是最近對比學習最常用的infoNCE，但針對兩損失的沖突問題，對infoNCE的輸入進行了一些改動。

具體流程是：一張圖片（實際上訓練是在batch內進行的，這點對于對比學習來說很關鍵，上圖簡明起見用一張圖片表示）輸入進來以后，經過兩種不同的數據擴增方法（Aug. 1,2）得到同一張原圖的兩張圖片 $x_q$ ， $x_k$，然后其中 $x_q$ 經過backbone $\mathcal{B}$ （就是MoCo中的encoder_q）和MLP $\mathcal{E}$ 得到 $x_q$ 的特征表示 $q$ ，這個 $q$ 會經過一個分類器（全連接+Softmax）得到粗類的預測概率，而粗類分類的訓練是有標簽的，可以直接做交叉熵損失，這一部分是有監督的粗類分類訓練。

再說兩種數據擴增得到另一張圖片 $x_k$ ，它會經過動量更新的（詳見MoCo）${\mathcal{B}}_k$ 和 ${\mathcal{E}}_k$ ，得到特征表示 $k_{+}$ ，$k_{+}$ 會在對比學習中與 $q$ 組成正對（positive pair），而從MoCo維護的隊列中拿到的與輸入圖片屬于同一粗類（比如圖中的狗類）的不同圖片樣本 $k_{?}$ 會和 $q$ 組成負對（negative pair），從而根據 $q$ ，$k_{+}$ ，$k_{?}$ 計算infoNCE損失進行對比學習，來使得同一粗類內的不同樣本也有一定的距離，方便后面測試時進行小樣本的細粒度分類學習。

至此看起來一切順其自然，十分合理。但是作者敏銳地發現了一個重要問題：如下圖上半部分所示，粗類分類的有監督CE損失會使得同一粗類的每個樣本都盡量靠到一起，而對比學習infoNCE損失又會使得粗類中的每個樣本有一定的距離，也就是說這兩個損失會有沖突存在。

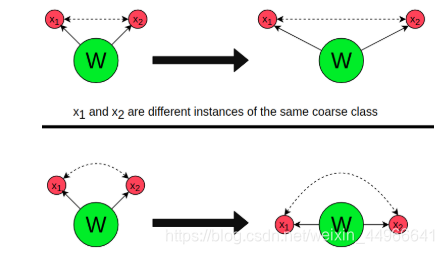
針對這個問題，作者提出了Angular Normalization（AN）模塊，來增強兩個損失之間的協同性（synergy）。

首先說明一些符號：輸入圖片 $I$ ，它的特征表示 $q$ ，它所屬的粗類 $y$ ，分類器 $C$ 的參數 $W$ 的第 $y$ 行 $W_y$ ，分類器 $C$ 中 $y$ 類的logit $W_{y}q$ 。

這樣，要想使CE損失 ${\mathcal{L}}_{CE}=(C(q),y)$ 最小，要 $W_{y}q$ 最大且 $W_{i=y}q$ 最小，也就是 $q$ (單位向量，embedder $\mathcal{E}$ 的最后再經過L2 norm)轉到 $W_y$ 的方向，這對所有的 $y$ 類的圖片都是相同的，會使他們倒向（collapse to）最接近 $W_y$ 的單位向量$\frac{W_y}{||W_y||}$ 。但是這種倒向（collapse）與 y 類特定的 InfoNCE 對比損失 ${\mathcal{L}}_{c}ont(q,k_{?},k_{+})$ 存在沖突，后者試圖將 $y$ 類的樣本彼此之間推開。

作者提出的解決方法即是AN，定義 $y$ 類的angular normalzation：
$$\mathcal{A}(x,W,y)=\angle x=\frac{\frac{x}{||x||}?\frac{W_y}{||W_y||}}{||\frac{x}{||x||}?\frac{W_y}{||W_y||}||}$$
這就將單位向量 $\frac{x}{||x||}$ 轉換為了表示其與 $\frac{W_y}{||W_y||}$ 的角度的單位向量。

根據以上定義，我們將 ${\mathcal{L}}_{cont}$ 中的 $q,k_{?},k_{+}$ 分別替換為它們的 $y$ 類angular normalization的形式：
$$\angle q=\mathcal{A}(q,W,y)$$
$$\angle k_{?}=\mathcal{A}(k_{?},W,y)$$
$$\angle k_{+}=\mathcal{A}(k_{+},W,y)$$

從而我們損失函數的最終形式就是：
$$\mathcal{L}={\mathcal{L}}_{CE}(C(y),y)+{\mathcal{L}}_{cont}(\angle q,\angle k_{+},\angle k_{?})$$
如上圖下方所示，改進后的AN形式的 ${\mathcal{L}}_{cont}$ 運作在角度空間中圍繞著 $\frac{W_y}{||W_y||}$ 的“軌道"（orbit）上。這樣就不會干擾到 ${\mathcal{L}}_{CE}$ 損失使倒向（collapse）$\frac{W_y}{||W_y||}$，即不會與CE損失產生沖突，從而提升了兩損失的協同性。

AN一個額外的好處是它忽視了（在normalize之后）到權重向量的距離，這樣可以保護 ${\mathcal{L}}_{cont}$ 不會收到不同子類間“松緊”程度的影響。

實驗部分有興趣可以去查看原文。

作為2021 CVPR的 oral，本文的質量還是很足的，一個頗有意思的新任務C2FS，并結合了一些最新的方法提出了一個比較合理的解決方案，還針對這個框架存在的一個關鍵問題有一個不錯的解決方案。

有理解不對的地方歡迎指正。