[2021-CVPR] Jigsaw Clustering for Unsupervised Visual Representation Learning 論文簡析及關鍵代碼簡析

論文：https://arxiv.org/abs/2104.00323

代碼：https://github.com/dvlab-research/JigsawClustering

總結

本文提出了一種單批次（single-batch）的自監督任務pretext task Jigsaw Cluster，相比于雙批次（dual-batches）的方法降低了計算量，同時利用了圖像內的信息和圖像間的信息。

本文提出的任務構造的主要流程如下如圖1所示，首先在一整個batch內將 $n$ 張圖像每張分為 $m\times m$ 份圖塊，則共有 $n\times m\times m$ 個圖塊。再將這些圖塊打亂（注意是一個batch內所有的圖塊進行打亂，而非某單張圖像內打亂）后，再拼接為圖像。

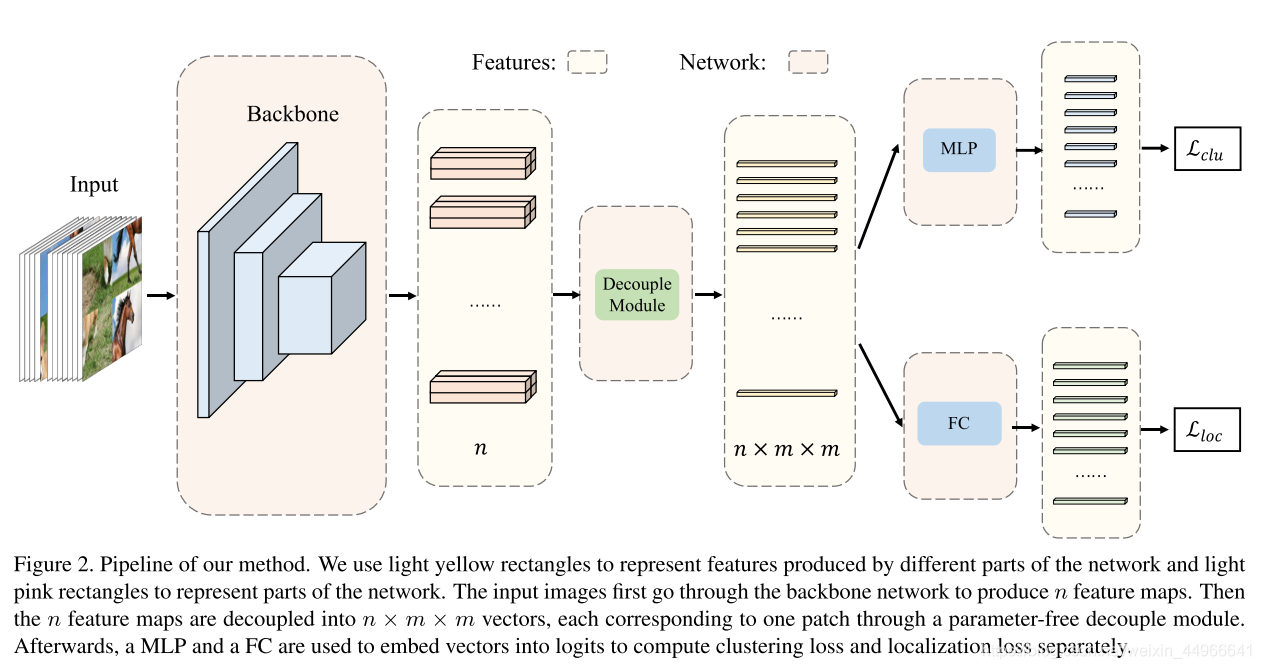
本文設計的網絡（如圖2所示）在backbone提取特征之后有兩個分支：聚類分支和定位分支。聚類分支會完成一個有監督聚類的任務，將來自同一張原圖的不同圖塊（已被打亂）聚集到一簇（cluster，類）。作者使用了最近比較火的對比學習來完成這個有監督聚類任務。而對于定位分支，則是要預測出圖塊在原圖中的位置，具體是由一個分類任務來完成，損失函數直接選用交叉熵損失。

算法細節如有重疊分塊、插值加池化等可見下面的原文翻譯。

源碼簡析

以下是源碼中JigClu模型的關鍵幾步操作，筆者在進行實驗后將其中信號流的形狀等信息注釋在代碼中，希望能夠幫助大家理解，或者能夠為想要復現并改進本文的讀者提供一些參考。

    @torch.no_grad()def _batch_gather_ddp(self, images):        # images是長度為4的列表，其中每個元素是形狀為 (n, 3, 112, 112)的tensor"""gather images from different gpus and shuffle between them*** Only support DistributedDataParallel (DDP) model. ***"""images_gather = []for i in range(4):batch_size_this = images[i].shape[0]images_gather.append(concat_all_gather(images[i]))batch_size_all = images_gather[i].shape[0]num_gpus = batch_size_all // batch_size_thisn,c,h,w = images_gather[0].shapepermute = torch.randperm(n*4).cuda()torch.distributed.broadcast(permute, src=0)images_gather = torch.cat(images_gather, dim=0)images_gather = images_gather[permute,:,:,:]col1 = torch.cat([images_gather[0:n], images_gather[n:2*n]], dim=3)col2 = torch.cat([images_gather[2*n:3*n], images_gather[3*n:]], dim=3)images_gather = torch.cat([col1, col2], dim=2)bs = images_gather.shape[0] // num_gpusgpu_idx = torch.distributed.get_rank()return images_gather[bs*gpu_idx:bs*(gpu_idx+1)], permute, ndef forward(self, images, progress):images_gather, permute, bs_all = self._batch_gather_ddp(images)     # bs=16雙卡,  len(images) 4, images_gather.shape  (8, 3, 224, 224), permute.shape 64(即16*4), bs_all = 16# compute featuresq = self.encoder(images_gather)         #  bs=16雙卡, q.shape  (8, 2048, 2, 2) q_gather = concat_all_gather(q)         #  bs=16雙卡, q_gather.shape   (16, 2048, 2, 2)     # 插值后池化，得到這個形狀n,c,h,w = q_gather.shapec1,c2 = q_gather.split([1,1],dim=2)         # bs=16雙卡, c.shape (16, 2048, 1, 2)f1,f2 = c1.split([1,1],dim=3)               # bs=16雙卡, f.shape (16, 2048, 1, 1)f3,f4 = c2.split([1,1],dim=3)q_gather = torch.cat([f1,f2,f3,f4],dim=0)   # bs=16雙卡, q_gather.shape (64, 2048, 1, 1)q_gather = q_gather.view(n*4,-1)            # bs=16雙卡, q_gather.shape (64, 2048)# clustering branchlabel_clu = permute % bs_all            # permute: 0-(4*bs) 之間的隨機值， 取余則label_clu: 4組 0-bs之間的隨機值，即同一個值label_clu值是來自同一圖片的q_clu = self.encoder.fc_clu(q_gather)       # bs=16雙卡，q_clu.shape (64, 128) 即(4*bs, dim)q_clu = nn.functional.normalize(q_clu, dim=1)loss_clu = self.criterion_clu(q_clu, label_clu)# location branchlabel_loc = torch.LongTensor([0]*bs_all+[1]*bs_all+[2]*bs_all+[3]*bs_all).cuda()label_loc = label_loc[permute]q_loc = self.encoder.fc_loc(q_gather)loss_loc = self.criterion_loc(q_loc, label_loc)return loss_clu, loss_loc

筆者使用雙卡進行實驗，batchsize設為16。

源碼中一些gather操作是為了適應dp或者ddp訓練，對理解算法本身沒有影響。

以下是筆者對原文部分進行的翻譯，一些算法細節和實現細節可以從中找到，配合源碼注釋基本可以理解全文的算法思想。有疑惑或者異議歡迎留言討論。

原文部分翻譯

abstract

使用對比學習的無監督表示學習取得了巨大的成功，該方法將每一訓練批次復制來構建對比對，使每一訓練批及其擴增版本同時進行前向傳播，導致額外計算。本文提出了一種新的jigsaw聚類 pretext task，該任務只需要將每個訓練批次本身進行前向傳播，并降低訓練損失。我們的方法同時利用了圖像內的和圖像間的信息，極大地超越了之前的基于單訓練批次（single batch based）的方法。甚至得到了與使用對比訓練的方法接近的結果，而相比之下本文方法只用了一半的訓練批次。
我們的方法表明多批次訓練是不必要的，并為未來的單批次無監督的研究打開了大門

introduction

無監督的視覺表示學習，或者說自監督學習，是一個存在已久的問題，試圖在沒有人類監督信號的情況下，得到一個通用特征提取器。這個目標可以通過精心設計不帶有標注的pretext task來訓練特征提取器來達成。

根據pretext task的定義，大多數主流的方法分兩類：圖像內（intra-image）的任務和圖像間（inter-image）的任務。圖像內的任務，包括colorization和jigsaw puzzle，設計一種一張圖像的變換，并訓練一個網絡學習這種變換。由于每次只有訓練批次本身需要前向傳播計算，所以我們將這些方法稱作單批次方法（single-batch methods）。這類任務只使用了一張圖片的信息就可以完成，這限制了特征提取器的學習能力。

最近幾年圖像間任務迅猛發展，要求網絡能夠辨別不同的圖像。對比學習現在很流行，因為它可以降低正對的特征表示之間的距離，并擴大負對的特征表示之間的距離。為了建構正對，訓練過程需要使用經過不同的數據擴增的另一批次的數據。由于每個訓練批次和它的擴增過的版本要同時進行前向傳播，我們將這些方法稱作雙批次方法（dual-batches methods）。這種方法在訓練過程中大大提升了對資源的需求，如何能夠設計一種有效的基于單批次的方法，達到與雙批次相仿的性能仍舊是個問題。

本文中，我們提出了一個使用Jigsaw聚類（Jig-Clu）來有效訓練無監督模型的框架。該方法結合了拼圖和對比學習的優點，利用圖像內部和圖像間的信息指導特征提取。它學習更全面的表達。

該方法在訓練過程中只需要一個單批，但與其他單批方法相比，結果有很大提高。它甚至可以達到類似的結果與雙批次方法，但相比只有一半的訓練批次。

jigsaw clustring task

在本文提出的JigClu任務中，同一批次內的每張圖片被分成不同的塊，它們被隨機打亂在被接在一起，來形成一個新的批次用作訓練。目標就是將這個被打亂的恢復為原圖，如圖一所示。不同于以往的Jigsaw Puzzle任務，原圖分成的塊是在整個批次內被打亂的，而非在單張圖像內。我們需要去預測的事每個塊屬于哪張圖片和每個塊在原圖中的位置。

我們使用蒙太奇（montage）圖像而非單個塊作為網絡的輸入。這個改動大幅提升了任務的難度，并為網絡提供了更多的有用的信息供學習。網絡需要辨識出一張圖像的不同部分，并識別出它們原來的位置從而從多蒙太奇（multiple montage）輸入圖像中恢復原圖。

這個任務使得網絡能夠圖像內和圖像間的信息，只需要通過對拼接后的圖像進行前向傳播，與其他對比學習的任務相比只使用了一半的訓練批次。

為了恢復來自交叉圖像的圖塊，我們設計了一個聚類分支和一個定位分支。如圖二所示，具體來說，我們首先將來自拼接圖像的全局特征圖解耦為每個圖塊的表示。然后這兩個分支對每個圖塊的特征表示進行操作。聚類分支是將這些圖塊分為幾簇，每個簇只包含來自同一張圖像的圖塊。另一方面，定位分支，以圖像不可知的方式（image agnostic manner）預測每個圖塊的位置。

有了這兩個分支的預測結果，JigClu問題就得以解決。聚類分支作為一個有監督聚類任務進行訓練，因為我們知道圖塊是否來自同一張圖像。定位分支可以看作是一個分類任務，其中每個圖塊會被分配一個標簽，以此來表示其在原圖中的位置。定位分支預測所有圖塊的這個標簽。

我們的方法得到了不錯的結果，是因為我們提出的任務會使模型學習到不同種類的信息。一開始，從一張拼接的圖像中辨識出不同的圖塊迫使模型去捕捉圖像內不實例級別（instance-level）的信息。這一級別的特征在其他的對比學習方法中是丟失了的。

進一步，從多個輸入圖像中聚類到不同的圖塊有助于模型在圖像中學習圖像級別（image-level）的特征。這時最近的一些方法得到高質量結果的關鍵。我們的方法保持了這一重要屬性。最后，將每個圖塊擺放到正確的位置又要求細節的定位信息，這時之前的單批次方法考慮到的。但是在最近的一些方法中被忽略了。我們認為這種信息對于進一步提升結果來說仍舊是重要的。

performance of our method

通過我們的方法進行學習，可以產生圖像內的和圖像間的信息。這樣綜合的學習可以帶來一些優勢（spectrum of superiority）。首先，我們的方法在訓練階段只有一個批次，在Imagenet-1k的線性評估階段比其他單批次方法高了2.6%。 。。。

related work

handcrafted pretext tasks

訓練無監督模型的pretext task的方法有很多種。 將破壞過的圖像進行恢復是一個重要主題，有with tasks of descriminating synthetic artifacts [18], colorization [20, 43], image inpainting [31], and denoising auto-encoders [37], 等。另外，許多方法通過一些變換生成persuade labels（？）來訓練網絡。應用包括預測兩個塊的關系，解決jigsaw puzzle，還有識別被替代的類。[]是一個進階版的jigsaw puzzle，利用更復雜的方法選擇圖塊。視頻信息在訓練無監督模型時也很常用。

contrastive learning

我們的方法和對比學習也高度相關，首先由[]提出，根據[]可以得到更好的性能。最近[]，使用不同的擴增方法構建對比對取得了巨大的成功。尤其是，[]在pixel水平上利用圖像間和圖像內的信息。我們注意到訓練多批次圖像的對比學習方法需要大量的訓練資源。通過新穎的在單批次內設計對比對，我們的工作解決了這個問題。

jigsaw clustering

本章，我們會給出本文所提出的任務的定義。我們使用一個很簡單的網絡，只需要對原始的骨干網絡進行一點點調整。最后，我們設計了一個新穎的損失函數來更好地適應我們的聚類任務。

the jigsaw clustering task

在一個批次 $\mathbf{X}$$=x_1,x_2,\dots ,x_n$ 內，有 $n$ 個隨機選擇的圖像。每張圖像 $x_i$ 被分為 $m\times m$ 個圖塊。共有 $n\times m\times m$ 個圖塊。所有這些圖塊會被隨機重新排列來形成一組有蒙太奇圖像${\mathbf{X}}^{\prime }$$=x_1^{\prime },x_2^{\prime },\dots ,x_n^{\prime }$ 形成的新的批次。每張新圖同樣包含 $m\times m$ 個圖塊，這些圖塊來自不同的原批次 $\mathbf{X}$ 中的圖像。

任務就是對新批次 $\mathbf{X}$ 中的這 $n\times m\times m$ 個圖塊進行聚類為 $n$ 個簇，并且對同一簇的 $ m\times m$ 個圖塊預測位置來恢復出 $n$ 張原圖，整個過程見圖1。

本文提出的任務的關鍵是使用蒙太奇圖像作為輸入而不是每單獨一個圖塊。值得注意的是，直接使用小圖塊作為輸入會導致solution只有全局信息。此外，小尺寸的輸入圖像在許多應用中并不常見。僅在此處使用它們會引發pretext task和其他下游任務之間的圖像分辨率差異問題。這也可能導致性能下降。而簡單地直接擴展小圖塊將極大地提升訓練資源。

我們將蒙太奇圖像作為輸入完美地避免了這些問題。首先，來自一個批次的輸入圖像與原批次有著相同的尺寸，這和最近的方法相比只消耗了一半的資源。更重要的是，為了更好地完成本任務，網絡需要學習細節的圖像內的特征，來辨別一張圖像中的不同圖塊，和全局的圖像間的特征來將來自同一張原圖的不同圖塊聚集在一起。我們觀察到全面特征的學習大幅加速了特征提取了的訓練。更多實驗結果見下一節。

在本方法中，分圖像的方法是很關鍵的。$m$ 的選擇影響到任務的難度。我們的在ImageNet子集上的消融實驗顯示 $m=2$ 時得到最好的結果。我們推測 $m$ 過大會呈指數級地增加復雜度，使得網絡不能高效地學習。另外，我們觀察到將圖像切割為不連接的圖塊（disjoint pathches）并不是最優的。如圖3所示，隨著交叉點的延伸，網絡學習到更好的特征。這時可以解釋的，因為某些圖像的不同區域過于多樣化。如果沒有任何重疊的跡象，它們會給學習帶來困難。第5節會有更多解釋。

network design

我們為本任務設計了一個新的解耦網絡。首先是特征提取器，可以是任何網絡[]。然后有一個無參數的解耦網絡來將特征分為 $m\times m$ 個部分，對應同一個輸入圖像的不同的塊。然后用一個MLP來嵌入每個塊的特征，用作聚類任務；一個全連接層用來做定位任務。

解耦模塊首先將主干的特征映射插值為邊長為 $m$ 的倍數的新特征映射。我們是擴大特征圖而非縮小從而避免信息丟失。舉個例子，比如ImageNet，輸入尺寸都是224x224.如果用ResNet-50作骨干網絡，則提取到的特征是空間尺寸是 7x7的。如果 $m=2$ ，我們就將特征圖用雙線性插值搭配8x8。這樣特征圖的長度就是 $m$ 的倍數，我們可以使用平均池化，來對特征圖進行降采樣到 $n\times m\times m\times \hat{c}$ 。這樣，一個batch的就被分解為 $(n\times m\times m)\times \hat{c}$ ，即有 $(n\times m\times m)$ 個維度為 $\hat{c}$ 的向量。

然后每個向量都經過兩層MLP嵌入到長度為 $c$ ，來形成一組向量 $\mathbf{Z}=z_1,z_2,\dots ,z_{nmm}$ 用作聚類任務。同時， $(n\times m\times m)\times \hat{c}$ 的向量還會被送到一個作為分類器的全連接層，產生logits $\mathbf{L}=l_1,l_2,\dots ,l_{nmm}$，來完成定位任務。

我們的網絡是相當高效的，這個額外的解耦模塊是不需要參數的。與近期的工作相比，取一批的計算方法基本相同，訓練時只需取一批。這大大降低了訓練成本。

loss functions

聚類分支是一個有監督聚類任務，因為 $m\times m$ 個塊來自同一類。有監督聚類任務很方便，我們使用對比學習來實現。我們將聚類的目標是將來自同一類的物體（塊）拉到一起，將來自不同類的圖塊推開。我們使用余弦相似度來測量塊之間的距離。這樣來自同一簇的每一對塊，損失函數如下：
$${?}_{i,j}=?log\frac{exp(cos(z_i,z_j)/\tau )}{{\sum }_{k=1}^{nmm}{1}_{k=i}exp(cos(z_i,z_j)/\tau )}$$
其中 $1$ 表示指示函數（indicator function），$\tau$ 是溫度系數，用來平滑或者加劇距離。最終的所有來自同一簇的圖塊對的損失函數可寫作：
$${\mathcal{L}}_{clu}=\frac{1}{nmm}\sum _i(\frac{1}{mm?1}\sum _{j\in C_i{?}_{i,j}})$$
其中 $C_i$ 表示同一簇 $i$ 內的圖塊的索引 。

定位分支被視作是一個分類任務，損失函數是簡單的交叉熵損失，寫作：
$${\mathcal{L}}_{loc}=CrossEntropy(\mathbf{L},{\mathbf{L}}_{\mathbf{g}\mathbf{t}})$$
我們提出的Ji個C路的總體損失則為：
$$\mathcal{L}=\alpha {\mathcal{L}}_{clu}+\beta {\mathcal{L}}_{loc}$$
在我們的實驗中，$\alpha =\beta =1$ 即可得到好的結果。