Positional Encodings in ViTs 近期各視覺Transformer中的位置編碼方法總結及代碼解析

最近CV領域的Vision Transformer將在NLP領域的Transormer結果借鑒過來，屠殺了各大CV榜單。對其做各種改進的頂會論文也是層出不窮，本文將聚焦于各種最新的視覺transformer的位置編碼PE（positional encoding）部分的設計思想及代碼實現做一些總結。

ViT

[2021-ICLR] AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE

論文：https://arxiv.org/abs/2010.11929

代碼：https://github.com/lucidrains/vit-pytorch/blob/main/vit_pytorch

對于原始的ViT，筆者曾做過一份較為全面的代碼解析及圖解：Vision Transformer（ViT）PyTorch代碼全解析（附圖解），有興趣的讀者可以參考。

論文中的位置編碼方法

PE的設計

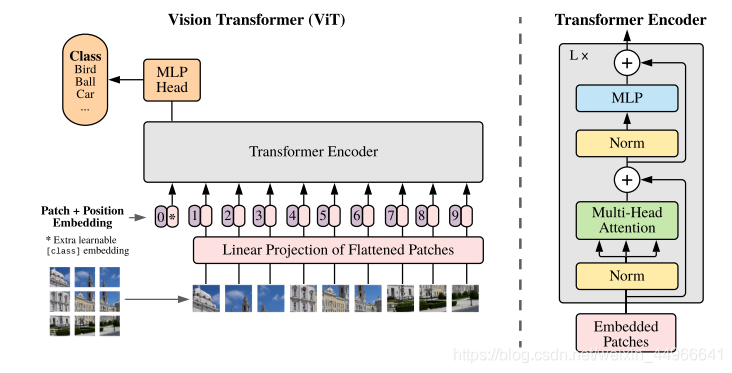
在ViT中，并沒有對位置編碼做過多的設計，只是使用一組可學習的參數來學習位置編碼，注意這樣的位置編碼如果在面對測試時的高分辨率圖像時是無法處理的。

ViT原文是這么說的：

When feeding images of higher resolution, we keep the patch size the same, which results in a larger effective sequence length. The Vision Transformer can handle arbitrary sequence lengths (up to memory constraints), however, the pre-trained position embeddings may no longer be meaningful. We therefore perform 2D interpolation of the pre-trained position embeddings, according to their location in the original image. Note that this resolution adjustment and patch extraction are the only points at which an inductive bias about the 2D structure of the images is manually injected into the Vision Transformer.

大概意思就是：當輸入高分圖像時，會導致序列的長度變長，ViT是可以處理任意長度的，但此時訓練得到的位置編碼就不再有意義了，并且只能通過2D插值實現。

$$\mathbf{z}=[{\mathbf{x}}_{class};{\mathbf{x}}_p^1\mathbf{E},{\mathbf{x}}_p^2\mathbf{E},\dots ;{\mathbf{x}}_p^N\mathbf{E}]+{\mathbf{E}}_{pos},\mathbf{E}\in {\mathbb{R}}^{(P^2?C)\times D},{\mathbf{E}}_{pos}\in {\mathbb{R}}^{(N+1)\times D}(1)$$
根據原文公式（即上式），ViT中位置編碼的維度應該為 $(N+1)\times D$ ，這里 $N$ 是圖塊的個數，+1是加上class token， $D$ 是映射后的每個token的維度，因為要直接相加，所以要保持一致。下面會用代碼來驗證查看。

關于PE的消融實驗

原文附錄中的實驗也顯示肯定是有位置編碼比沒有效果要好，但是看起來比較有設計的二維位置編碼和相對位置編碼相較于簡單的一維位置編碼性能反而更差。

第一行是完全沒有位置編碼，即沒有提供位置信息，相當于將一堆patch直接輸入進去；第二行是一維位置編碼，即將輸入patch看作是序列；第三行是二維位置編碼，將輸入看作是二維的patch網格；第四行是相對位置編碼，考慮到patch之間的相對距離，將空間信息編碼為而不是其絕對位置。

注意：如果要使用相對位置編碼，一定要考慮好自己的任務需不需要絕對位置信息，如目標檢測，由于要輸出預測的邊界框的坐標，因此絕對位置信息是必須的，這時使用相對位置編碼就不合適了。

關于PE的可視化實驗

ViT原文對位置編碼做的可視化實驗如下圖所示，熱力圖的含義是某個位置的圖塊的位置編碼與全圖其他位置圖塊的位置編碼的余弦相似度。我們可以看到，當然與自己相似度最高，然后就是同行同列也比較高，其他的位置就低一些，這也基本符合我們對位置編碼的基本期望，因為所謂的位置編碼要的就是圖像塊在原圖中的位置信息，更通俗點說就是行列信息，即某個圖像塊是在原圖中的哪行哪列。

代碼分析

ViT代碼中的位置編碼：

self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))	
# ...
x += self.pos_embedding[:, :(n+1)] 		

直接用可學習的參數torch.Parameter()作為位置編碼直接加到token序列中，跟隨整個訓練過程一起學習。（關于torch.Parameter()的介紹可見博客：PyTorch中的torch.nn.Parameter() 詳解）

另外，我們再用代碼來檢查一下ViT中的位置編碼的維度形狀，這里我們直接借用timm庫中的實現：

import timm
model = timm.create_model('vit_base_patch16_224', pretrained=True, num_classes=10)
pos_embed = model.state_dict()['pos_embed']
print(pos_embed.shape)         

輸出：

torch.Size([1, 197, 768])

我們是將224x224的圖像分為14x14個圖塊，共196塊，再加上class token 為197，而768則是我們指定的維度，符合我們的預期。

CPVT

Conditional Positional Encodings for Vision Transformers

論文：https://arxiv.org/abs/2102.10882

代碼：https://github.com/Meituan-AutoML/Twins （原文中給的鏈接中沒有實做代碼，實做代碼發布在這個倉庫了）

論文中的位置編碼方法

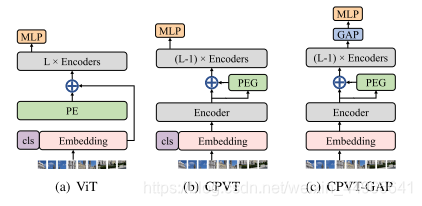
CPVT與ViT的位置編碼的區別在下圖中體現的很明顯，ViT的位置編碼PE沒有過多的設計，直接加到patch token和cls token得到的embedding上，然后就送到后面的多個transformer block（圖中encoder）中，注意ViT中的PE必須顯示地指定好token序列的長度。而CPVT則是先不加PE，在第一個transformer block之后，僅過PEG（Postional Encoding Generator）來生成位置編碼，在加到第一層的輸出上，在進行后面的計算，這樣長度就不需要顯式指定，可以隨輸入變化而變化，因此被稱為隱式的條件位置編碼。

其中的PEG模塊是用來產生條件位置編碼的模塊，其框架如下圖所示：

在 PEG 中，將上一層 Encoder 的 1D 輸出變形成 2D，再使用 F 學習其位置信息，最后重新變形到 1D 空間，與之前的 1D 輸出相加之后作為下一個 Encoder 的輸入。

具體來說，在上圖中，為了根據局部領域，我們首先將DeiT flatten過的輸入序列 $X\in {\mathbb{R}}^{B\times N\times C}$? reshape回二維圖像空間 $X^{\prime }\in {\mathbb{R}}^{B\times H\times W\times C}$? 。然后某個函數 $\mathcal{F}$? 會反復作用于 $X^{\prime }$? 中的局部圖塊來生成條件位置編碼 $E^{B\times H\times W\times C}$? ，PEG可以由二維卷積高效地實現，其卷積核 $k>=3$?，并且有零填充 $\frac{k?1}{2}$? 。注意這里的零填充是很重要的，它可以使模型感知到絕對位置， $\mathcal{F}$? 可以是多種形式，比如可分離卷積。

代碼分析

在CPVT的代碼實現中，我們主要來看PEG部分：

class PosCNN(nn.Module):def __init__(self, in_chans, embed_dim=768, s=1):super(PosCNN, self).__init__()self.proj = nn.Sequential(nn.Conv2d(in_chans, embed_dim, 3, s, 1, bias=True, groups=embed_dim), )self.s = sdef forward(self, x, H, W):B, N, C = x.shapefeat_token = xcnn_feat = feat_token.transpose(1, 2).view(B, C, H, W)if self.s == 1:x = self.proj(cnn_feat) + cnn_featelse:x = self.proj(cnn_feat)x = x.flatten(2).transpose(1, 2)return xdef no_weight_decay(self):return ['proj.%d.weight' % i for i in range(4)]

可以看到，與原文中對PEG的介紹一致：將第一層Encoder 的1D 輸出變形成 2D，再使用F學習其位置信息，最后重新變形到 1D 空間，與之前的 1D 輸出相加之后作為下一個 Encoder 的輸入。

這里的self.proj就是文中的轉換函數 F?。

我們再來看PEG模塊在整個CPVT中的使用：

class CPVTV2(PyramidVisionTransformer):def __init__(self, ...)# ...self.pos_block = nn.ModuleList(			# 實例化一個PEG模塊[PosCNN(embed_dim, embed_dim) for embed_dim in embed_dims])# ...def forward_features(self, x):B = x.shape[0]for i in range(len(self.depths)):x, (H, W) = self.patch_embeds[i](x)x = self.pos_drops[i](x)for j, blk in enumerate(self.blocks[i]):x = blk(x, H, W)if j == 0:x = self.pos_block[i](x, H, W)  # PEG模塊 在這里使用if i < len(self.depths) - 1:x = x.reshape(B, H, W, -1).permute(0, 3, 1, 2).contiguous()x = self.norm(x)return x.mean(dim=1) 

可以看到，只有在第一個encoder之后（for循環中j=0時），使用PEG模塊計算位置編碼，后面正常進行其他的其他Encoder的計算，與論文原文一致。

本文將保持持續更新，讀者如果遇到有趣的Vision Transformer的改進方法，也歡迎分享討論。