[2021-ICCV] MUSIQ: Multi-scale Image Quality Transformer 論文簡析

論文：https://arxiv.org/abs/2108.05997

代碼：https://github.com/google-research/google-research/tree/master/musiq

概述

當前SOTA的IQA（圖像質量評估）模型都是基于CNN的，基于CNN的模型通常受到在一個批次內，圖像尺寸必須固定的限制，所以其輸入圖像通常會進行縮放或者裁剪，當然這會導致圖像質量的下降。為了解決這個問題，本文設計了一個多尺度的圖像質量transformer（multi-scale image quality transformer）來處理不同尺寸、不同長寬比的原分辨率圖像。通過多尺度的圖像表示，本文的模型可以捕捉到不同粒度（granularity）的圖像質量。另外，本文提出了一種新型的基于哈希的（hash-based）二維空間嵌入方法和一種尺度嵌入，來作為多尺度表示中的位置嵌入。

上圖中右側(b)圖是傳統的CNN模型的做法，必須要縮放或者裁剪來固定輸入圖像尺寸，而這無疑會影響原圖的圖像質量；而左側(a)圖則是本文的多尺度圖像質量transformer，基于圖像塊可以以多尺度的形式直接處理原圖。

另外，由于MUSIQ只改變輸入編碼，因此它可以適應任何transformer變體，也就是說，本文提出的創新點是在編碼階段的處理方法，得到輸入編碼之后可以放到Swin、CvT之類的新型transformer里都是可以的。

本文的創新點總結如下：

1. 本文提出一種基于圖像塊的多尺度圖像質量transformer（multi-scale image quality transformer MUSIQ），可以處理不同尺寸、不同長寬比的全尺寸輸入圖像，并且可以提取多尺度的特征。
2. 本文提出了一種新型的基于哈希的（hash-based）二維空間嵌入方法和一種尺度嵌入，來幫助transformer捕獲空間間和尺度間的信息。
3. 本文提出的MUSIQ在四個大規模IQA數據集上取得SOTA性能。

方法

模型框架

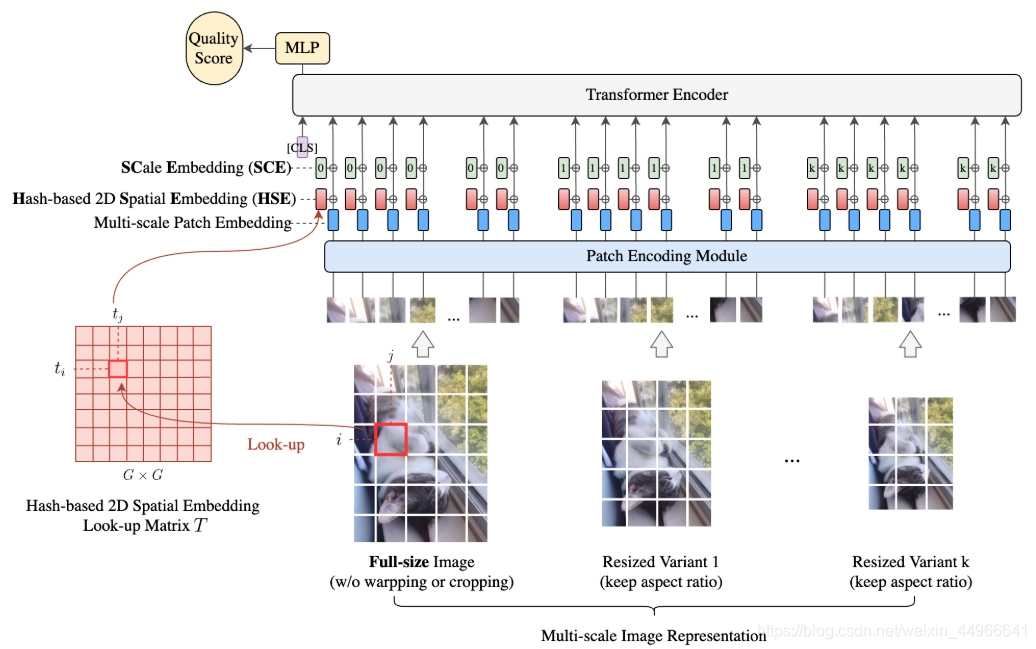
MUSIQ的整體結構如上圖所示，首先得到輸入圖像的多尺度表示，包括原圖和固定長寬比縮放（ARP(aspect ratio preserved) resized）的變體。不同尺度的圖像被分成固定大小的圖像塊，然后被送入到模型中，由于圖像塊是來自不同的空間分辨率的圖像，我們需要高效地將這些多種長寬比、多種尺度的輸入編碼為一個token序列，捕獲像素、空間和尺度信息。

為此，本文設計了三個編碼模塊：

1. 圖像塊編碼模塊
2. 基于哈希的空間嵌入模塊
3. 可學習的尺度嵌入

分別對來自多尺度圖像的圖像塊本身、每個圖像塊的二維空間位置、不同的尺度進行編碼。

在將多尺度的圖像輸入編碼為一個token序列之后，我們先準備一個額外的可學習的分類頭classification head（CLS）。transformer encoder輸出中的CLS token將作為最終的圖像表示。然后在最后加一個全連接層來預測圖像質量分。由于MUSIQ只改變輸入編碼，因此它可以適應任何transformer變體，也就是說，本文提出的創新點是在編碼階段的處理方法，得到輸入編碼之后可以放到Swin、CvT之類的新型transformer里都是可以的。

多尺度圖像塊嵌入

ARP resize = aspect ratio preserved resize 即固定長寬比縮放，后面不在贅述，直接簡稱ARP resize。

為了同時捕獲局部信息和全局信息（各種多尺度方法的老說辭了^^），本文提出對圖像的多尺度表示進行建模。

記全尺寸原圖的高、寬、通道數分別為 $H,W,C$， 使用高斯核對全尺寸原圖進行ARP resize（保持長寬比的縮放）之后的多尺度圖像的高、寬、通道數分別為 $h_k,w_k,C$ ，其中 $k=1,\dots ,K$ ，$K$是每個輸入的ARP resize變體的個數。為了將多尺度輸入對齊，從而有一致的全局視角，將每個多尺度變體的長邊固定為 $L_k$ ，從而：
$${\alpha }_k=L_k/max(H,W),h_k={\alpha }_{k}H,w_k={\alpha }_{k}W$$
${\alpha }_k$ 即為每個尺度的縮放因子。

從每個多尺度圖像中切分出尺寸為 $P$ 的正方形圖像塊。對于高、寬不是 $P$ 的整數倍的圖像，用零填充（這里筆者有個問題：既然都padding 0了，那不就相當于也將輸入的尺寸固定了嗎，既然可以padding，那什么網絡都能處理原尺寸圖像啊，沒搞懂這樣設計還有什么意義）。每個圖像塊被圖像塊編碼器模塊patch encoder module編碼為 $D$ 維的嵌入，$D$? 即為transformer中的隱層token尺寸。本文的patch encoder module使用了5層的ResNet而非線性映射。將patch encoder module輸出的圖像塊嵌入拼接起來就得到輸入圖像的多尺度映射序列，來自原尺寸圖像和ARP resize的多尺度圖像的圖像塊個數就分別為：$N=HW/P^2$，$n_k=h_k{w}_k/P^2$ 。

對于輸入圖像尺寸不同導致的 $N,n_k$ 不同，從而序列長度不同的問題。本文采用了NLP中常用的pad+mask的方式來得到固定長度的輸入，從而進行訓練。前面提到過ARP resize圖像的長邊固定在 $L_k$? ，因此有 $n_k<=L_k^2/P^2=m_k$ ，所以直接pad到 $m_k$ 即可。

基于哈希的二維空間嵌入

傳統的固定長度的位置嵌入無法適應可變分辨率的輸入，并且也無法對齊來自不同尺度但空間位置接近的圖像塊。

本文認為一個有效地適合MUSIQ的位置嵌入應當滿足以下條件：

1. 可以在不同長寬比、不同分辨率下有效地為圖像塊的空間信息進行編碼；
2. 不同尺度下空間位置接近的圖像塊應當有相近的空間嵌入
3. 便于實現，不會干擾到transformer attention

據此，本文提出了一種基于哈希的二維空間嵌入（HSE），記某個圖像塊的位置在第 $i$ 行，第 $j$ 列，被哈希到 $G\times G$ 的網格中的相應的元素。該網格中的每一個元素是一個 $D$ 維的嵌入向量。即有一個可學習的矩陣 $T\in {\mathbb{R}}^{G\times G\times D}$ ，輸入尺寸為 $H,W$ ，對于位置在 $(i,j)$ 的圖像塊，其空間嵌入被定義為 $T$ 中的 $(t_i,t_j)$ 位置的元素：
$$t_i=\frac{i\times G}{H/P},t_j=\frac{j\times G}{W/P}$$
將 $D$ 維的空間嵌入 $T_{t_i,t_j}$ 逐元素地加到patch embedding上。為了快速查找，將$(t_i，t_j)$四舍五入到最接近的整數。

為了在不同尺度之間對齊圖像塊，來自不同尺度的圖像塊都映射到一個同樣的表格 $T$。這樣，在空間上位置接近但是來自不同的尺度的圖像塊也會被映射到$T$中接近的嵌入上。因為$i$和$H$以及$j$和$W$與尺寸調整因子$\alpha$成比例變化。

$T$ 的尺寸 $G$ 存在一個trade-off，$G$? 過小會導致過多的哈希碰撞，從而使得模型無法分辨空間位置接近的圖像塊；過大則會導致浪費內存并且需要更多的分辨率來進行訓練。

尺度嵌入

由于本文對所用的圖像復用一個相同的哈希矩陣，HSE是無法分別來自不同尺度的圖像塊的，因此本文引入一個額外的尺度嵌入SCE來幫助模型分辨來自不同尺度的圖像塊。

本文將SCE定義為一個可學習的嵌入 $Q\in {\mathbb{R}}^{(K+1)\times D}$ ，因為輸入有 $K$ 個尺度的變體。$Q_0\in {\mathbb{R}}^D$ 逐元素地加到所有的 $D$ 維的原分辨率圖像的pathch embedding上，$Q_k\in {\mathbb{R}}^D$ 分別逐元素地加到所有 $k$ 尺度的patch embedding上。

預訓練和微調

本文預訓練還是在ImageNet上做的，預訓練階段會使用各種數據增廣的方法來提升性能。

微調則是在圖像質量和美學質量數據集上進行，在微調階段，保持原尺寸圖像作為輸入，數據增廣只采用對圖像質量無影響的水平翻轉。

實驗

吊打友商部分的實驗就不在這里說了，具體指標大家可以到原文中去看。我們主要看一下和方法本身有關的消融實驗和可視化實驗。

ARP的重要性

本實驗旨在說明固定長寬比縮放(ARP)的重要性，上面幾個CNN和ViT的方法是直接介紹384/224的正方形square resize的輸入，對于本文多尺度方法分別做了正方形square resize的的多尺度輸入，和保持原圖長寬比的多尺度輸入。實驗結果成功證實了保持長寬比在圖像質量評估中的重要作用。

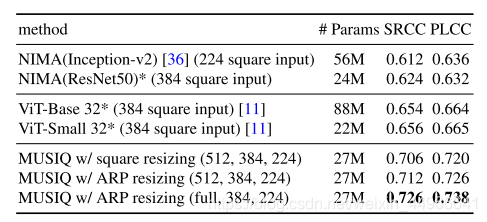
除此之外，作者還用折線圖配合一張圖像破壞長寬比的形式直觀地展現了ARP的作用。圖中藍線，即帶ARP的本文方法對圖像長寬比的變化非常敏感，可以敏銳地察覺到圖像長寬比變化對圖像質量的影響。而其他在訓練時接收的事固定正方形輸入的模型則感知不到這種長寬比的變化帶來的影響。

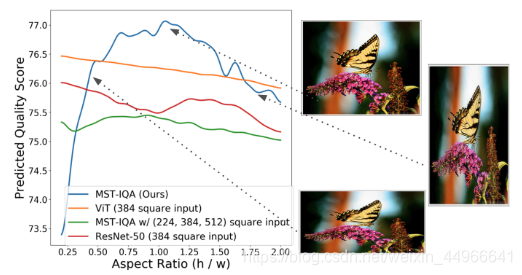
多尺度結合的全尺寸輸入的有效性

本實驗展示的是多尺度、全尺寸輸入的有效性。實驗結果如下表，可以看到多尺度輸入性能優于單一尺度輸入 ，原尺寸輸入（full）性能優于固定尺寸輸入，并且多尺度結合訓練的性能也比多個尺度分別訓練再結合

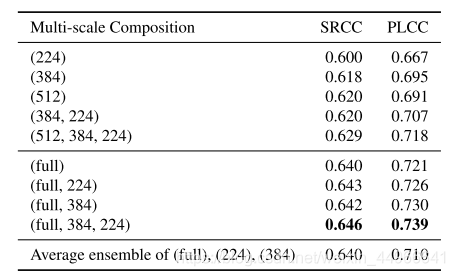
下面的注意力可視化實驗也說明了多尺度學習的作用（注意一下三列分辨率是不同的，這里為了展示縮放到同樣大小來適應表格）。可以看到在高分辨率的圖像中，模型更加關注細節信息；而在低分辨率的圖像中，模型更加關注全局信息。

下面是基于哈希的二維空間嵌入的每個網格位置 $(i,j)$ 與其他位置處嵌入的余弦相似度。空間位置嵌入是為了反應二維圖像的空間信息，通俗點說就是行列信息，即某個圖像塊在二維圖像的哪一行，哪一列。可以看到除了和自己的相似度最高之外，和同行同列的空間嵌入的相似度也較高。這時符合我們的預期的，說明二維空間嵌入可以準確地表征圖像塊的行列信息。

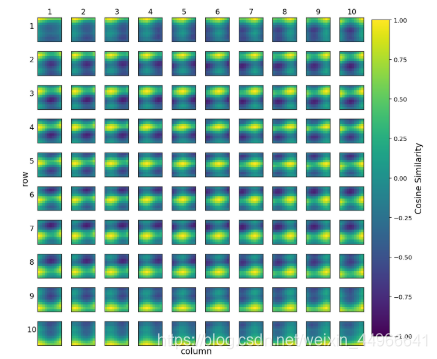
基于哈希的空間嵌入和尺度嵌入的有效性

正文最后一個消融實驗對比了有無本文的基于哈希的空間嵌入和有無尺度嵌入的情況下的模型的性能表現。可以看到，這兩個嵌入是必需的。

還有一個實驗對比了不同的圖像塊編碼模塊，還是本文的方法較優。

本文的概述、方法和實驗就簡單地介紹到這里，已經囊括方法思路和大部分細節及正文實驗，此外還有一些附錄實驗，有興趣的話請移步到原文中查看。