第2章線性表的基本使用及其cpp示例（第二章匯總,線性表都在這里）

2.1線性表的定義和特點

【類型定義：
*是n個元素的有限序列
*除了第一個元素沒有直接前驅和最后一個沒有直接后驅之外，其余的每個元素只有一個直接前驅和直接后驅；
（a1,a2…an）

【特征：
*有窮性：由有限個元素組成，元素個數表長度 n=0空表
（a1,a2…an），稱下標i為線性表的位序

*有序性： 線性表元素之間存在嚴格次序關系（序偶關系）

*同一性：線性表屬于同類數據元素組成，每一個元素都屬于同一數據對象
eg：（A，12，b）不是線性表，不遵守同一性

2.1.2線性表抽象數據類型定義

ADT List{

//數據對象
D={ai|ai∈ElemSet,i=1,2…n, n>0}

//數據關系
R1={<ai-1,ai>|ai-1,ai∈D,i=2,…n}

//基本操作
1)InitList(&L)
將：初數化為空表
2）

…

}ADT list

【引用在什么情況下使用】

所用到的元素，哪個元素變化（帶入數據或者 ），就在此元素前加 &
【eg】
1)InitList(&L)
將：初數化為空表
//表L初始化帶入值，發生變化，故早L前加&

2.1.5 示例 *有序集合的合并

有序表：LA和LB，求合并遞減有序LC

基本思路：
{若ai<=bi,則ci=bi
{
{若bi<ai,則ci=ai
//誰小就先吧他賦給c

算法時間復雜度：O（ListLength(LA)）+O（ListLength(LB)）

2.2.1線性表的順序表示和實現------順序映像

【順序存儲】在【查找時】的時間復雜度為【O(1)】，因為它的地址是連續的，只要知道首元素的地址，根據下標可以很快找到指定位置的元素
【插入和刪除】操作由于可能要在插入前或刪除后對元素進行移動，所以順序存儲的時間復雜度為【O(n)】。

1）初始化操作
思想：構造一個空表
設置表起始位置、表長及可用空間

#define LIST_INIT_SIZE 100
#define LISTINCREAMENT 10
typedef struct
{
ElemType *elem;   //定義個地址變量，使其后面能指向線性表占用的數組空間
int length;  // 線性表的長度
int listsize;  // 當前分配的存儲容量
}SqList;//初始化操作
Status InitList_Sq(SqList &L)  //初始化
{ //構造一個空表
L.elem=(ElemType)malloc(LIST_INIT_SIZE*size of(ElemType));
if(!L.elem)  exit(OVERFLOW);  //存儲分配失敗
L.length=0;   //空表長度為0
L.listsize=LIST_INIT_SIZE;  //初始存儲容量
return OK;}

2.2.3順序表的插入

2）順序插入操作

目的：在線性表L第i個元素前插入一個元素e

【基本思想
1）判斷i是否在允許范圍
2）存儲空間是否已滿
3）將第i個元素和后面的所有元素向后移動
4）新元素寫在空出的第i個位置
5）線性表長度加1

【注意】
長度為n的順序表第i個位置插入移動n-i+1個元素


Status ListInsert_Sq(SqList&L,int i,ElemType e){if(i<1||i>1.lenth+1)
return ERROR;   //插入位置不合法if(L.length>=L.listsize)
{
newbase=(ElemType*)realloc(L.elem,(LIST_INIT_SIZE+LISTINCREMENT)*sizeof(ElemType)); If(!newbase) exit（OVERFLOW）;// 當前存儲空間已滿L.elem=newbase;              //新基址L.listsize+=LISTINCREMENT;  // 增加存儲容量 
}     //判斷空間足夠q=&(L.elem[i-1]);   //q指向插入位置for(p=&(L.elem[L.elem-1]);p>-q;--q)
*(p+1)=*p;
*q=e;
++L.length;
return OK;
}

2.2.4順序表的刪除和插入

【基本思路
1）判斷i是否在允許范圍
2）將線性表的第i個元素給e
3）將第i個元素和后面的所有元素向前移動一個位置
4）線性表長度減1


Status ListDelete_Sq(SqList&L,int i,ElemType e){//刪除第i個元素并用e返回值if(i<1||i>1.lenth+1)
return ERROR;   //刪除位置不合法p=&(L.elem[i-1]);   //q指向插入位置
e=*p;
q=L.elem+L.length-1; //表尾元素位置
for(++p;p<=q;++p)
*(p-1)=*p;    //p-1指向p--L.length;
return OK;
}

【圖】：平均移動次數

【查找操作】11:42

int LocateElem_Sq(SqList,ElseType e)
{
//查詢第一個 滿足條件的元素，若存在，返回位序，否則返回0；
int i;
i=1;
while (i<=L.length&&L.elem[i-1]!=e)
++i;
if(i<=L.length)
return i;
else return 0;
}// locateElem_Sqi<=L.length&&L.elem[i-1]!=e
i>L.length

【順序結構優缺點14:15
【優點：
邏輯相鄰，物理相鄰
可隨機存取一元素
存儲空間使用緊湊
【缺點：
插入，刪除需要移動大量元素
預先分配空間需按最大空間分配，利用不充分表難以擴充

【】線性表的合并問題
【圖：例1】
基本思路：
1）初始化Lc為空表
2）分別從La和Lb取得當前元素ai和bi
3)若ai<bj，則將ai插入到Lc中，否則
bj插入到Lc中

代碼：


Viod MergeList(SqList La.SqList ,lb.SqList &Lc)
{
Pa=La.elem;
Pb=Lb.elem;
Lc.listsize=Lc.length=La.elem+Lb.elem;
Pc=Lc.elem=(ElemType*)malloc(Lc.listsize* sizeof(ElemType));
if(!Lc.elem)
exit(overflow);
Pa_last=La.elem+La.length-1;
Pb_last=Lb.elem+Lb.length-1;
while(pa<=pa_last&&pb<=pb_last)
{
if(*pa<= *pb)
*pc++= *pa++;
else
*pc++= *pb++;
}
while(pa<=pa_last)
*pc++= *pa++;
while (pb<=pb_last)
*pc++= *pb++;
}

2.3線性表的鏈式表現與實現

2.3.1.1單鏈表
【特點：
*用一組任意的存儲單元存儲線性表的數據元素
*利用指針實現用不同相鄰的存儲單元存放邏輯上相鄰的元素
*每個元素ai，除存儲本身信息外，還存儲其直接后繼的元素（后一個元素的地址）
*結點：數據元素ai的存儲映像
{數據域：數據元素本身
指針域：指示直接后繼的存儲位置

【頭指針、頭結點、第一個元素結點
*頭指針：以線性表的第一個數據元素a1的存數地址作為線性表的地址，稱為線性表的頭指針

*頭結點：為了操作方便，在第一個結點前虛加一個“頭結點”，指向頭結點的指針為鏈表的頭指針（相當于第一個呀元素的結點）

代碼：

typedef struct LNode{ElemType data;struct LNode*next;
}LNode,*LinkList    //LNode是結構體的別名，LinkList為指針變量
//相當于：typedef LNode *LinkList

2.3.1.2 單鏈表存儲結構實現

格式： data | next

【p指向數據域
(*p).data=10;
或：p->data=10; //表示p指向結點的數據域

（*p）.next=10
或 p->next //表示p指向結點的指針域

*生成一個LNode型新結點：
p=(LinkList)malloc(sizeof(LNode));

*系統回收p的結點
free（p）

*單鏈表特點：
1）是它是一種動態結構，整個存儲空間為多個鏈表共用
2）不需預先分配空間
3）指針占用額外存儲空間
4）不能隨機存取，查找速度慢

【基本操作：
1）GetElem（L,i,&e） //第i個元素用e帶回結果
2）ListInsert(&L,i,e) //插入
3）ListDelete(&L,i,e) //刪除
4）CreateList_L（&L,n） //創建線性表

2.3.1.3單鏈表的查找

【操作：
1）GetElem（L,i,&e）

【基本思想：
1）令p為指針變量，首先指向第一個結點，變量 j為計數器
2）依次向后查找，循環結束條件：p為空或j>=i；
3）找到用e返回第i個值

【代碼：


Status GetElem_L(LinkList L,int i,ElemType&e)
{  //L是鏈表的頭指針（對帶頭結點的鏈表），以e返回dii個值
p=L->next;
j=1;while (p&&j<i)
{p=p->next;  ++j;if(!p||j>i)return ERROR;e=p->data;  //取第i個值
return OK;
}

2.3.1.4單鏈表的插入操作

2）ListInsert(&L,i,e)
在線性表第i個元素之前插入一個元素e，元素e存在結點s中

【思路：在第i項的前加一個接結點，i-1項的地址域和e的數據域連接


int ListInsert_L(LinkList&L,int i,int e)
{
LNode*p,*s;int j;   //或：LinkList p,s;    等同
p=L;j=0; //計數器
while(p&&j<i-1)
{p=p->next;++j;}
if(!p||j>i-1)
return ERROR;
s=LinkList()malloc(sizeof(LNode)); //新結點
s->data=e;
s->next=p->next;
p->next=s;
return OK;
}

2.3.1.5 單鏈表的刪除

【思路：刪除第i個元素，并保存到元素e中

【代碼：

int ListDelete_L(LinkList&L,int i,ElemType&e)
{
LNode*p,*q;int j;
p=L;j=0;
while(p->next||j<i-1)       //？？？？我覺得應該是(!p||j>i-1)
{p=p->next;++j}
if(p->next==NULL||j>i-1)
return ERROR;    //刪除位置不合理
q=p->next;  //q指向被刪除結點
p->next=q->next;  //
e=q->data;   //取出第i個結點的數據域
free(q);    // 釋放dii個結點的內存
return OK;
}

2.3.1.6單鏈表的建立

【頭插法建立有頭結點的單鏈表
可理解為:每次插一個新的頭
【圖】
L=(Linklist)malloc(sizeof(LNode)) //sizeof后面跟數據類型（LNode）
L->next=NULL

【圖】
p=(LinkList)malloc(sizeof(LNode))
scanf("%f",&(p->data)); //

【整個代碼：

void CreateList_L(LinkList &L,int n)
{
LNode*p;int i;
L=(LinkList)malloc(sizeof(Lnode));
L->next=NULL;
for(i=n;i>0;--i)
{ p=(Listlink)malloc(sizeof(LNode));
scanf("%d",&p->data);
p->next=L->next;
l->next=p     //這里的=都可以理解為“給了，到，指向”
}
}

2.3.1.7有序單鏈表的合并

例：線性表LA和LB中數據元素按照廢帝劍有序排列，將LA和LB合并為一個新的LC，且LC中的數據元素仍按照遞減有序排列

在這里插入圖片描述
【代碼：


void MergeList_L(LinkList&La,LinkList&Lb,LinkList&Lc)
{// 歸并La和Lb得到Lc，Lc也按照降序排列
LinkList pa,pb,pc;
pa=La->next;pb=Lb->next;
Lc=pc=La;  //用La的頭結點作為Lc的頭結點
while(pa&&pb)
{
if(pa->data<=pb->data)
{
pc->next=pa; pc=pa;pa=pa->next;
}
else
{
pc->next=pb;pc=pb;pb=pb->next;
}
pc->next=pa?pa:pb;  //若a不為空則指向pa，否則指向pb
free(Lb);
}

2.3.1.8靜態鏈表

定義：用數組描述的鏈表叫靜態鏈表

目的：為在不設指針類型的高級程序語言中使用鏈表結構

存儲結構：

#define MAXSIZE 100 //靜態鏈表最大長度
typedef struct{
ElemType data;
int cur;  //游標，代替指針的結點，表示數組中的位置
}component,SLinkList[MAXSIZE]

在這里插入圖片描述

2.3.2循環鏈表

循環鏈表是單鏈表的變形

循環鏈表最后一個結點link指針部位NULL，而是指向表的前端

為簡化操作，在循環鏈表往往插入頭結點

特點：
只要知道表中一結點的地址，就可以搜索到所有其他結點的地址

操作的時間復雜度：
表尾插入，時間復雜度：O(1)
表尾刪除：O(n)
表頭插入，同表尾
表頭刪除：O(1)

2.3.3雙向鏈表 插入、刪除

指在前驅和后驅方向都能游歷（遍歷）的線性鏈表

雙向鏈表的每個結點有兩個指針域
【結構】：prior data next

雙鏈表通常采用帶頭結點的循環鏈表形式
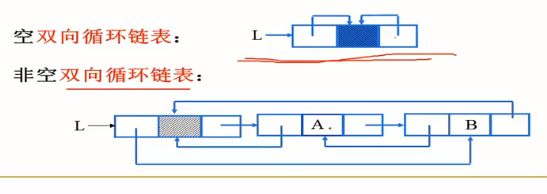
在這里插入圖片描述

可理解為首位相接的數據“圈”，每個結點都可以向前或向后走

【結點指向】
在這里插入圖片描述

【插入操作】：

1.分配空間
2.斷開與連接

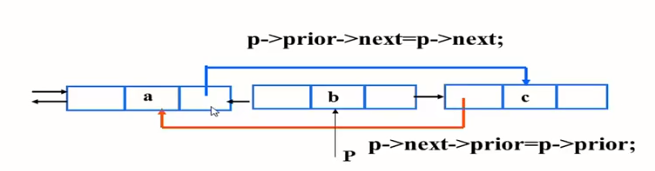
在這里插入圖片描述
【操作算法


status ListInsert_DuL(DuLinkList &L,int i,ElemType e)
{if(!p=GetElem_Dul(L,i))  
return ERROR;  //相當于嵌套第i個結點的指針if(!(s=(DuLinkList)malloc(sizeof(DuLNode))))
return ERROR   //空間分配失敗
s-data=e;      //將數據放入新結點的數據圖
s-prior=p-prior;  //將p的前驅結點指針放入新結點的前向指針域
s-next=p;      //將p放入新結點的反向指針域
p-prior-next=s;   //修改p的前驅結點的反向指針
p-prior=s;    // 修改p的前驅指針
return OK;
}   ListInsert_DuL
【刪除操作】

1.p指向目標結點
2.將目標結點的前一個結點與后一個連接（跳過中間那個）
3釋放內存

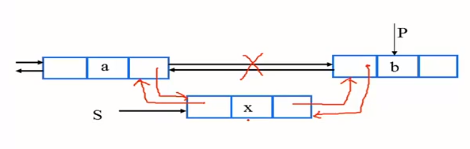
在這里插入圖片描述
【操作算法】
status ListDelete_Dul(DuLinkList &L,int i,ElemType &e)
{ 刪除頭結點的雙向循環鏈表L中第i個元素返回，1=i=表長
if（!p=GetElem_Dul(L,i)）
return ERROR; 查找第i個指針
e=p-data; 將p指向結點數據域中的值取出
p-prior-next=p-next; p前一個結點的后驅指向p的后一個結點
p-next-prior=p-prior; 后指向前
free§; 釋放p
return OK;

} ListDelete_DuL

【 算法評價：T(n)=O(n) 】

！注意：如何選擇合適的存儲結構
鏈表只能順序存取，在單鏈表的最后一個元素后插入元素，需遍歷整個鏈表

在這里插入圖片描述

頻繁插入刪除用鏈式存儲
偶爾 用順序存儲

2.4一元多項式的表示及相加

  • n階多項式的表示：
    n階多項式有n+1項
    指數按升冪排序

【 優點：

  • 多項式的項數可以動態增長，不存在存儲溢出的問題
  • 插入，刪除方便，不移動元素

【表示：
有兩個數據域，一個地址域

在這里插入圖片描述
【一元多項式的建立算法：


void polycreate(Polylist &head)
{
polylist rear,s;  int c,e;
head=(Polynode *)malloc(sizeof(POlynode));
rear=head;      //尾插法
scanf("%d,%d",&c,&e);
while(c!=0){ s=(Polynode *)malloc(sizeof(Polynode));s->coef=c; s->exp=e;rear->next=s;  rear=s;scanf("%d,%d",&c,&e);rear->next=NULL;}
}

【一元多項式相加：

  • 掃描兩個多項式
    {若當前被檢測項指數相等，系數相加。 和不為0，則結果加到結果多項式

    {若檢查指數不等，將指數小的加到結果多項式，然后往后移

  • 若一個多項式檢測完，將另一個多項式剩余全部復制到結果多項式

【設計思想：

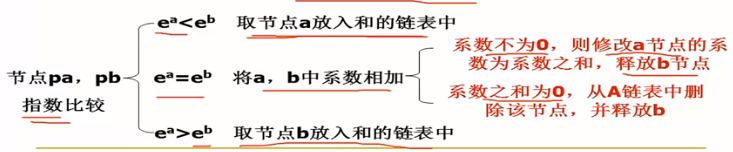
在這里插入圖片描述
算法：

void polyadd(Polylist polya,Polylist polyb)
{
Polynode *pa,*pb,*pc,*r;
int sum;
pa=polya->next;
pb=polyb->next;
pc=polyb;   //pre指向和多項式的尾結點while(pa!=NULL&&pb!=NULL)
{
if(pa->exp<pb->exp){pa->next=pa; pc=pa;pa=pa->next;}    //【1.】 pa指數小于pb指數，把pa給了pc
else if(pa->exp==pb->exp){sum=pa->coef+pb->cofe;if(sum!=0)                                            //【3.】指數相等，但系數sum不是0{pa->cofe=sum; pc->next=pa;pc=pa; pa=pa->next;r=pb; pb=pb->next ;  free(r);}else                                                    //【4.】指數相等，系數sum為0{r=pa; pa=pa->next;free(r);r=pb;pb=pb->next;free(r);}}else{pc->next=pb; pc=pb;pb=pb->next;}    // 【2.】pb指數小于pa指數，把pb給了pcif(pa!=NULL)pc->next=pa;
else pc->next=pb;
}}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/532680.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/532680.shtml
英文地址，請注明出處：http://en.pswp.cn/news/532680.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

TVM：通過Python接口（AutoTVM）來編譯和優化模型

TVM：通過Python接口（AutoTVM）來編譯和優化模型

TVM&#xff1a;通過Python接口&#xff08;AutoTVM&#xff09;來編譯和優化模型 上次我們已經介紹了如何從源碼編譯安裝 tvm&#xff0c;本文我們將介紹在本機中使用 tvm Python 接口來編譯優化模型的一個demo。 TVM 是一個深度學習編譯器框架&#xff0c;有許多不同的模塊…
閱讀更多...
TVM：在樹莓派上部署預訓練的模型

TVM：在樹莓派上部署預訓練的模型

TVM&#xff1a;在樹莓派上部署預訓練的模型 之前我們已經介紹如何通過Python接口&#xff08;AutoTVM&#xff09;來編譯和優化模型。本文將介紹如何在遠程&#xff08;如本例中的樹莓派&#xff09;上部署預訓練的模型。 在設備上構建 TVM Runtime 首先我們需要再遠程設備…
閱讀更多...
2.2線性表的順序表

2.2線性表的順序表

2.2.1線性表的順序表示和實現------順序映像 【順序存儲】在【查找時】的時間復雜度為【O(1)】&#xff0c;因為它的地址是連續的&#xff0c;只要知道首元素的地址&#xff0c;根據下標可以很快找到指定位置的元素 【插入和刪除】操作由于可能要在插入前或刪除后對元素進行移…
閱讀更多...
TVM：交叉編譯和RPC

TVM：交叉編譯和RPC

TVM&#xff1a;交叉編譯和RPC 之前我們介紹了 TVM 的安裝、本機demo和樹莓派遠程demo。本文將介紹了在 TVM 中使用 RPC 進行交叉編譯和遠程設備執行。 通過交叉編譯和 RPC&#xff0c;我們可以在本地機器上編譯程序&#xff0c;然后在遠程設備上運行它。 當遠程設備資源有限…
閱讀更多...
2.3單鏈表的基本使用及其cpp示例

2.3單鏈表的基本使用及其cpp示例

2.3線性表的鏈式表現與實現 2.3.1.1單鏈表 【特點&#xff1a; *用一組任意的存儲單元存儲線性表的數據元素 *利用指針實現用不同相鄰的存儲單元存放邏輯上相鄰的元素 *每個元素ai&#xff0c;除存儲本身信息外&#xff0c;還存儲其直接后繼的元素&#xff08;后一個元素的地址…
閱讀更多...
TVM：簡介

TVM：簡介

TVM&#xff1a;簡介概述 Apache TVM 是一個用于 CPU、GPU 和機器學習加速器的開源機器學習編譯器框架。它旨在使機器學習工程師能夠在任何硬件后端上高效地優化和運行計算。本教程的目的是通過定義和演示關鍵概念&#xff0c;引導您了解 TVM 的所有主要功能。新用戶應該能夠從…
閱讀更多...
2.3.3單鏈表的雙向鏈表

2.3.3單鏈表的雙向鏈表

2.3.3雙向鏈表 插入、刪除 指在前驅和后驅方向都能游歷&#xff08;遍歷&#xff09;的線性鏈表 雙向鏈表的每個結點有兩個指針域 【結構】&#xff1a;prior data next 雙鏈表通常采用帶頭結點的循環鏈表形式 可理解為首位相接的數據“圈”&#xff0c;每個結點都可以向前…
閱讀更多...
nvidia-smi 命令詳解

nvidia-smi 命令詳解

nvidia-smi 命令詳解 簡介 nvidia-smi - NVIDIA System Management Interface program nvidia smi&#xff08;也稱為NVSMI&#xff09;為來自 Fermi 和更高體系結構系列的 nvidia Tesla、Quadro、GRID 和 GeForce 設備提供監控和管理功能。GeForce Titan系列設備支持大多數…
閱讀更多...
2.4一元多項式的表示及相加，含cpp算法

2.4一元多項式的表示及相加，含cpp算法

2.4一元多項式的表示及相加 n階多項式的表示&#xff1a; n階多項式有n1項 指數按升冪排序 【 優點&#xff1a; 多項式的項數可以動態增長&#xff0c;不存在存儲溢出的問題插入&#xff0c;刪除方便&#xff0c;不移動元素 【表示&#xff1a; 有兩個數據域&#xff0c;一…
閱讀更多...
TVM：使用Tensor Expression (TE)來處理算子

TVM：使用Tensor Expression (TE)來處理算子

TVM&#xff1a;使用Tensor Expression (TE)來處理算子 在本教程中&#xff0c;我們將聚焦于在 TVM 中使用張量表達式&#xff08;TE&#xff09;來定義張量計算和實現循環優化。TE用純函數語言描述張量計算&#xff08;即每個表達式都沒有副作用&#xff09;。當在 TVM 的整體…
閱讀更多...
4-數據結構-串的學習

4-數據結構-串的學習

4.1串類型的定義 1.串&#xff1a;&#xff08;或字符串&#xff09; 串是由多個字符組成的有限序列&#xff0c;記作&#xff1a;S‘c1c2c3…cn’ (n>0) 其中S是串的名字&#xff0c;‘c1c2c3…cn’ 是串值 ci是串中字符 n是串的長度&#xff0c;表示字符的數目 空串&a…
閱讀更多...
Linux下rm誤刪恢復 extundelete

Linux下rm誤刪恢復 extundelete

Linux下rm誤刪恢復 extundelete 誤刪之后要第一時間卸載&#xff08;umount&#xff09;該分區&#xff0c;或者以只讀的方式來掛載&#xff08;mount&#xff09;該分區&#xff0c;否則覆寫了誰也沒辦法恢復。如果誤刪除的是根分區&#xff0c;最好直接斷電&#xff0c;進入…
閱讀更多...
5-數據結構-數組的學習

5-數據結構-數組的學習

5.1數組的定義 定義&#xff1a; 由一組類型相同的數據元素構成的有序集合&#xff0c;每個數據元素稱為一個數據元素&#xff08;簡稱元素&#xff09;&#xff0c;每個元素受n&#xff08;n>1&#xff09;個線性關系的約束&#xff0c;每個元素在n個線性關系中的序號i1、…
閱讀更多...
timm 視覺庫中的 create_model 函數詳解

timm 視覺庫中的 create_model 函數詳解

timm 視覺庫中的 create_model 函數詳解 最近一年 Vision Transformer 及其相關改進的工作層出不窮&#xff0c;在他們開源的代碼中&#xff0c;大部分都用到了這樣一個庫&#xff1a;timm。各位煉丹師應該已經想必已經對其無比熟悉了&#xff0c;本文將介紹其中最關鍵的函數之…
閱讀更多...
C--數據結構--樹的學習

C--數據結構--樹的學習

6.2.1二叉樹的性質 1.二叉樹 性質&#xff1a; 1.若二叉樹的層次從1開始&#xff0c;則在二叉樹的第i層最多有2^(i-1)個結點 2.深度為k的二叉樹最多有2^k -1個結點 &#xff08;k>1&#xff09; 3.對任何一顆二叉樹&#xff0c;如果其葉結點個數為n0,度為2的非葉結點個數…
閱讀更多...
TVM：使用 Schedule 模板和 AutoTVM 來優化算子

TVM：使用 Schedule 模板和 AutoTVM 來優化算子

TVM&#xff1a;使用 Schedule 模板和 AutoTVM 來優化算子 在本文中&#xff0c;我們將介紹如何使用 TVM 張量表達式&#xff08;Tensor Expression&#xff0c;TE&#xff09;語言編寫 Schedule 模板&#xff0c;AutoTVM 可以搜索通過這些模板找到最佳 Schedule。這個過程稱為…
閱讀更多...
TVM：使用 Auto-scheduling 來優化算子

TVM：使用 Auto-scheduling 來優化算子

TVM&#xff1a;使用 Auto-scheduling 來優化算子 在本教程中&#xff0c;我們將展示 TVM 的 Auto-scheduling 功能如何在無需編寫自定義模板的情況下找到最佳 schedule。 與基于模板的 AutoTVM 依賴手動模板定義搜索空間不同&#xff0c;auto-scheduler 不需要任何模板。 用…
閱讀更多...
C語言—sort函數比較大小的快捷使用--algorithm頭文件下

C語言—sort函數比較大小的快捷使用--algorithm頭文件下

sort函數 一般情況下要將一組數從的大到小排序或從小到大排序&#xff0c;要定義一個新的函數排序。 而我們也可以直接使用在函數下的sort函數&#xff0c;只需加上頭文件&#xff1a; #include<algorithm> using namespace std;sort格式&#xff1a;sort(首元素地址&…
閱讀更多...
散列的使用

散列的使用

散列 散列簡單來說&#xff1a;給N個正整數和M個負整數&#xff0c;問這M個數中的每個數是否在N中出現過。 比如&#xff1a;N&#xff1a;{1,2,3,4}&#xff0c;M{2,5,7}&#xff0c;其中M的2在N中出現過 對這個問題最直觀的思路是&#xff1a;對M中每個欲查的值x&#xff0…
閱讀更多...
關于C++中的unordered_map和unordered_set不能直接以pair作為鍵名的問題

關于C++中的unordered_map和unordered_set不能直接以pair作為鍵名的問題

關于C中的unordered_map和unordered_set不能直接以pair作為鍵名的問題 在 C STL 中&#xff0c;不同于有序的 std::map 和 std::set 是基于紅黑樹實現的&#xff0c;std::unordered_map 和 std::unordered_set 是基于哈希實現的&#xff0c;在不要求容器內的鍵有序&#xff0c…
閱讀更多...
最新文章

Copyright @ 2022~2023