checkbox wpf 改變框的大小_【論文閱讀】傾斜目標范圍框(標注)的終極方案

前言

最常用的斜框標注方式是在正框的基礎上加一個旋轉角度θ，其代數表示為(x_c,y_c,w,h,θ)，其中(x_c,y_c )表示范圍框中心點坐標，(w,h)表示范圍框的寬和高[1,2,7]。對于該標注方式，如果將w和h的值互換，再將θ加上或者減去2kπ+π?2，就能夠表示同一個范圍框。由于同一個范圍框有多種不同的數值表示，會導致近似范圍框之間的數值差異有大大小小多種情況。如果近似范圍框之間的數值差異大，對于基于監督分類的方法來說，就是損失函數的取值異常[7]，不利于模型訓練。此標注方式還有一種變形，標注正框時不是記錄寬和高，而是記錄中心點到四邊的距離[6]，當然同樣會有損失異常的問題。

記錄四個頂點的坐標也可以用于標注斜框，武大夏桂松和華科白翔團隊制作的DOTA[4]數據集以及中國科學院大學模式識別與智能系統開發實驗室標注的UCAS-AOD[5]數據集就采用了這種標注方式。由于可以從四個頂點中的任意一個開始記錄，此標注方式導致同一個范圍框有多種不同的數值表示，進而會導致損失異常[7]，增加回歸難度，不利于模型訓練。避免損失異常的現行方式是按照坐標值排序頂點，然后計算對應坐標點之間的差異。這種處理方式也是有問題的，對坐標值排序會改變數值維度間的對應關系[8, 9]，也就是說，在某次損失計算過程中預測向量的第一維對應真值向量的第二維，在另外一次損失計算過程中第一維可能對應第三維。這種對應關系的隨機性同樣不利于模型訓練。記錄四個頂點坐標的好處是可以表示任意四邊形，但是在表示矩形時會有三個冗余量。一種去除冗余的方式是按順時針順序記錄矩形四個頂點中的前兩個和第二個頂點到第三個頂點的距離[7]，但是同樣會出現一個范圍框有多種不同的數值表示。

還有一種斜框標注方式是記錄斜框的外接正框以及斜框四個頂點與正框四個頂點順時針方向的偏移量[8]。該標注方式同樣可以表示任意四邊形，如果只記錄斜框量個頂點與正框兩個頂點順時針方向的偏移量就只能表示矩形框[9]。目前沒有用該標注方式標注樣本的，而是用于先預測正框再進一步預測真實的斜框，在預測正框時將錨點框向斜框的外接正框回歸。但是要想斜框預測得準確就要求正框也得預測準確，增加了預測目標數量，也就增加了回歸難度，同樣不利于模型訓練。

本文提供了一種矩形斜框標注方式，可以用作樣本標注和模型的回歸目標。該標注方式沒有冗余量，同一個范圍框只有一種數值表示，作為回歸目標時不會出現損失異常，有利于模型訓練。本文還將此標注方式與多種其他傾斜范圍框標注方式在目標檢測任務上進行了對比驗證。對比實驗證明此標注方式對于朝向任意、密集排布的目標檢測具有一定的優勢。

標注方法

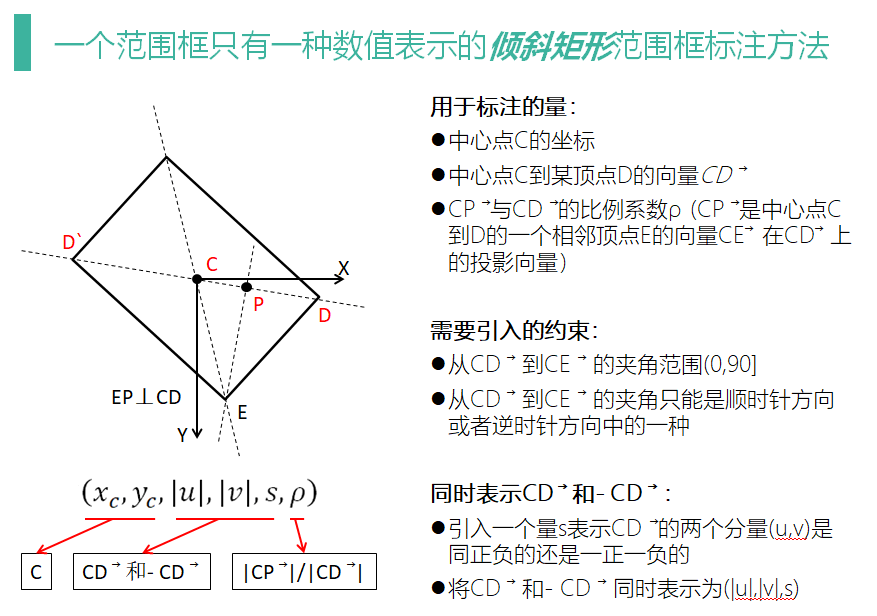
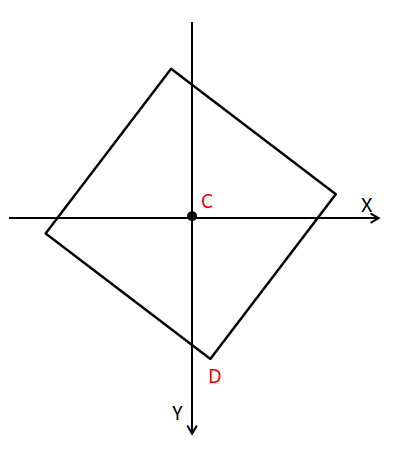
本文提供的斜框標注方式用于標注的量有“中心點C的坐標、中心點到任意一個頂點D的向量□((CD) ? )、C到D的一個相鄰頂點E的向量□((CE) ? )在□((CD) ? )上的投影向量□((CP) ? )與□((CD) ? )的比例系數”，代數表示為(x_c,y_c,u,v,ρ)，其中(x_c,y_c )為中心點C的坐標，(u,v)為向量□((CD) ? )的坐標，ρ為向量□((CP) ? )與□((CD) ? )的比例系數。

圖1中黑實線表示傾斜范圍框，X表示表示圖像行方向上的坐標軸，Y表示圖像列方向上的坐標軸，C表示范圍框的中心點，D、E為范圍框的某兩個頂點，P為□((CE) ? )在□((CD) ? )上的投影點。

由于向量□((CD) ? )可以從四個中任取，□((CE) ? )向量可以從兩個中任取，必須提供一些外在約束確保標注方式數值表示的唯一性。首先，要求ρ的取值范圍為[0,1) ，也就是□((CP) ? )與□((CD) ? )同向；另外要求從□((CD) ? )到□((CE) ? )的夾角只能是順時針方向或者逆時針方向中的一種。

圖1-用于標注范圍框的量有中心點C、向量□((CD) ? )、□((CP) ? )與□((CD) ? )的比例系數

如此一來，同一個范圍框只有兩種數值表示。也就是說，將向量□((CD) ? )取反，但保持其它值不變，仍然表示同一個范圍框。由于同一個范圍框的兩種表示之間只有向量(CD) ?是相反的，可以引入一個量s表示(CD) ?的兩個分量是同正負的還是一正一負的（后文將稱之為同號或異號，可見s只有兩種取值），那么可以用(|u|,|v|,s)表示(CD) ?和-(CD) ?。同號時，(CD) ?和-(CD) ?分別為(|u|,|v| )和(-|u|,-|v| )；異號時，(CD) ?和-(CD) ?分別為(-|u|,|v| )和(|u|,-|v| )。此時就可以將同一個范圍框的數值表示減少到一個，其代數表示為(x_c,y_c,|u|,|v|,s,ρ)。

從圖1中還可以看出，如果是正框，顯然向量(CD) ?的坐標就是范圍框寬高的一半。可以通過令(u,v)=2(CD) ?使該標注方式與正框的相應標注方式兼容。

求解頂點坐標和邊長

在給定標注數值(x_c,y_c,|u|,|v|,s,ρ)時，向量□((CD) ? )就是已知的，向量□((CP) ? )可以表示為□(ρ(CD) ? )。那么要獲得范圍框四個頂點的坐標，將引入的外部約束用方程進行表示，通過求解以下方程組的實現。

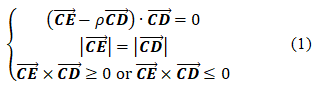
方程組中的第一個式子表示向量□((EP) ? )與向量□((CD) ? )垂直，第二個式子表示向量□((CP) ? )與向量□((CD) ? )的長度相等，第三個式子表示從□((CD) ? )到□((CE) ? )的夾角只能是順時針方向或者逆時針方向中的一種。第三個式子只取用一個即可。

范圍框的邊長可以用下式計算。

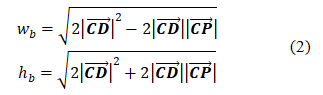
式中w_b是范圍框的短邊長度，h_b是范圍框的長邊長度。

正方形范圍框

易知，在范圍框是正方形時，即使滿足前述約束條件，仍然有兩種數值表示。取任意一個頂點作為參考向量□((CD) ? )，中心點到其順時針或逆時針方向的相鄰頂點的向量在□((CD) ? )上的投影總是0。如果ρ的取值不允許為0，就不能表示正方形范圍框，雖然正方形范圍框非常少見。

我們解決方案是，為正方形范圍框引入額外的約束：□((CD) ? )與X軸夾角的取值范圍為[ 0,90) 度。這這個約束條件下，□((CD) ? )只能落在X軸上或者第一、三象限。

圖2 正方形范圍框

s的損失平滑

圖3中實線和虛線范圍框的s值不同，但是它們卻是非常近似的范圍框。因此s值的差異不能真實體現范圍框之間的差異。容易看出，□((CD) ? )與坐標軸的夾角越小，s的差異越是不能真實體現范圍框之間的差異。

圖3 s值不同，但是它們卻是非常近似的范圍框

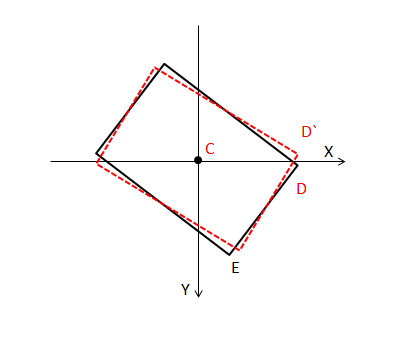
□((CD) ? )與坐標的夾角越小，□((CD) ? )的兩個分量的模之間的差異越大。當□((CD) ? )的兩個分量的模之間的差異大到一定程度后，為s的差值乘上一個很小的權重來平滑s的差異與范圍框的真實差異間的錯配。

我們首先設計了一個函數用于度量□((CD) ? )的兩個分量的模之間的差異。

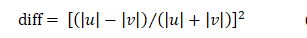
其中|u|,|v|分別是□((CD) ? )的兩個分量的模。可見diff的取值范圍為[0,1]，當|u|,|v|相等時取零，當其中一個為0時取1。在公式(4)中采用了平方函數，實際應用中，為了加快計算速度推薦使用求絕對值函數。然后將diff代入反Sigmoid函數求出s損失的權重。（PS：相減除以相加是常用的評估兩個數量之間相對差異的方式，比如NDVI、NDWI。）

后記

弄這個東西純屬于臨時起意，早些時候為公司做了一個基于深度學習的遙感影像目標檢測軟件，總覺得當時用的范圍框標注方式不夠好。抽了個時間琢磨了一下，設計了這樣一種標注方法。先寫好了專利，覺得把時間投入到深度學習里純屬于浪費生命，問了幾個人是否愿意參與進來做個實驗，我來寫個論文，一作讓出去；然而他們不是沒空，就是水平沒到。

這個標注方式確實還有點價值，不想給埋沒了，只得自己動手，設計了一個目標檢測網絡，在一些數據集上初步試驗了效果，寫了論文的初稿。恰好用了一個月的時間，下面那個分割算法倉庫的提交日志記錄下來了時間，2-15到3-15。

最終論文會發表到國內某個學報上。發論文不是目的，都是先寫專利，論文從專利說明書改出來的。專利說明書中文寫的，也不想翻譯，發中文期刊省事。

這里僅介紹了范圍框標注方式，正式發表的論文里還包含了一個用于對比驗證這個標注方式的網絡，還有一些試驗數據和結論。關于那個目標檢測網絡沒啥好說的，結構簡單不新奇。有了這個標注方式，諸位可以輕松想到，或者想到更好的。另外……

神經網絡的結構有啥好說的

論文出來之后，代碼將會公開到tgis-top/TRD。

引用

[1] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. Faster r-cnn: towards real-time object detection with region proposal networks. In IEEE Transactions on Pattern Analysis and Machine Intelligence, (6):1137–1149, 2017.

[2] Joseph Redmon, Santosh Divvala, Ross Girshick and Ali Farhadi. You only look once: Unified, real-time object detection. In Proc. of CVPR, p779–788, 2016.

[3] Wei Liu, Dragomir Anguelov, Dumitru Erhan, Christian Szegedy, Scott Reed, Cheng-Yang Fu, and Alexander C Berg. Ssd: Single shot multibox detector. In ECCV, p21–37. Springer, 2016.

[4] Gui-Song Xia, Xiang Bai, Jian Ding, Zhen Zhu, Serge Belongie, Jiebo Luo, Mihai Datcu, Marcello Pelillo, and Liangpei Zhang. DOTA: A Large-scale Dataset for Object Detection in Aerial Images. In CVPR, 2018.

[5] Haigang Zhu, Xiaogang Chen, Weiqun Dai, Kun Fu, Qixiang Ye, Jianbin Jiao. Orientation Robust Object Detection in Aerial Images Using Deep Convolutional Neural Network. IEEE Int'l Conf. Image Processing, 2015.

[6] Xinyu Zhou, Cong Yao, He Wen, Yuzhi Wang, Shuchang Zhou, Weiran He, and Jiajun Liang. East: an efficient andaccurate scene text detector. In Proc. CVPR, p2642–2651, 2017.

[7] Yingying Jiang, Xiangyu Zhu, Xiaobing Wang, Shuli Yang,Wei Li, Hua Wang, Pei Fu, and Zhenbo Luo. R2cnn: rotational region cnn for orientation robust scene text detection. arXiv:1706.09579, 2017.

[8] Xue Yang,Jirui Yang, Junchi Yan, Yue Zhang, Tengfei Zhang, Zhi Guo, Sun Xian, and Kun Fu. SCRDet: Towards More Robust Detection for Small, Cluttered and Rotated Objs. In ICCV, 2019.

[9] Yongchao Xu, Mingtao Fu, Qimeng Wang, Yukang Wang, Kai Chen, Gui-Song Xia, and Xiang Bai. Gliding vertex on the horizontal bounding box for multi-oriented obj detection. arXiv:1911.09358, 2019.

[10] Youtian Lin, Pengming Feng, and Jian Guan. IENet: Interacting Embranchment One Stage Anchor Free Detector for Orientation Aerial Object Detection. arXiv:1912.00969, 2019.

[11] Tsung-Yi Lin, Piotr Doll ?ar, Ross B Girshick, Kaiming He, Bharath Hariharan, and Serge J Belongie. Feature pyramid networks for object detection. In Proc. of CVPR, vol 1, page 4, 2017.

[12] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proc. of CVPR, pages 770–778, 2016.