徹底理解BP之手寫BP圖像分類你也行
轉自:https://zhuanlan.zhihu.com/p/397963213
第一節:用矩陣的視角,看懂BP的網絡圖
1.1、什么是BP反向傳播算法
- BP(Back Propagation)誤差反向傳播算法,使用反向傳播算法的多層感知器又稱為BP神經網絡。BP是當前人工智能主要采用的算法,例如你所知道的CNN、GAN、NLP中的Bert、Transformer,都是BP體系下的算法框架。
- 理解BP對于理解網絡如何訓練很重要
- 在這里我們采用最簡單的思路理解BP。確保能夠理解并且復現
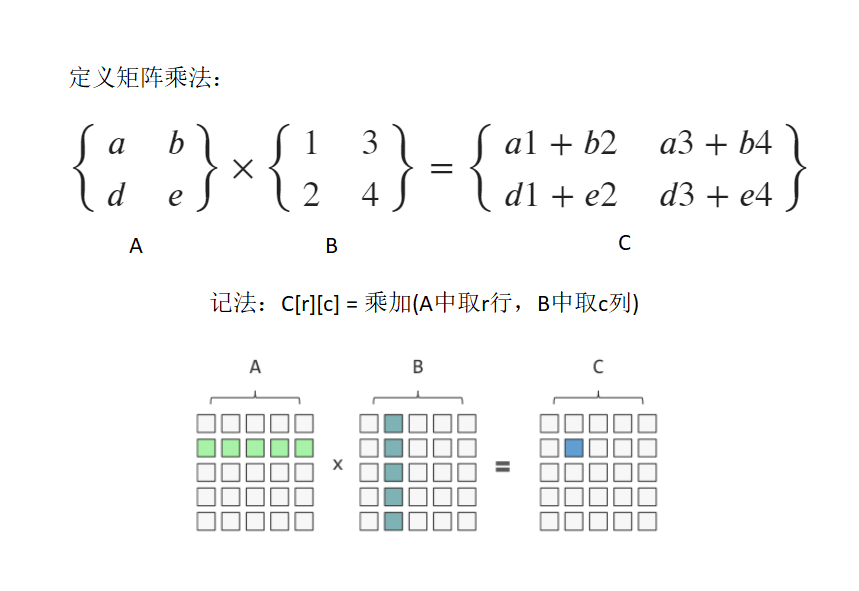
1.2、矩陣乘法
- 參考:https://www.cnblogs.com/ljy-endl/p/11411665.html
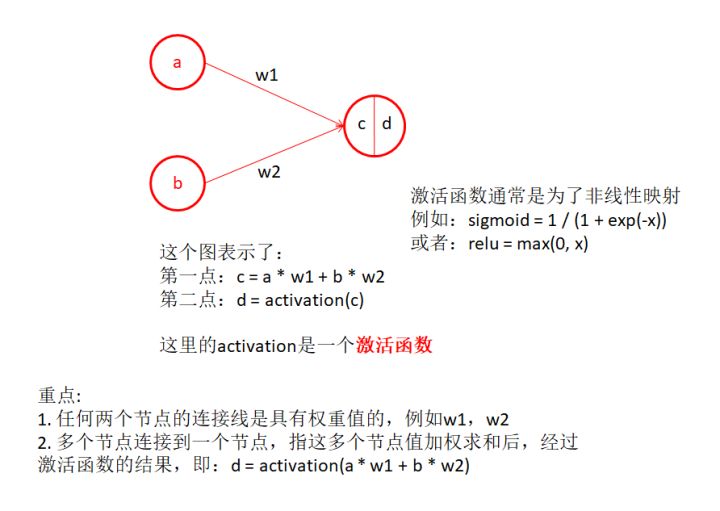
1.3、感知機
- 感知機模擬了神經元突觸的信息傳遞
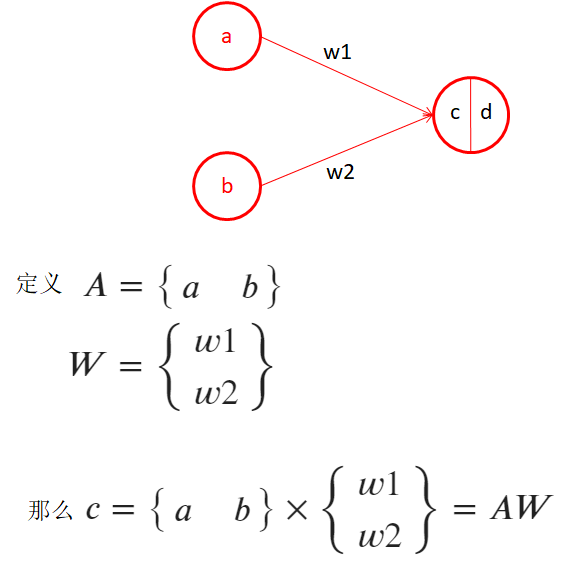
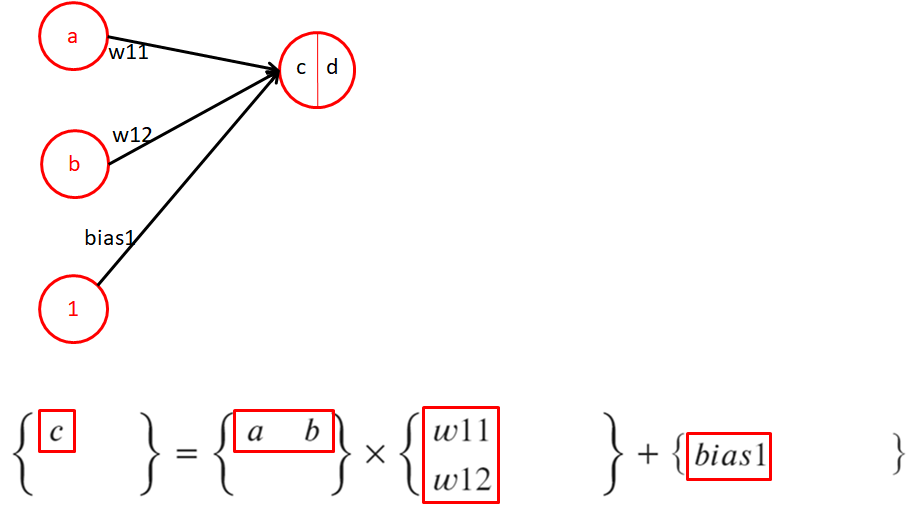
1.4、感知機-矩陣表示
- 用矩陣的視角來定義感知機結構
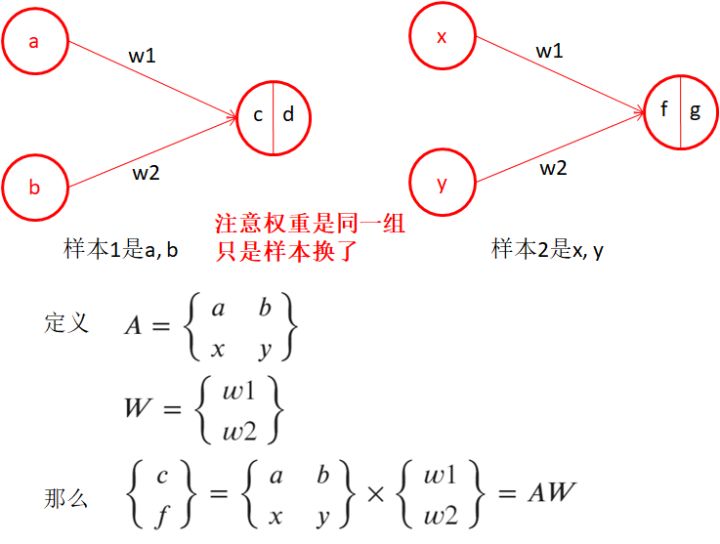
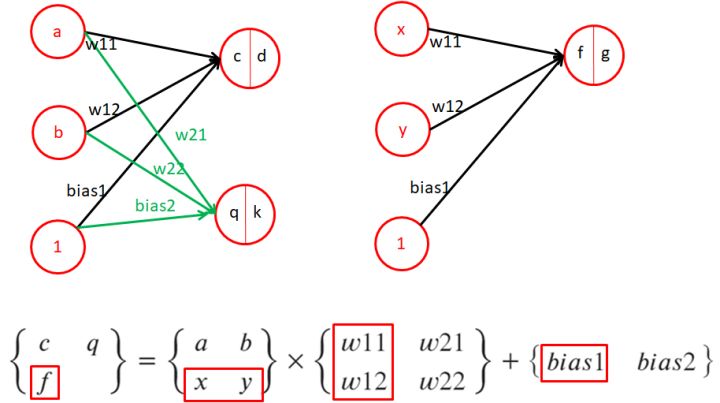
1.5、感知機-多個樣本
- 當a、b是第一個,x、y是第二個樣本時
1.6、感知機-增加偏置
- 關于偏置的存在,考慮y = kx + b直線公式,若b=0,則退化為y = kx,此時表達的直線必定過0點,無法表達不過0點的直線,所以偏置在這里非常重要
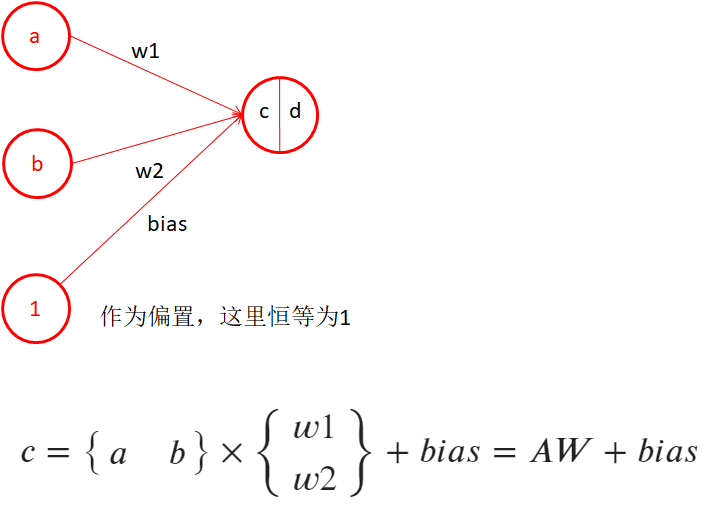
1.7、感知機-多個樣本,并增加偏置(樣本維度增加)
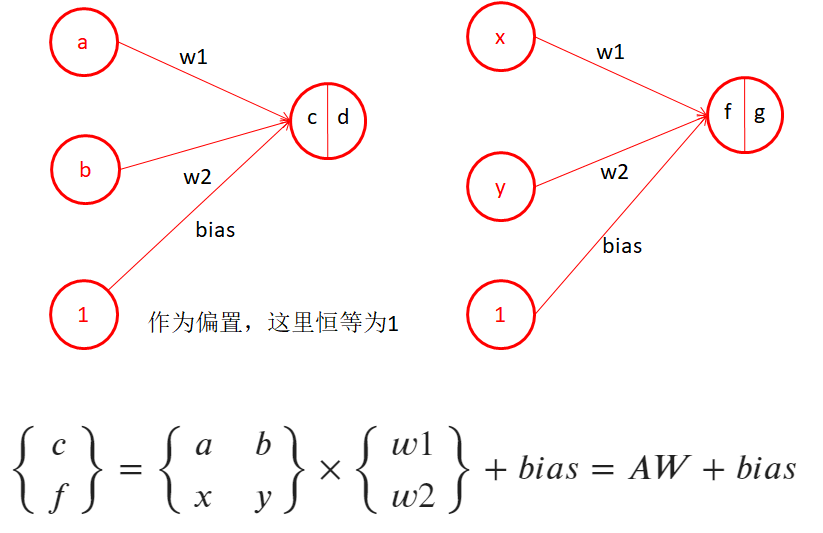
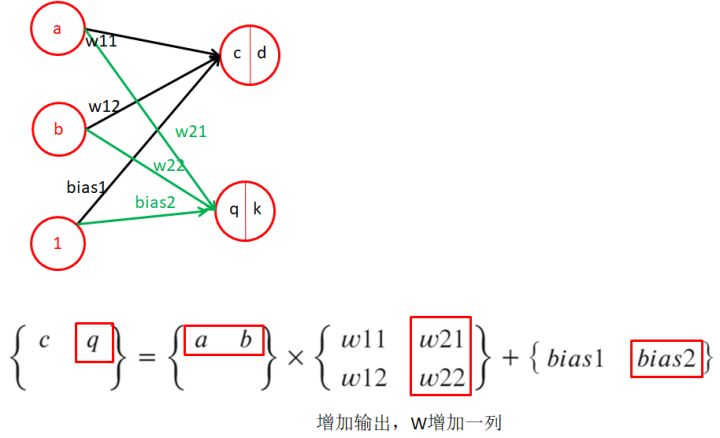
1.8、感知機-多個輸出,同一個樣本(輸出維度增加)
- 討論增加一個輸出時的樣子
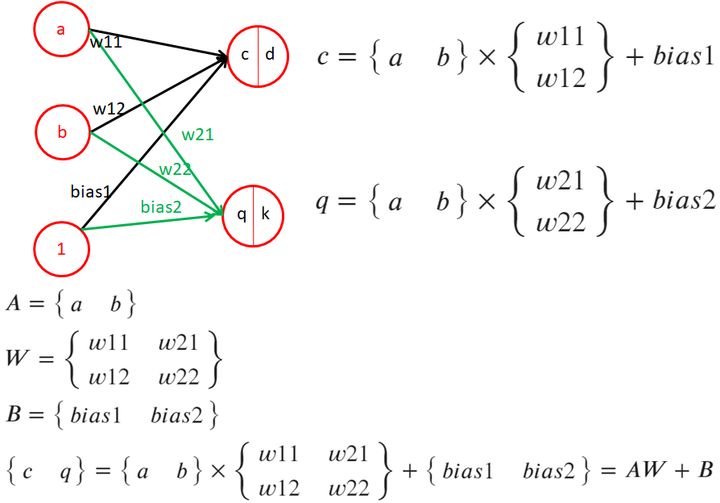
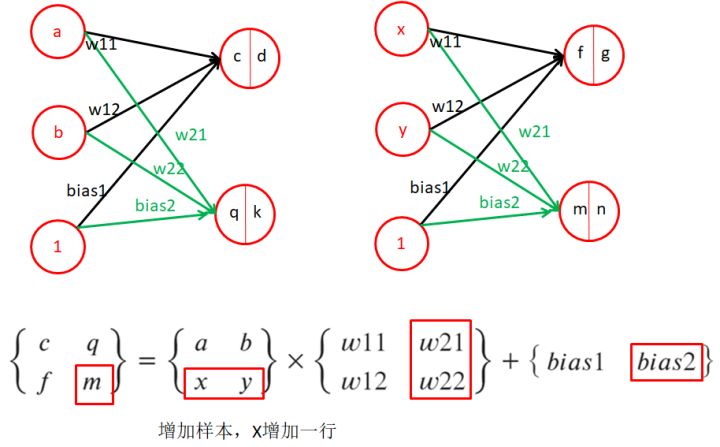
1.9、感知機-多個樣本,多個輸出(樣本、輸出維度同時增加)
- 當樣本維度,和輸出維度同時增加時
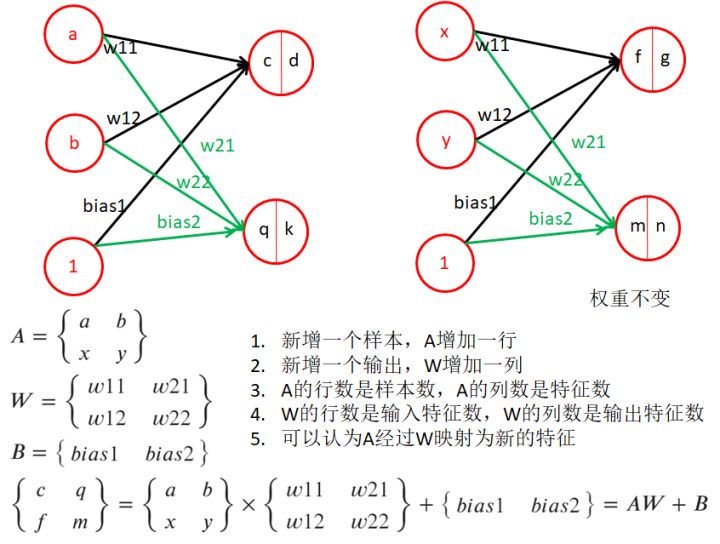
1.10、關于廣播機制
- 對于矩陣A和B的元素操作(點乘、點加、點除等等)。廣播機制約定了,假設A是1x5,B是3x5,則約定把A在行方向復制3份后,再與B進行元素操作,同理可以發生在列上,或發生在B上

1.11、以下是動畫
- 解釋維度增加時,矩陣表示的差異
1.12、鍛煉一下
- 注意這里沒有考慮激活的存在
- 是否和你想的一樣?
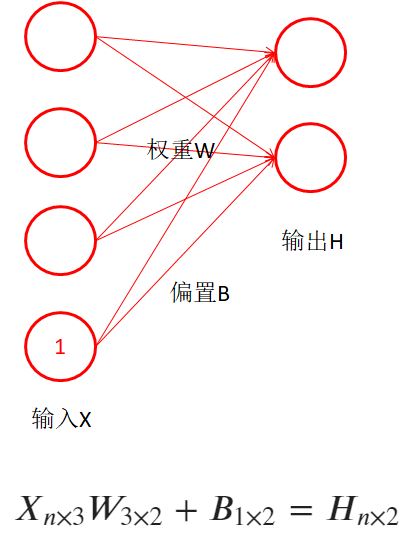
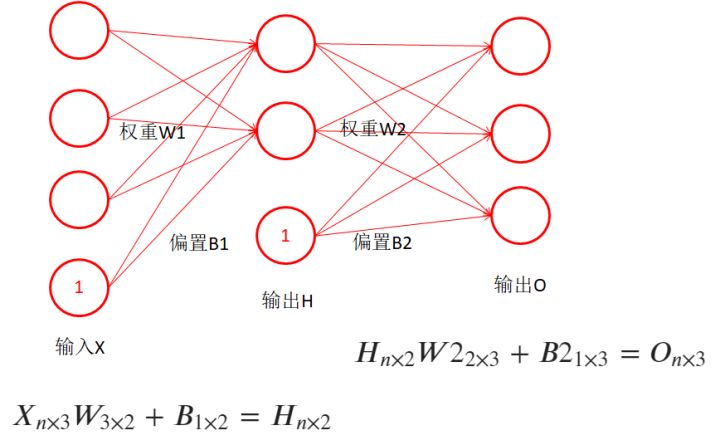
- 再回過頭看BP的圖,你看懂了嗎?學會了用矩陣的視角看這種了嗎?
- 這種圖通常省略了偏置和激活,實際中都存在偏置和激活
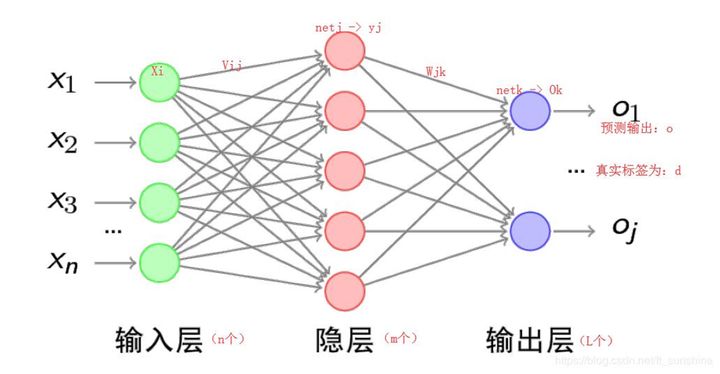
第二節:BP在干嘛,到,函數的最小化
- BP到底干了嘛,函數最小化是什么?
2.1 實際例子,理解樣本書、特征數
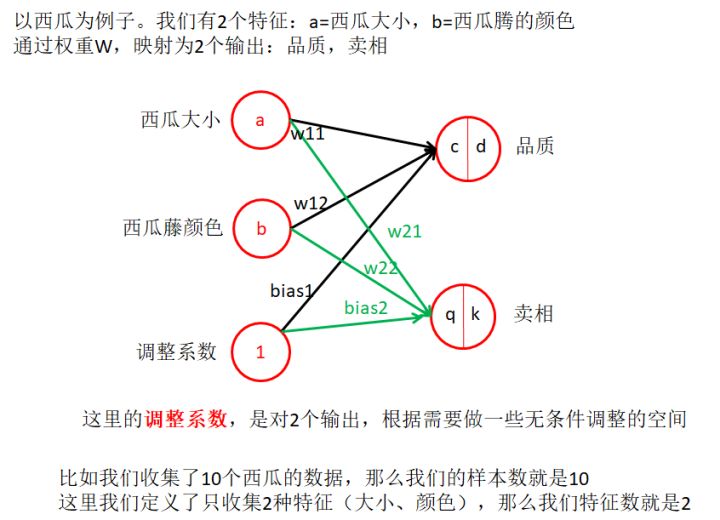
2.2 理解BP的意義
- 當我們明白了,特征可以逐層映射到結論時,輸入特征和結論可以收集得到。權重該怎么來呢?對,BP就是在給定輸入特征和輸出結論后,告訴你中間權重應該取值多少是合適的
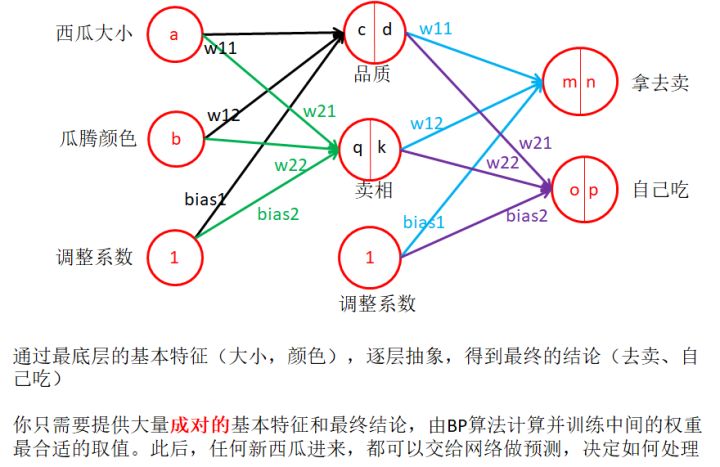
2.3 樣本1
- 這里分析了單位帶來的問題
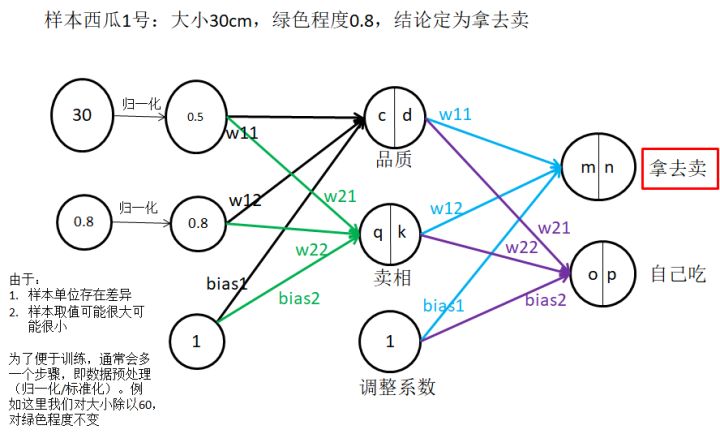
2.4 樣本2
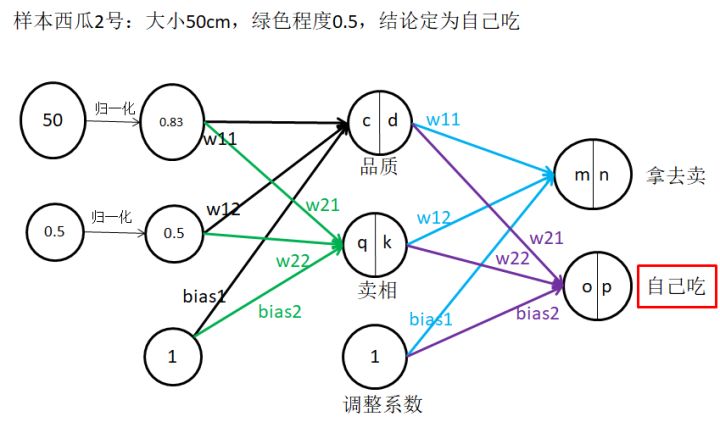
2.5 發生誤差
- 這里著重強調輸入特征、推測結果、結論之間的關系
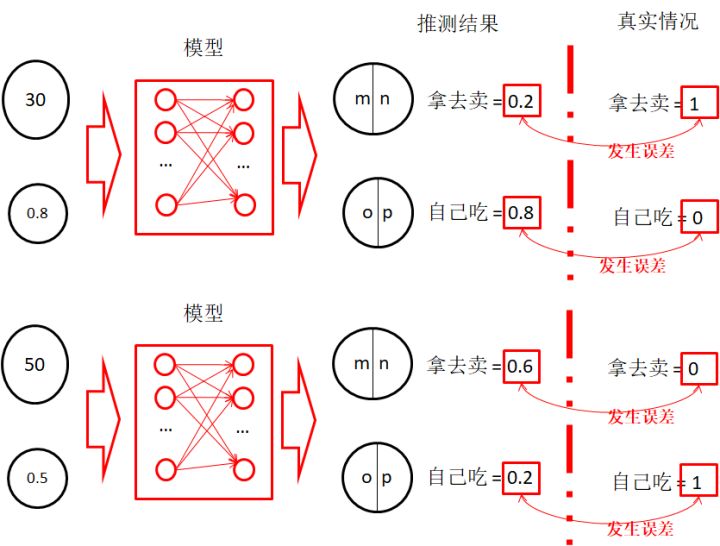
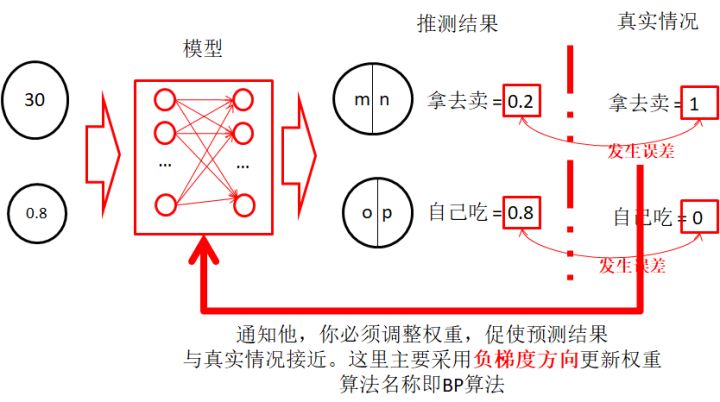
- 通過推測結果和真實情況之間的誤差,反向傳遞到模型中,促使模型做出調整,使得推測結果更接近真實情況。用到的方法即誤差反向傳播算法(BP,Back Propagation)
2.6 定義誤差度量方式
- 注意,分類問題二元交叉熵更合適,這里為了簡化
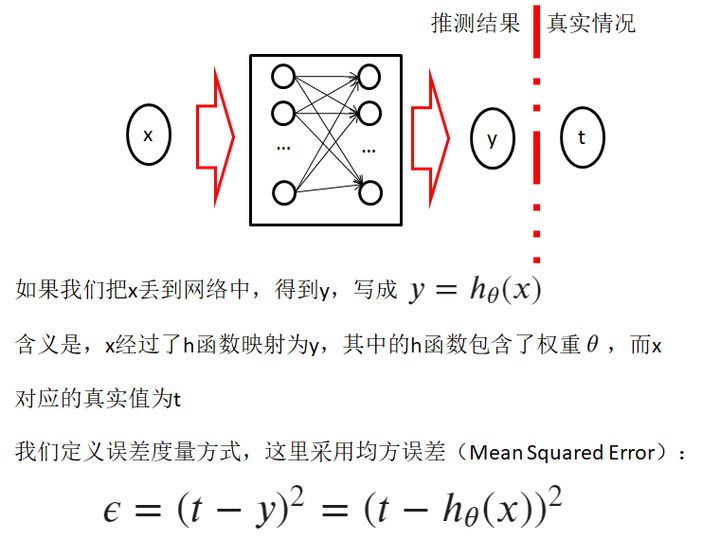
2.7 轉換為函數最小化問題
- 歸根結底是為了知道誤差最小時, [外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-YuRuTYw4-1657805811986)(https://www.zhihu.com/equation?tex=%5Ctheta)] 的取值,如何得到最合適的權重?
- 這里提到,BP告訴我們,采用 [外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-HfClaXwG-1657805811986)(https://www.zhihu.com/equation?tex=%5Ctheta)] 的負梯度方向,關于負梯度方向,請看后面分析

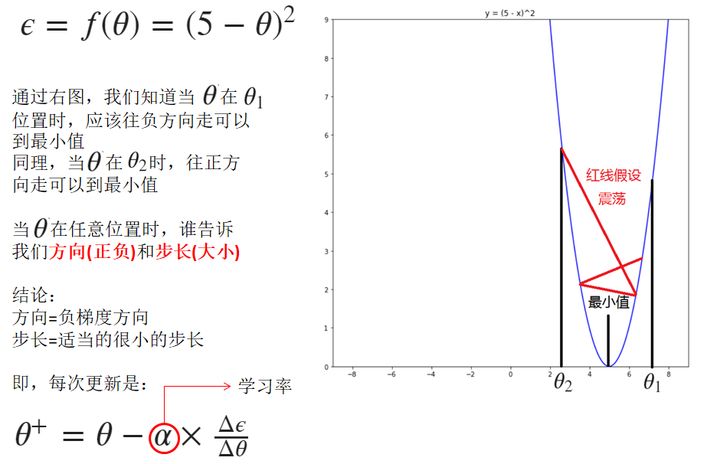
2.8 函數最小化舉例1

2.9 函數最小化舉例2
- 為什么是適當的很小步長,因為梯度方向告訴我們函數上升最快的方向,但是并沒有人告訴我們,距離最小值有多遠,那么我們只能走很小的一步。然后再看看梯度方向,繼續走很小一步。多次迭代后,找到最小值。如果步長太大,其結果是在中間震蕩,無法收斂。所以是超參數,經驗值
第三節:矩陣求導的推導和結論
- 既然BP可以用矩陣描述,那么反向求導時,則需要處理矩陣求導。這是簡化BP理解的一個關鍵,一定不要用單個值的方式去理解他,太繞了,還難以實現
3.1 導數定義
- 資料:https://www.cnblogs.com/lingjiajun/p/9895753.html

3.2 f(x)=ax時的導數

3.3 f(x)=x^2時的導數
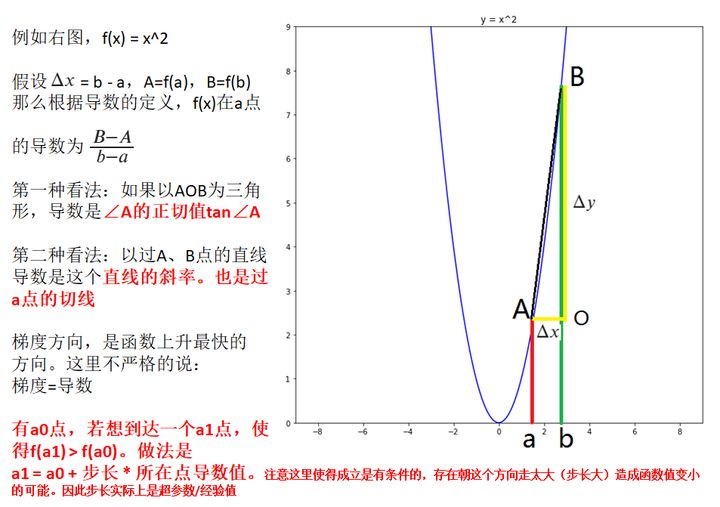
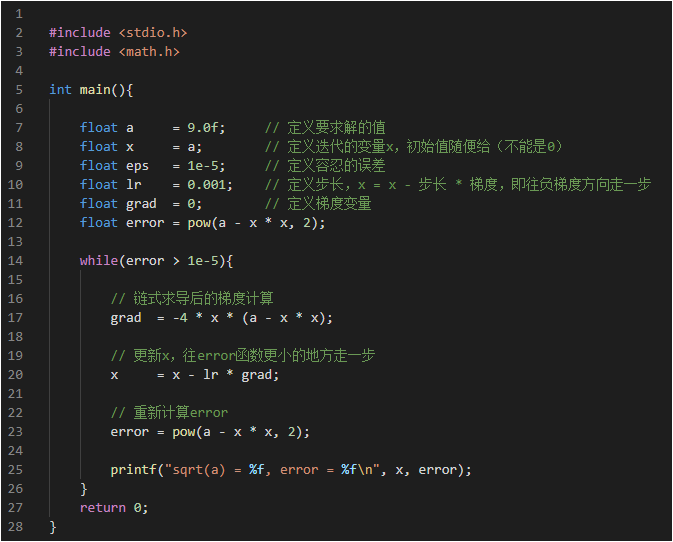
3.4 使用梯度下降求解sqrt(a)

- 有了導數值,我們可以使用梯度下降(負梯度方向更新)法,迭代找到誤差函數的極小值位置,今兒找到我們想要的解
- 步驟如下:

- 代碼部分如下:
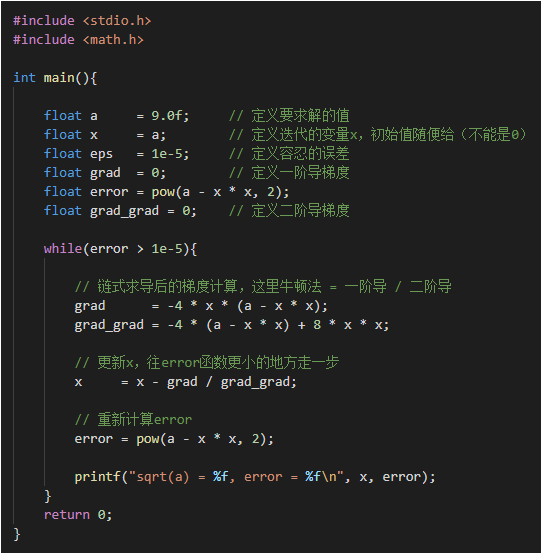
3.5 擴展閱讀,使用牛頓法求解sqrt(a)
- 牛頓法更新時,采用的是x = x - 一階導/二階導,速度比梯度下降法快不少,但是他要求解二階導很難計算
3.6 矩陣求導,定義操作
- 定義基本操作,模擬誤差計算函數,使用矩陣表達
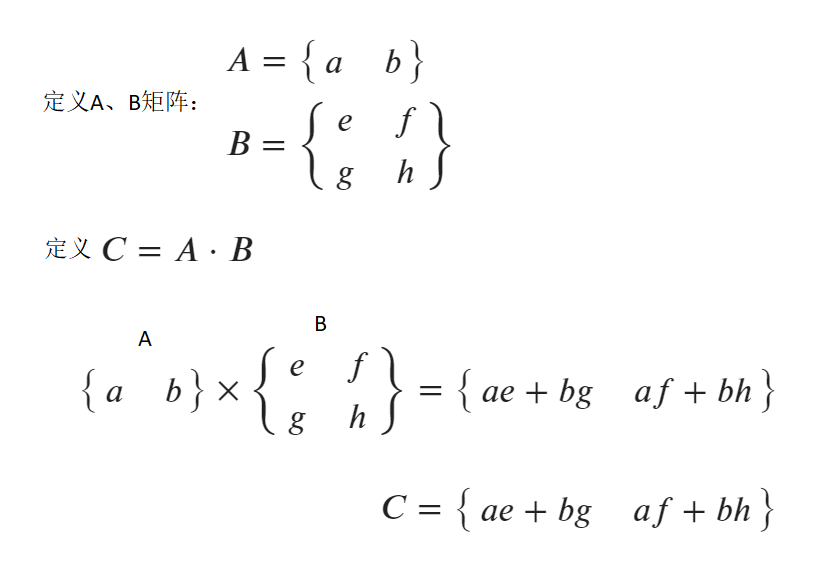
3.7 定義誤差函數error

3.8 匯總error的定義

3.9 error對A的偏導數

3.10 error對B的偏導數

3.11 矩陣求導結論

第四節:代碼實現
4.1 介紹
- 對于C++
- 既然是基于矩陣操作,則首先要實現基于C++的矩陣類。這里matrix.hpp解決矩陣操作問題(矩陣的元素操作、廣播等)
- 由于C++矩陣乘法效率問題,可以考慮引用OpenBLAS庫
- 工程實現代碼請訪問:https://github.com/shouxieai/bp-cpp
- 對于Python
- 直接利用Numpy可以輕易實現矩陣操作、廣播、元素乘法
- Python中Numpy的矩陣操作,已經進行了優化
IDE采用VSCode,編譯采用Makefile,若要配置Makefile和vscode的開發環境,請訪問:使用Makefile配置標準工程環境
4.2 圖像矩陣化
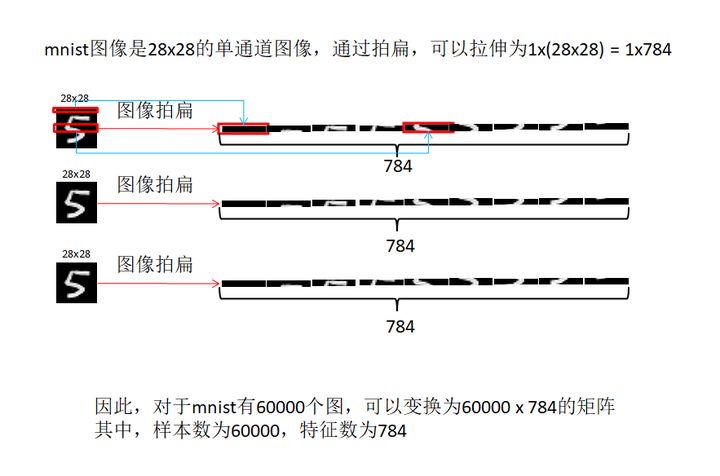
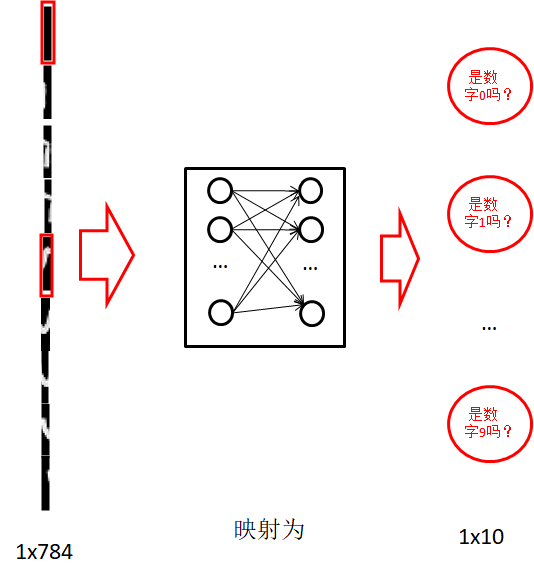
4.3 訓練邏輯
- 加載mnist數據集為矩陣,分別有:
- 訓練集圖像:50000 x 784
- 訓練集標簽:50000 x 1
- 測試集圖像:10000 x 784
- 測試集標簽:10000 x 1
\2. 預處理數據
-
- 將訓練集圖像轉換為浮點數,并做歸一化
- 將訓練集標簽轉換為onehot熱獨編碼,變為50000 x 10
- 將測試集圖像轉換為浮點數,并做歸一化
- 將測試集標簽轉換為onehot熱獨編碼,變為10000 x 10
- 將訓練集圖像轉換為浮點數,并做歸一化
\3. 初始化部分
-
-
初始化超參數,隱藏層數量定為1024,迭代次數10輪,動量0.9,批次大小256
-
定義4個權重,分別是
-
- 輸入映射到隱層(input_to_hidden):784 x 1024
- 隱層偏置(hidden_bias):1 x 1024
- 隱層到輸出層(hidden_to_output):1024 x 10
- 輸出層偏置(output_bias):1 x 10
- 輸入映射到隱層(input_to_hidden):784 x 1024
-
初始化權重,使用凱明初始化fan_in + fan_out,偏置初始化為0
-
-
\4. 前向部分 - forward
-
-
從訓練集中,隨機選擇batch個樣本記為x(batch x 784)。選擇對應的onehot標簽記為y(batch x 10)
-
以x乘以映射矩陣(input_to_hidden),然后加上隱層偏置,再對結果做激活。作為隱層輸出,這里采用relu函數為激活
-
- hidden_act = (x @ input_to_hidden + hidden_bias).relu()
-
以hidden_act乘以映射矩陣(hidden_to_output),然后加上輸出層偏置,再對結果做激活。作為輸出層的輸出值。這里采用sigmoid函數做激活
-
- probability = (hidden_act @ hidden_to_output + output_bias).sigmoid()
-
使用probability和y計算交叉熵損失,并打印損失
-
-
\5. 反向部分 - backward
-
- 計算loss對所有權重的梯度,例如先計算對括號內的導數,然后鏈式求導往前遞推直至所有權重梯度計算出來,這里利用矩陣求導
- 對所有權重,和其梯度值,執行SGDMomentum算法更新權重。該算法相比前面講的增加了動量因素。稍微公式不一樣
- 計算loss對所有權重的梯度,例如先計算對括號內的導數,然后鏈式求導往前遞推直至所有權重梯度計算出來,這里利用矩陣求導
\6. 循環迭代,直至迭代次數滿足定義次數后結束并儲存模型
PPT課件下載
點擊下載
原稿地址
徹底理解,BP反向傳播算法,矩陣思維你更好懂 | 手寫AI
視頻講解
崔更,規劃中,B站主頁地址:https://space.bilibili.com/1413433465/



















)