? 定義
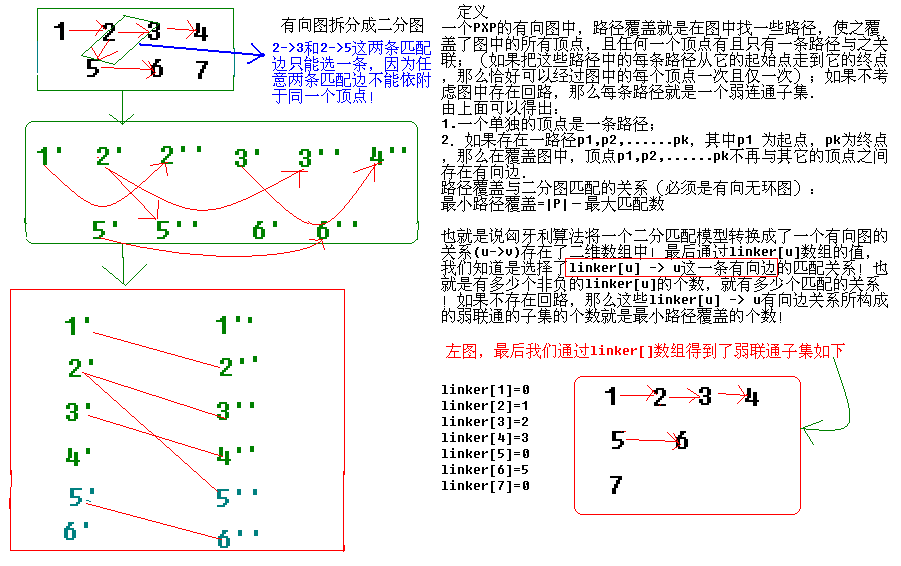
一個PXP的有向圖中,路徑覆蓋就是在圖中找一些路徑,使之覆蓋了圖中的所有頂點,且任何一個頂點有且只有一條路徑與之關聯;(如果把這些路徑中的每條路徑從它的起始點走到它的終點,那么恰好可以經過圖中的每個頂點一次且僅一次);如果不考慮圖中存在回路,那么每條路徑就是一個弱連通子集.
由上面可以得出:
1.一個單獨的頂點是一條路徑;
2.如果存在一路徑p1,p2,......pk,其中p1 為起點,pk為終點,那么在覆蓋圖中,頂點p1,p2,......pk不再與其它的頂點之間存在有向邊.
路徑覆蓋與二分圖匹配的關系(必須是有向無環圖):
最小路徑覆蓋=|P|-最大匹配數
也就是說匈牙利算法將一個二分匹配模型轉換成了一個有向圖的關系(u->v)存在了二維數組中!最后通過linker[u]數組的值,我們知道是選擇了linker[u] -> u這一條有向邊的匹配關系!也就是有多少個非負的linker[u]的個數,就有多少個匹配的關系!如果不存在回路,那么這些linker[u] -> u有向邊關系所構成的弱聯通的子集的個數就是最小路徑覆蓋的個數!
?
?
)




)


...)

)

)




)

)