題目：

打靶

小明參加X星球的打靶比賽。

比賽使用電子感應計分系統。其中有一局，小明得了96分。

這局小明共打了6發子彈，沒有脫靶。

但望遠鏡看過去，只有3個彈孔。

顯然，有些子彈準確地穿過了前邊的彈孔。

不同環數得分是這樣設置的：

1,2,3,5,10,20,25,50

那么小明的6發子彈得分都是多少呢？有哪些可能情況呢？

下面的程序解決了這個問題。

仔細閱讀分析代碼，填寫劃線部分缺失的內容。

public class Main

{

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc)

{

if(ho<0 || bu<0 || sc<0) return;

if(k==ta.length){

if(ho>0 || bu>0 || sc>0) return;

for(int i=0; i

for(int j=0; j

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for(int i=0; i<=bu; i++){

da[k] = i;

f(ta, da, k+1, __________________ , bu-i, sc-ta[k]*i); // 填空位置

}

da[k] = 0;

}

public static void main(String[] args)

{

int[] ta = {1,2,3,5,10,20,25,50};

int[] da = new int[8];

f(ta, da, 0, 3, 6, 96);

}

}注意：只填寫劃線處缺少的內容，不要填寫已有的代碼或符號，也不要填寫任何解釋說明文字等。

本題結論有待驗證，證明后更改，主要糾結于3代表總共三個彈孔，還是三次重復穿過彈孔

如果代表總共三個彈孔 ?答案：i > 0 ?? ho - 1: ho

如果代表總共三次重復穿過：答案：i > 1 ? ho - (i - 1) : ho

分析：

1.main函數分析：

public static void main(String[] args) {

int[] ta = { 1, 2, 3, 5, 10, 20, 25, 50 };//記錄分值

int[] da = new int[8];//記錄每個分值的個數

f(ta, da, k,ho,bu, sc);

f(ta, da, 0, 3, 6, 96);//第一二個參數不用解釋，從ta第0位開始枚舉，3個重復彈孔，上限6個分數，共96分

}

2.遞歸函數分析：

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc) {

if (ho < 0 || bu < 0 || sc < 0)//最后ho bu sc 都大于0 才有遞歸的必要(剪枝)

return;

if (k == ta.length) {// 當k枚舉完ta數組(類似for循環的i)，開始判斷

if (ho > 0 || bu > 0 || sc > 0)// 三個參數都等于0，說明遞歸過程會把已經枚舉的值扣除相應的ho，bu，sc值

return;

for (int i = 0; i < da.length; i++) {//輸出每個分值

for (int j = 0; j < da[i]; j++)

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for (int i = 0; i <= bu; i++) {//bu是分數個數的上限

da[k] = i;//每一個分值從0~bu(即6)進行深搜枚舉

f(ta, da, k + 1, i > 1 ? ho - (i - 1) : ho, bu - i, sc - ta[k] * i); // 填空位置

}

/*剛開始直接填0，發現每個答案加起來就是96，唯一不同的就是，有的彈孔數不是3個

*可見，ho的值就是用來篩選的且要扣除有幾個重復的，由da數組可知每個分值是記錄每個分值個數的

*所以我推出ho,當分值的個數大于1，只要減去每個分值的個數扣掉1之后的值(即重復的數量)，如da[1] = 3,那么我就ho扣掉2

*最后運行，果然，得出了三組數據且只有三個彈孔，完美解決

* */

da[k] = 0;//分值每種情況枚舉完之后要回溯，清零

}

把ho填0，得出的結果：

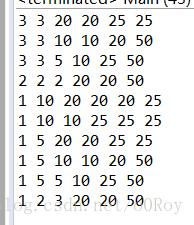
推出代碼后結果：

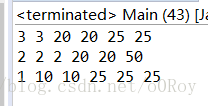
所以應該填入：i > 1 ? ho - (i - 1) : ho

完整代碼：

public class Main {

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc) {

if (ho < 0 || bu < 0 || sc < 0)

return;

if (k == ta.length) {

if (ho > 0 || bu > 0 || sc > 0)

return;

for (int i = 0; i < da.length; i++) {

for (int j = 0; j < da[i]; j++)

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for (int i = 0; i <= bu; i++) {

da[k] = i;

f(ta, da, k + 1, i > 1 ? ho - (i - 1) : ho, bu - i, sc - ta[k] * i); // 填空位置

}

da[k] = 0;

}

public static void main(String[] args) {

int[] ta = { 1, 2, 3, 5, 10, 20, 25, 50 };

int[] da = new int[8];

f(ta, da, k,ho,bu, sc);

f(ta, da, 0, 3, 6, 96);

}

}

總結：

主要還是考深搜還有回溯，跟全排列有點像，類似全排列的進階