
我們比較熟悉的不等式可能就是下面的這個不等式鏈以及柯西不等式了:
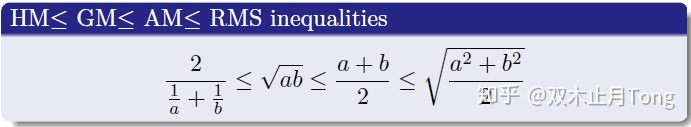

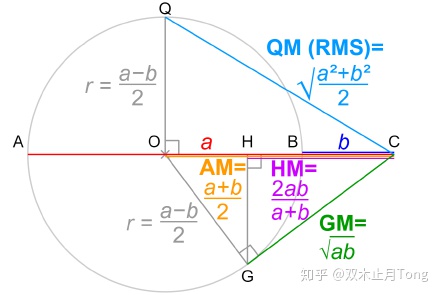
對于不等式鏈的證明我們可以看下面這張圖,非常直觀形象:
不太懂得也可以看這個視頻講解:
知乎視頻?www.zhihu.com對于柯西不等式的證明及講解,我們之前也分享過:
https://zhuanlan.zhihu.com/p/107477843?zhuanlan.zhihu.com今天我們主要是來分享一下三個不太用到的不等式:排序不等式、切比雪夫不等式以及伯努利不等式,接下去我們分別來介紹及證明一下。
一、排序不等式Rearrangement Inequality

之前上課有個學生看到
哈哈,是的,不過這里指的是一個置換,就是把下標(*)換成其它數字。
上面的形式概括一下就是:順序和≥亂序和≥倒序和
接下去證明一下:
【證明】
先證明順序和≥亂序和
假設
如果說
不然,至少存在一個
接著,我們可以分析出來必定存在一個
因為
于是,
也就是說,我們可以通過交換
與假設矛盾,
類似的方法我們也可以用來證明亂序和≥倒序和,大家可以試一下。
放個簡單例題試試手:
Question:
二、切比雪夫不等式Chebyshev's Inequality
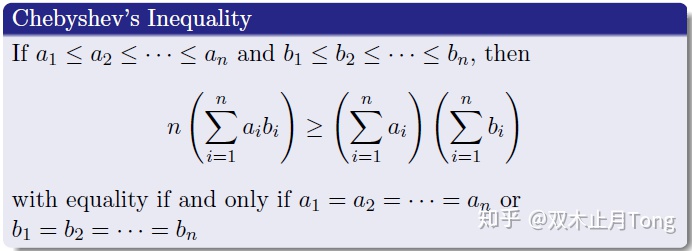
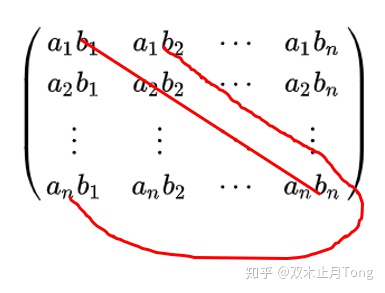
切比雪夫不等式可以通過排序不等式能夠很快得到,不等式左邊是n個順序和,那么不等式的右邊是什么,可能這樣不太直觀,我們把它寫成矩陣形式來看看:
其實是1個順序和+n-1個亂序和,簡單的畫兩條線大家就看清楚了:
三、伯努利不等式Bernoulli's Inequality

可以借助數學歸納法來證明伯努利不等式,下面簡單寫一下:
【證明】
當
假設當
當
因為
下面也給一道關于伯努利不等式的簡單習題,有興趣可以做一下:
Question:
至此,我們就分享完了排序不等式,切比雪夫不等式及伯努利不等式及它們的證明,說實話在國際數學競賽中,比如AMC10/12等,是不太用到的,最重要(最常考)的還是前面的基本不等式以及柯西不等式了。所以,后面的就了解一下,哪天見到了有點印象就可以啦:D
本文就介紹到這里了,歡迎交流指正,感覺還可以的不要忘記點個贊呀!
總感覺干貨好像不太受歡迎?_?
想了解更多國際數學競賽的知識,可參閱:
https://zhuanlan.zhihu.com/p/62918360?zhuanlan.zhihu.com



...)







)


...)


)
)