解題思路:

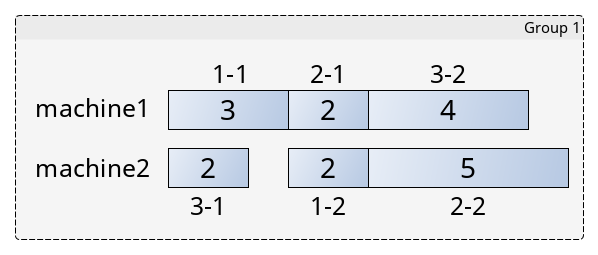
如圖所示，對于第一組樣例輸入，按照總工序提供的順序，對于每個工件的工序從小到大，每次尋找有空閑機器的“空檔”插入，就能讓總加工時間最短。

注意事項:

按照約定，最短方案有且只有一種。

參考代碼:#include

int?w[21];????????????????????????????????????//當前安排的工件處于幾號工序

int?u[501];???????????????????????????????????//安排幾號工件進入總工序

int?lt[21];???????????????????????????????????//當前安排的工件幾時結束

int?t[21][21];????????????????????????????????//每個工件的每個工序的加工時間

int?d[21][21];????????????????????????????????//每個工件的每個工序所使用的機器號

int?c[21][501];???????????????????????????????//每個機器在工件完成后某時間段內是否被占用

int?main(){

int?max(int,int);

int?i,j,k,m,n,ans=0,s=0;

scanf("%d%d",&m,&n);

for(i=1;i<=m*n;i++)?scanf("%d",&u[i]);????//輸入總工序

for(i=1;i<=n;i++)

for(j=1;j<=m;j++)

scanf("%d",&d[i][j]);?????????????//輸入第1個工件第j個工序所使用的機器號

for(i=1;i<=n;i++)

for(j=1;j<=m;j++)

scanf("%d",&t[i][j]);?????????????//輸入第i個工件第j個工序的加工時間

for(i=1;i<=n*m;i++){

w[u[i]]++;????????????????????????????//總工序中第i個工件處于幾號工序

for(j=lt[u[i]]+1;;j++){???????????????//總工序中工件u[i]當前工序若能完成的時間段

if(c[d[u[i]][w[u[i]]]][j]==0)?s++;//工件u[i]在當前工序所使用的機器未被占用時長

else?s=0;

if(s==t[u[i]][w[u[i]]]){??????????//工件u[i]在當前工序的加工時間

for(k=j-s+1;k<=j;k++)?????????//在j之前的這段時間s

c[d[u[i]][w[u[i]]]][k]=1;?//安排工件u[i]在當前工序占用相應的機器

lt[u[i]]=j;???????????????????//工件u[i]的完成時間

s=0;

break;

}

}

}

for(i=1;i<=n;i++)

ans=max(ans,lt[i]);???????????????????//工序中最后一個工件的完成時間

printf("%d",ans);

return?0;

}

int?max(int?a,int?b){

return?a>b?a:b;

}